Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
5th Edition
ISBN: 9781323132098
Author: Thomas, Lay
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.3, Problem 17E
Consider the mouse in the following maze from Section 10.1, Exercise 17.
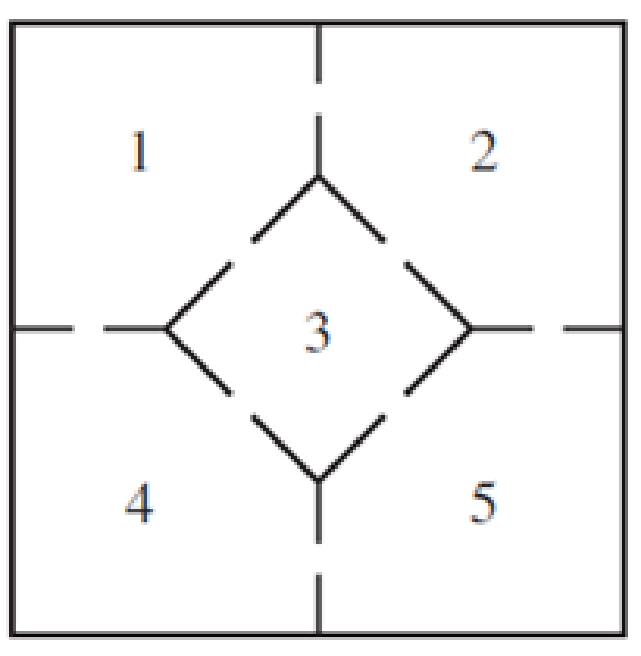
If the mouse starts in room 3, how long on average will it take the mouse to return to room 3?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Monroe County is trying to determine where to place the county fire station. The locations of the county’s four major towns are as follows: (10, 20), (60, 20), (40, 30), and (80, 60) (see Figure 7.50). Town 1 averages 40 fires per year; town 2, 25 fires; town3, 20 fires; and town 4, 30 fires. The county wants to build the fire station in a location that minimizes the average distance that a fire engine must travel to respond to a fire. Because most roads run in either an east-west or a north-south direction, the fire engine must do the same. For example, if the fire station islocated at (30, 40) and a fire occurs at town 4, the fire engine has to travel *80 2 30* 1 * 60 2 40* 5 70 miles to the fire.
a. Determine where the fire station should be located.b. Use SolverTable to see how the optimal location of the fire station changes as the number of fires at town 3 changes.
Monroe County is trying to determine where to place the county fire station. The locations of the county’s four major towns are as follows: (10, 20), (60, 20), (40, 30), and (80, 60) (see Figure 7.50). Town 1 averages 40 fires per year; town 2, 25 fires; town 3, 20 fires; and town 4, 30 fires. The county wants to build the fire station in a location that minimizes the average distance that a fire engine must travel to respond to a fire. Because most roads run in either an east-west or a north-south direction, the fire engine must do the same. For example, if the fire station is located at (30, 40) and a fire occurs at town 4, the fire engine has to travel |80 - 30| + |60 - 40| = 70 miles to the fire.
a. Determine where the fire station should be located. Round your answers to three decimal places.
X
Y
Location of fire station
Dr. Barton hypothesizes that if 1st grade students are assigned to practice sight word flashcards for 10 minutes every day for their first semester, they will end up reading more books in their second semester. She creates two groups of 25 students each and gives each group the same sight word flashcards. Group A is assigned to practice with the flashcards for 10 minutes every day for their first semester. Group B is not given this assignment. Each group is tasked with keeping a reading log during their second semester. At the end of 1st grade, Dr. Barton counts how many books each group has read. Group A read 68 books, and Group B read 92 books.
The control group is:
The independent variable is:
The dependent variable is:
This study shows that there is a positive correlation between 10 minutes of daily flashcard practice of sight words and the amount of books read. T/F
This study is an example of descriptive research. T/F
Chapter 10 Solutions
Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
Ch. 10.1 - Fill in the missing entries in the stochastic...Ch. 10.1 - Prob. 2PPCh. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - In Exercises 1 and 2, determine whether P is a...Ch. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - In Exercises 5 and 6, the transition matrix P for...Ch. 10.1 - Prob. 6ECh. 10.1 - In Exercises 7 and 8, the transition matrix P for...Ch. 10.1 - In Exercises 7 and 8, the transition matrix P for...
Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider a pair of Ehrenfest urns labeled A and B....Ch. 10.1 - Consider an unbiased random walk on the set...Ch. 10.1 - Consider a biased random walk on the set {1,2,3,4}...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 13 and 14, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - In Exercises 15 and 16, find the transition matrix...Ch. 10.1 - The mouse is placed in room 2 of the maze shown...Ch. 10.1 - The mouse is placed in room 3 of the maze shown...Ch. 10.1 - Prob. 19ECh. 10.1 - In Exercises 19 and 20, suppose a mouse wanders...Ch. 10.1 - Prob. 21ECh. 10.1 - In Exercises 21 and 22, mark each statement True...Ch. 10.1 - The weather in Charlotte, North Carolina, can be...Ch. 10.1 - Suppose that whether it rains in Charlotte...Ch. 10.1 - Prob. 25ECh. 10.1 - Consider a set of five webpages hyperlinked by the...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Consider a model for signal transmission in which...Ch. 10.1 - Prob. 29ECh. 10.1 - Another model for diffusion is called the...Ch. 10.1 - To win a game in tennis, one player must score...Ch. 10.1 - Volleyball uses two different scoring systems in...Ch. 10.1 - Prob. 33ECh. 10.2 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.2 - In Exercises 1 and 2, consider a Markov chain on...Ch. 10.2 - Prob. 2ECh. 10.2 - In Exercises 3 and 4, consider a Markov chain on...Ch. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - In Exercises 5 and 6, find the matrix to which Pn...Ch. 10.2 - In Exercises 7 and 8, determine whether the given...Ch. 10.2 - Prob. 8ECh. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider a pair of Ehrenfest urns with a total of...Ch. 10.2 - Consider an unbiased random walk with reflecting...Ch. 10.2 - Consider a biased random walk with reflecting...Ch. 10.2 - Prob. 13ECh. 10.2 - In Exercises 13 and 14, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - In Exercises 15 and 16, consider a simple random...Ch. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Consider the mouse in the following maze, which...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - In Exercises 21 and 22, mark each statement True...Ch. 10.2 - Prob. 23ECh. 10.2 - Suppose that the weather in Charlotte is modeled...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - In Exercises 25 and 26, consider a set of webpages...Ch. 10.2 - Prob. 27ECh. 10.2 - Consider beginning with an individual of known...Ch. 10.2 - Prob. 29ECh. 10.2 - Consider the Bernoulli-Laplace diffusion model...Ch. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Let 0 p, q 1, and define P = [p1q1pq] a. Show...Ch. 10.2 - Let 0 p, q 1, and define P = [pq1pqq1pqp1pqpq]...Ch. 10.2 - Let A be an m m stochastic matrix, let x be in m...Ch. 10.2 - Prob. 37ECh. 10.2 - Consider a simple random walk on a finite...Ch. 10.2 - Prob. 39ECh. 10.3 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.3 - Prob. 1ECh. 10.3 - In Exercises 16, consider a Markov chain with...Ch. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Consider an unbiased random walk with absorbing...Ch. 10.3 - In Exercises 13 and 14, consider a simple random...Ch. 10.3 - Prob. 14ECh. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - In Exercises 15 and 16, consider a simple random...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Consider the mouse in the following maze from...Ch. 10.3 - Prob. 19ECh. 10.3 - In Exercises 19 and 20, consider the mouse in the...Ch. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Suppose that the weather in Charlotte is modeled...Ch. 10.3 - Prob. 24ECh. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - The following set of webpages hyperlinked by the...Ch. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - In Exercises 33 and 34, consider the Markov chain...Ch. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.4 - Consider the Markov chain on {1, 2, 3, 4} with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 1-6, consider a Markov chain with...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10, consider a simple random walk...Ch. 10.4 - In Exercises 7-10: consider a simple random walk...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Reorder the states in the Markov chain in Exercise...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Find the transition matrix for the Markov chain in...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - Consider the mouse in the following maze from...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - In Exercises 21-22, mark each statement True or...Ch. 10.4 - Confirm Theorem 5 for the Markov chain in Exercise...Ch. 10.4 - Prob. 24ECh. 10.4 - Consider the Markov chain on {1, 2, 3} with...Ch. 10.4 - Follow the plan of Exercise 25 to confirm Theorem...Ch. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.5 - Prob. 1PPCh. 10.5 - Consider a Markov chain on {1, 2, 3, 4} with...Ch. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - In Exercises 13, find the fundamental matrix of...Ch. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Consider a simple random walk on the following...Ch. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Consider the mouse in the following maze from...Ch. 10.5 - In Exercises 21 and 22, mark each statement True...Ch. 10.5 - Prob. 22ECh. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Suppose that the weather in Charlotte is modeled...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Consider a set of webpages hyperlinked by the...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 27-30 concern the Markov chain model for...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Exercises 31-36 concern the two Markov chain...Ch. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Consider a Markov chain on {1, 2, 3, 4, 5, 6} with...Ch. 10.5 - Consider a Markov chain on {1,2,3,4,5,6} with...Ch. 10.5 - Prob. 39ECh. 10.6 - Let A be the matrix just before Example 1. Explain...Ch. 10.6 - Prob. 2PPCh. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Major League batting statistics for the 2006...Ch. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - In the previous exercise, let p be the probability...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- What operations can be performed on a linear system to arrive at an equivalent system?arrow_forwardIn Flatland there are four cities, Abbott, Banchoff, Charlie and Dimension. The distance from The distance from Abbott to Banchoff is 9 miles. The distance from Abbott to Charlie is 8 miles. The distance from Abbott to Dimension is 11 miles. The distance from Banchoff to Charlie is 15 miles. The distance from Banchoff to Dimension is 13 miles. The distance from Charlie to Dimension is 12 miles. Sketch a graph to represent the traveling salesman problem for this situation, and find the length of the shortest path. Remember to begin and end in the same city. The shortest path is miles.arrow_forwardThere are two alternative Plans for operating a high-speed inter-city rail service. In Plan I, the service connects city A with city B through city C where the rail makes a stop to load or unload passengers. The rail transportation system is assumed to be perfectly symmetrical with respect to direction of travel. PLAN I The link travel times are 2 hours between each pair of cities in both directions. The time it takes to service the train at each node is 0.5 hours. In the alternative Plan II, the train company considers to stop servicing the smaller city C, in order to provide a better level of service for the users in the city A and city B. PLAN II According to Plan II, the travel time between the major cities A and B in both directions will be reduced to 3.5 hours. The time it takes to service the train in both city A and city B is still 0.5 hours. Q2 (A) Calculate the train-cycle for Plan I and Plan II. Q2 (B) How many trains do you need to operate 12 trains/day uniformly…arrow_forward
- Consider the following rooms from a hotel: D2 Room 217 Room 218 D1 D3 Hallway D6 D4 Room 318 Room 317 D5 A. Please draw a graph that shows how the various rooms are connected to each-other by doorways (count the Hallway as a normal room) B. Please give a walk from room 217 to room 318 that is not a trail. c. Is there an Euler circuit through these rooms? 1.e., is it possible to walk around the rooms, starting and ending in the same room, and visiting every room while passing through each door exactly once? Please give such a circuit, if one exists, or say how you know that no such circuit exists.arrow_forwardI don't know how to accurately answer this question. I have followed the steps and have gotten 3 different answers each time. I am not sure which step I am missing or messing up on. I don't know if I am using the wrong formula but I would appreciate as much help as possible by guiding me through each step. Thank you so much.arrow_forwardshow solutionarrow_forward
- A tortoise and hare are competing in a 400-meter race. The arrogant hare gives the tortoise a 220-meter head start. When the start gun is fired, the hare begins running at a constant speed of 3.5 meters per second and the tortoise begins crawling at constant speed of 1.5 meters per second. Take out a piece of paper and read the above problem context again. You will prepare your written work and solutions on your own paper and upload it and the end of this question. Complete the problem solving process by: i. reading and re-reading the problem to identify the quantities in the situation; ii. making a drawing to represent the relevant quantities in the situation; iii. and defining the variable t to represent the number of seconds since the start of the race. a. Define a function f to determine the distance of the tortoise from the finish line in terms of the number of seconds, t, since the start of the race. Preview Solve f(t) = 0 and describe what your solution represents. t = Preview…arrow_forwardConsider the illustration below. [If you have any trouble viewing this illustration, please let me know; note that it is also available in the textbook problems for 3.7 as specified.] Suppose that a group of robots is traversing this maze. At each step, each robot will choose a path and move along it, where it is equally likely to select each available path and cannot choose to stay where it is. (At the end of each step, each robot will be in one of the four numbered rooms.) Part (a): Construct the appropriate transition matrix for the Markov chain modeling this scenario. Part (b): Find the steady state probability vector.arrow_forwardsuppose Gabe , an elementary school student , has just finished dinner with his mother , judy. Eyeing the nearby cookie jar, Gabe asks his mother if he can have cookie foe dessert. She tells Gabe that she needs to check his backpack to make sure that he finished his homework. Gabe cannot remember where he left his backpack, but he knows for sure that he did not complete his homework and will not be allowed to eat a cookie. Gabe believes his only option is to quickly steal a cookie while his mother is out of the room. Judy then leaves the room to look for Gabes backpack. Assume that judy could return at any time in the next 60 seconds with equal probability . For the first 20 seconds, Gabe sheepishly wonders if he will get caught trying to grab a nearby cookie. After waiting and not seeing his mother , Gabe decides that he needs a cookie and begins to take one from the jar. Assuming it takes Gabe 30 seconds to grab a cookie from the jar and devour it without a trace, what is the…arrow_forward
- USA. Benjamin Banneker (1731-1806) is one of the great American heroes of all time. The son and grandson of Africans captured and enslaved, he was fortunate to have been born free. He inherited the family farm where he worked hard all of his life. As a child he had a few months of schooling. Everything else he had to do on his own. He loved mathematics and science but did not get a chance to learn astronomy until he was in his fifties. Then he performed a near miracle, learning it all in less than a year. In his hand-written journal, he recorded two right triangle examples that interested him. You can solve them here and remember the great man who enjoyed geometry. On the page in his journal next to the August 1775 astronomy calculations, Banneker wrote, in the style of that time: Suppose a ladder 60 feet long be placed in a Street so as to reach a window on the one Side 37 feet high, and without moving it at bottom, will reach another window on the other side of teh Street which is 23…arrow_forwardThe Phony TV company makes two different types of television sets, OLED and LED, which are assembled by two different assembly lines. When Line One operates it assembles 30 units of the OLED model and 50 units of the LED model per hour. Line Two assembles 40 units of the OLED model and 40 units of the LED model per hour. Let x be the number of hours that Line One operates and y the number of hours Line Two operates. Phony needs to produce at least 3000 units of the OLED model and 4000 units of the LED model to fill an order. (a) Write down the inequalities that describe the assembly constraints. (b) Graph the feasible region determined by these constraints.arrow_forwardTask C has two immediate predecessors, tasks A and B. Task A has an early finish time of 3 days, and task B has an early finish time of 5 days. Task C is 2 days long. What is the early finish time of task C?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Minimum cuts and maximum flow rate; Author: Juddy Productions;https://www.youtube.com/watch?v=ylxhl1ipWss;License: Standard YouTube License, CC-BY