Fundamentals of Physics Extended
10th Edition
ISBN: 9781118230725
Author: David Halliday, Robert Resnick, Jearl Walker
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10, Problem 67P
GO Figure 10-48 shows a rigid assembly of a thin hoop (of mass m and radius R = 0.150 m) and a thin radial rod (of mass m and length L = 2.00R). The assembly is upright, hut If we give it a slight nudge, it will rotate around a zontal axis in the plane of the rod. Assuming that the energy given to the assembly in such a nudge is negligible, what would be the assembly's angular speed about the rotation axis when it passes through the upside-down (inverted) orientation?
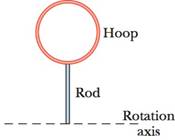
Figure 10-48 Problem 67
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The determined Wile E. Coyote is out once more to try to capture the elusive Road Runner of Loony Tunes fame. The coyote is strapped to a rocket, which provide a constant horizontal acceleration of 15.0 m/s2. The coyote starts off at rest 79.2 m from the edge of a cliff at the instant the roadrunner zips by in the direction of the cliff. If the roadrunner moves with constant speed, find the minimum velocity the roadrunner must have to reach the cliff before the coyote. (proper sig fig)
Hello, I need some help with calculations for a lab, it is Kinematics: Finding Acceleration Due to Gravity. Equations: s=s0+v0t+1/2at2 and a=gsinθ. The hypotenuse,r, is 100cm (given) and a height, y, is 3.5 cm (given). How do I find the Angle θ1? And, for distance traveled, s, would all be 100cm? For my first observations I recorded four trials in seconds: 1 - 2.13s, 2 - 2.60s, 3 - 2.08s, & 4 - 1.95s. This would all go in the coloumn for time right? How do I solve for the experimental approximation of the acceleration? Help with trial 1 would be great so I can use that as a model for the other trials. Thanks!
After the countdown at the beginning of a Mario Kart race, Bowser slams on the gas, taking off from rest. Bowser get up to a full speed of 25.5 m/s due to an acceleration of 10.4 m/s2. A)How much time does it take to reach full speed? B) How far does Bowser travel while accelerating?
Chapter 10 Solutions
Fundamentals of Physics Extended
Ch. 10 - Figure 10-20 is a graph of the angular velocity...Ch. 10 - Figure 10-21 shows plots of angular position ...Ch. 10 - A force is applied to the rim of a disk that can...Ch. 10 - Figure 10-22b is a graph of the angular position...Ch. 10 - In Fig. 10-23, two forces F1 and F2 act on a disk...Ch. 10 - In the overhead view of Fig. 10-24, five forces of...Ch. 10 - Figure 10-25a is an overhead view of a horizontal...Ch. 10 - Figure l0-25b shows an overhead view of a...Ch. 10 - Figure 10-26 shows a uniform metal plate that had...Ch. 10 - Figure 10-27 shows three flat disks of the same...
Ch. 10 - Figure 10-28a shows a meter stick, hall wood and...Ch. 10 - Figure 10-29 shows three disks, each with a...Ch. 10 - A good baseball pitcher can throw a baseball...Ch. 10 - What is the angular speed of a the second hand, b...Ch. 10 - When a slice of buttered toast is accidentally...Ch. 10 - The angular position of a point on a rotating...Ch. 10 - ILW A diver makes 2.5 revolutions on the way from...Ch. 10 - The angular position of a point on the rim of a...Ch. 10 - The wheel in Fig. 10-30 has eight equally spaced...Ch. 10 - The angular acceleration of a wheel is = 6.0t4 ...Ch. 10 - A drum rotates around its central axis at an...Ch. 10 - Starting from rest, a disk rotates about its...Ch. 10 - A disk, initially rotating at 120 rad/s, is slowed...Ch. 10 - The angular speed of an automobile engine is...Ch. 10 - ILW A flywheel turns through 40 rev as it slows...Ch. 10 - GO A disk rotates about its central axis starling...Ch. 10 - SSM Starting from rest, a wheel has constant =...Ch. 10 - A merry-go-round rotates from rest with an angular...Ch. 10 - At t = 0, a flywheel has an angular velocity of...Ch. 10 - A pulsar is a rapidly rotating neutron star that...Ch. 10 - What are the magnitudes of a the angular velocity,...Ch. 10 - An object rotates about a fixed axis, and the...Ch. 10 - Between 1911 and 1990, the top of the leaning bell...Ch. 10 - An astronaut is tested in a centrifuge with radius...Ch. 10 - SSM WWW A flywheel with a diameter of 1.20 m is...Ch. 10 - A vinyl record is played by rotating the record so...Ch. 10 - SSM a What is the angular speed about the polar...Ch. 10 - The flywheel of a steam engine runs with a...Ch. 10 - A seed is on a turntable rotating at 3313 rev/min,...Ch. 10 - In Fig. 10-31, wheel A of radius rA = 10 cm is...Ch. 10 - Figure 10-32 shows an early method of measuring...Ch. 10 - A gyroscope flywheel of radius 2.83 cm is...Ch. 10 - GO A disk, with a radius of 0.25 m. is to be...Ch. 10 - A car starts from rest and moves around a circular...Ch. 10 - SSM Calculate the rotational inertia of a wheel...Ch. 10 - Figure 10-33 gives angular speed versus time for a...Ch. 10 - SSM Two uniform solid cylinders, each rotating...Ch. 10 - Figure 10-34a shows a disk that can rotate about...Ch. 10 - SSM Calculate the rotational inertia of a meter...Ch. 10 - Figure 10-35 shows three 0.0100 kg particles that...Ch. 10 - Trucks can be run on energy stored in a rotating...Ch. 10 - Figure 10-36 shows an arrangement of 15 identical...Ch. 10 - GO In Fig. 10-37, two particles, each with mass m...Ch. 10 - The masses and coordinates of four particles are...Ch. 10 - SSM WWW The uniform solid block in Fig. 10-38 has...Ch. 10 - Four identical particles of mass 0.50 kg each are...Ch. 10 - SSM ILW The body in Fig. 10-39 is pivoted at O,...Ch. 10 - The body in Fig. 10-40 is pivoted at O. Three...Ch. 10 - SSM A small ball of mass 0.75 kg is attached to...Ch. 10 - The length of a bicycle pedal arm is 0.152 m, and...Ch. 10 - SSM ILW During the launch from a board, a divers...Ch. 10 - If a 32.0 N m torque on a wheel causes angular...Ch. 10 - Prob. 51PCh. 10 - GO In Fig. 10-42, a cylinder having a mass of 2.0...Ch. 10 - GO Figure 10-43 shows a uniform disk that can...Ch. 10 - In a judo foot-sweep move, you sweep your...Ch. 10 - In Fig. 10-45a, an irregularly shaped plastic...Ch. 10 - Figure 10-46 shows particles 1 and 2, each of mass...Ch. 10 - GO A pulley, with a rotational inertia of 1.0 103...Ch. 10 - a IF R= 12 cm, M = 400 g, and m = 50 g in Fig....Ch. 10 - An automobile crankshaft transfers energy from the...Ch. 10 - A thin rod of length 0.75 m and mass 0.42 kg is...Ch. 10 - A 32.0 kg wheel, essentially a thin hoop with...Ch. 10 - In Fig. 10-35, three 0.0100 kg particles have been...Ch. 10 - SSM ILW A meter stick is held vertically with one...Ch. 10 - A uniform cylinder of radius 10 cm and mass 20 kg...Ch. 10 - GO A tall, cylindrical chimney fall;; over when...Ch. 10 - GO A uniform spherical shell of mass M = 4.5 kg...Ch. 10 - GO Figure 10-48 shows a rigid assembly of a thin...Ch. 10 - Prob. 68PCh. 10 - Prob. 69PCh. 10 - A wheel, starling from rest, rotates with a...Ch. 10 - SSM In Fig. 10-50, two 6.20 kg blocks are...Ch. 10 - Prob. 72PCh. 10 - A uniform helicopter rotor blade is 7.80 m long,...Ch. 10 - Prob. 74PCh. 10 - Prob. 75PCh. 10 - Starting from rest at t = 0, a wheel undergoes a...Ch. 10 - SSM A record turntable rotating at 3313 rev/min...Ch. 10 - Prob. 78PCh. 10 - Prob. 79PCh. 10 - A disk rotates al constant angular acceleration,...Ch. 10 - GO The thin uniform rod in Fig. 10-53 has length...Ch. 10 - Prob. 82PCh. 10 - Prob. 83PCh. 10 - At 7:14 A.M. on June 30, 1908, a huge explosion...Ch. 10 - A golf ball is launched at an angle of 20 to the...Ch. 10 - Prob. 86PCh. 10 - GO IN Fig. 10-55, a wheel of radius 0.20 m is...Ch. 10 - A thin spherical shell has a radius of 1.90 m. An...Ch. 10 - Prob. 89PCh. 10 - The flywheel of an engine is rotating at 25.0...Ch. 10 - SSM In Fig. 10-19a, a wheel of radius 0.20 m is...Ch. 10 - Our Sun is 23 104 ly light-years from the center...Ch. 10 - SSM A wheel of radius 0.20 m is mounted on a...Ch. 10 - If an airplane propeller rotates at 2000 rev/min...Ch. 10 - The rigid body shown in Fig. 10-57 consists of...Ch. 10 - Beverage engineering. The pull tab was a major...Ch. 10 - Figure 10-58 shows a propeller blade that rotates...Ch. 10 - A yo-yo-shaped device mounted on a horizontal...Ch. 10 - Prob. 99PCh. 10 - Two thin rods each of mass 0.20 kg are joined...Ch. 10 - In Fig. 10-61, four pulleys are connected by two...Ch. 10 - Prob. 102PCh. 10 - In Fig. 10-63, a thin uniform rod mass 3.0 kg,...Ch. 10 - Prob. 104PCh. 10 - Prob. 105PCh. 10 - A point on the rim of a 0.75-m-diameler grinding...Ch. 10 - A pulley wheel that is 8.0 cm in diameter has a...Ch. 10 - A vinyl record on a turntable rotates at 3313...
Additional Science Textbook Solutions
Find more solutions based on key concepts
All of the following processes are involved in the carbon cycle except: a. photosynthesis b. cell respiration c...
Human Biology: Concepts and Current Issues (8th Edition)
3. Which of the following is a major functional characteristic of all organisms? (a) movement, (b) growth (c) m...
Human Anatomy & Physiology (Marieb, Human Anatomy & Physiology) Standalone Book
5. In a type of parakeet known as a “budgie,” feather color is controlled by two genes. A yellow pigment is syn...
Genetic Analysis: An Integrated Approach (3rd Edition)
Answer the following questions for each compound: a. How many signals are in its 13C NMR spectrum? b. Which sig...
Organic Chemistry (8th Edition)
Choose the best answer to each of the following. Explain your reasoning. What is the leading hypothesis for Ven...
Cosmic Perspective Fundamentals
Match the following cell types with their correct definition. _________Macrophage _________NK cell _________Eos...
Human Anatomy & Physiology (2nd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Side 1 has an area of 1.90 m^2, Side 2 has an area of 3.90 m^2, the electric field in magnitude is around 215 N/C. Please find the electric flux magnitude through side 1 and 2 combined if the angle (theta) made between the electric field with side 2 is 30.0 degrees. I believe side 1 is 60 degrees but could be wrong. Thank you.arrow_forwardAfter the countdown at the beginning of a Mario Kart race, Bowser slams on the gas, taking off from rest. Bowser get up to a full speed of 25.5 m/s due to an acceleration of 10.4 m/s2.arrow_forwardThe drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Side 1 has an area of 1.90 m^2, Side 2 has an area of 3.90 m^2, the electric field in magnitude is around 215 N/C. Please find the electric flux magnitude through side 1 and 2 combined if the angle (theta) made between the electric field with side 2 is 30.0 degrees. Thank you.arrow_forward
- The drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Surface (1) has an area of 1.90 m^2, while Surface (2) has an area of 3.90 m^2. The electric field in magnitude of 215 N/C. Please find the magnitude of the electric flux through surface (with both 1 and 2 combined) if the angle (theta) made between the electric field with surface (2) is 30.0 degrees. Thank you.arrow_forwardThe drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Surface (1) has an area of 1.90 m^2, while Surface (2) has an area of 3.90 m^2. The electric field in magnitude of 215 N/C. Please find the magnitude of the electric flux through surface (with both 1 and 2 combined) if the angle (theta) made between the electric field with surface (2) is 30.0 degrees. Thank you.arrow_forwardAccording to a grade 11 Physics SPH3U course Kinematics, Dynamics, and Energy answer the following questionarrow_forward
- According to a grade 11 Physics SPH3U course Kinematics, Dynamics, and Energy answer the following questionarrow_forwardAccording to a grade 11 Physics SPH3U course Kinematics, Dynamics, and Energy answer the following questionarrow_forwardThree point-like charges in the attached image are placed at the corners of an equilateral triangle as shown in the figure. Each side of the triangle has a length of 38.0 cm, and the point (C) is located half way between q1 and q3 along the side. Find the magnitude of the electric field at point (C). Let q1 = −2.80 µC, q2 = −3.40 µC, and q3 = −4.50 µC. Thank you.arrow_forward
- Three point-like charges are placed as shown in the attach image, where r1 = r2 = 44.0 cm. Find the magnitude of the electric force exerted on the charge q3. Let q1 = -1.90 uC, q2 = -2.60 uC, and q3 = +3.60 uC. Thank you.arrow_forwardThe drawing attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Surface (1) has an area of 1.90 m², while Surface (2) has an area of 3.90 m². The electric field in magnitude of 215 N/C. Find the magnitude of the electric flux through surface (1 and 2 combined) if the angle theta made between the electric field with surface (2) is 30.0 degrees. Thank you.arrow_forwardA car driving at 27m/s veers to the left to avoid a deer in the road. The maneuver takes 2.0s and the direction of travel is altered by 20 degrees. What is the average acceleration during the constant speed maneuver? Do this in accordance with the example in the chapter.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
28.1 Rigid Bodies; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=u_LAfG5uIpY;License: Standard YouTube License, CC-BY