Mechanics of Materials (MindTap Course List)
9th Edition
ISBN: 9781337093347
Author: Barry J. Goodno, James M. Gere
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10, Problem 10.4.17P
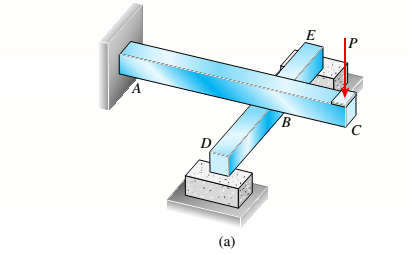
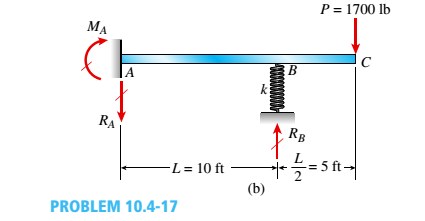
Beam ABC is fixed at support A and rests (at point B) upon the midpoint of beam DE (see part a of the figure). Thus, beam, ABC may be represented as a propped cantilever beam with an overhang BC and a linearly elastic support of stiffness k at point B (see part b of the figure).
The distance from A to B is L = 10 ft, the distance from B to C is L/2 = 5 ft, and the length of beam DE is L = 10 ft. Both beams have the same flexural rigidity EI. A concentrated load P = 1700 lb acts at t lie free end of beam ABC.
Determine the reactions RA, RB+ and MAfor beam ABC. Also, draw the shear-force and bending-moment diagrams for beam ABC, labeling all critical ordinates.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
What are some ways Historical Data can be used and applied to an estimate?
Problem 1. Rod OAB is rotating counterclockwise with the constant angular velocity of 5 rad/s.
In the position shown, collar P is sliding toward A with the constant speed of 0.8 m/s relative to
the rod. Find the velocity of P and the acceleration of P.
y
B
3
P
300 mm
A
-
Answer: Up = -0.861 − 0.48ĵ™; ā₂ = 4.8î −1.1ĵ
m
A bent tube is attached to a wall with brackets as shown. . A
force of F = 980 lb is applied to the end of the tube with
direction indicated by the dimensions in the figure.
a.) Determine the force vector F in Cartesian components.
→
→
b.) Resolve the force vector F into vector components
parallel and perpendicular to the position vector rDA.
Express each of these vectors in Cartesian components.
2013 Michael Swanbom
cc 10
BY NC SA
g
x
B
A
א
Z
FK
с
кая
b
Values for dimensions on the figure are given in the table
below. Note the figure may not be to scale. Be sure to align
your cartesian unit vectors with the coordinate axes shown in
the figure.
Variable
Value
a
8 in
12 in
с
15 in
36 in
h
23 in
g
28 in
a. F =
b. FDA =
= (
+
k) lb
k) lb
FIDA =
2 +
k) lb
Chapter 10 Solutions
Mechanics of Materials (MindTap Course List)
Ch. 10 - A propped cantilever steel beam is constructed...Ch. 10 - A fixed-end b earn is subjected to a point load at...Ch. 10 - A propped cantilever beam AB of a length L is...Ch. 10 - A fixed-end beam AB of a length L supports a...Ch. 10 - A cantilever beam AB of a length L has a fixed...Ch. 10 - A cantilever beam of a length L and loaded by a...Ch. 10 - A cantilever beam has a length L and is loaded by...Ch. 10 - A propped cantilever beam of a length L is loaded...Ch. 10 - A propped cantilever beam of a length L is loaded...Ch. 10 - A fixed-end beam of a length L is loaded by a...
Ch. 10 - A fixed-end b earn of a length L is loaded by a...Ch. 10 - A fixed-end beam of a length L is loaded by...Ch. 10 - A counterclockwise moment M0acts at the midpoint...Ch. 10 - A propped cantilever beam of a length L is loaded...Ch. 10 - A propped cantilever beam is subjected to uniform...Ch. 10 - Repeat Problem 10.3-15 using L = 3.5 m, max = 3...Ch. 10 - A two-span, continuous wood girder (E = 1700 ksi)...Ch. 10 - A fixed-end beam AB carries point load P acting at...Ch. 10 - A fixed-end beam AB supports a uniform load of...Ch. 10 - -4-4 A cantilever beam is supported at B by cable...Ch. 10 - A propped cantilever beam AB of a length L carries...Ch. 10 - A beam with a sliding support at B is loaded by a...Ch. 10 - A propped cantilever beam of a length 2L with a...Ch. 10 - The continuous frame ABC has a pin support at /l,...Ch. 10 - The continuous frame ABC has a pin support at A,...Ch. 10 - Beam AB has a pin support at A and a roller...Ch. 10 - The continuous frame ABCD has a pin support at B:...Ch. 10 - Two flat beams AB and CD, lying in horizontal...Ch. 10 - -4-13 A propped cantilever beam of a length 2L is...Ch. 10 - A propped cantilever beam of a length 2L is loaded...Ch. 10 - Determine the fixed-end moments (MAand MB) and...Ch. 10 - A continuous beam ABC wit h two unequal spans, one...Ch. 10 - Beam ABC is fixed at support A and rests (at point...Ch. 10 - A propped cantilever beam has flexural rigidity EI...Ch. 10 - A triangularly distributed 1oad with a maximum...Ch. 10 - A fixed-end beam is loaded by a uniform load q =...Ch. 10 - Uniform load q = 10 lb/ft acts over part of the...Ch. 10 - A propped cantilever beam with a length L = 4 m is...Ch. 10 - A cant i levé r b ea m i s supported by a tie rod...Ch. 10 - The figure shows a nonprismatic, propped...Ch. 10 - A beam ABC is fixed at end A and supported by beam...Ch. 10 - A three-span continuous beam A BCD with three...Ch. 10 - A beam rests on supports at A and B and is loaded...Ch. 10 - A propped cantilever beam is subjected to two...Ch. 10 - A propped cantilever beam is loaded by a...Ch. 10 - A fixed-end beam AB of a length L is subjected to...Ch. 10 - A temporary wood flume serving as a channel for...Ch. 10 - Two identical, simply supported beams AB and CD...Ch. 10 - The cantilever beam AB shown in the figure is an...Ch. 10 - The beam AB shown in the figure is simply...Ch. 10 - The continuous frame ABC has a fixed support at A,...Ch. 10 - The continuous frame ABC has a pinned support at...Ch. 10 - A wide-flange beam ABC rests on three identical...Ch. 10 - A fixed-end beam AB of a length L is subjected to...Ch. 10 - A beam supporting a uniform load of intensity q...Ch. 10 - A thin steel beam AB used in conjunction with an...Ch. 10 - Find an expression for required moment MA(in terms...Ch. 10 - Repeat Problem 10.4-41 for the loading shown in...Ch. 10 - A propped cantilever beam is loaded by two...Ch. 10 - A cable CD of a length H is attached to the third...Ch. 10 - A propped cantilever beam, fixed at the left-hand...Ch. 10 - Solve t he preceding problem by integrating the...Ch. 10 - A two-span beam with spans of lengths L and L/3 is...Ch. 10 - Solve the preceding problem by integrating the...Ch. 10 - Assume that the deflected shape of a beam AB with...Ch. 10 - (a) A simple beam AB with length L and height h...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Problem 4. Part 1 100 mm C @ PROBLEM 15.160 Pin P slides in the circular slot cut in the plate shown at a constant relative speed u = 500 mm/s. Assuming that at the instant shown the angular velocity of the plate is 6 rad/s and is increasing at the rate of 20 rad/s², determine the acceleration of pin P when = 90°. 150 mm is NOT zero. Answer: a = 3.4î −15.1ĵ m/s² ) P (Hint: u is a constant number, which means that the tangential component of F is zero. However, the normal component of Part2. When 0 = 120°, u = 600 mm/s and is increasing at the rate of 30mm/s², determine the acceleration of pin P.arrow_forwardProblem 5. Disk D of the Geneva mechanism rotates with constant counterclockwise angular velocity wD = 10 rad/s. At the instant when & = 150º, determine (a) the angular velocity of disk S, and (b) the velocity of pin P relative to disk S. (c). the angular acceleration of S. Disk S R=50 mm =135° |1=√ER- Disk D Partial answers: Ō = -4.08 Â rad/s ā¸ = -233 k rad/s²arrow_forwardProblem 3. In the figure below, point A protrudes from link AB and slides in the rod OC. Rod OC is rotating with angular velocity woc = 2 rad/s and aoc = 3 rad/s² in the directions shown. Find the following, remembering to clearly define your axes and the rate of rotation of the frame. a. The angular velocity of link AB and the velocity of A relative to rod OC. m (Answers: @AB is 2.9 rad/s CCW, rxy = .58! toward C) S b. The angular acceleration of link AB and the acceleration of A relative to rod OC. Answers: αAB = 7.12 rad/s² CCW, r = 6.3 m ܐܨ toward C. B C A 30° Фос 400 mm OA=500 mm docarrow_forward
- Problem 2. 6 m 30° B PROBLEM 15.164 At the instant shown the length of the boom AB is being decreased at the constant rate of 0.2 m/s and the boom is being lowered at the constant rate of 0.08 rad/s. Determine (a) the velocity of Point B, (b) the acceleration of Point B. Partial answer: a = −0.049î +0.009ĵ m/s²arrow_forwardA crate is hung by three ropes attached to a steel ring at A such that the top surface is parallel to the xy plane. Point A is located at a height of h = 121.92 cm above the top of the crate directly over the geometric center of the top surface. Use the given dimensions from the table below to perform the following calculations: →> a.) Determine the position vector IAD that describes rope AD. b.) Compute the unit vector cд that points from point C to point A. c.) If rope AB carries a tension force of magnitude FT = 760 → N, determine the force vector FT that expresses how this force acts on point A. Express each vector in Cartesian components to three significant figures. 2013 Michael Swanbom ↑z BY NC SA b x B У a D Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Be sure to align your cartesian unit vectors with the coordinate axes shown in the figure. Variable Value a 101.6 cm b 124.46 cm с 38.71 cm a. rдD = + b. ÛCA c. FT= =…arrow_forwardF3 N< Ꮎ 2 F2 -Y F1 There are 3 forces acting on the eye bolt. Force F1 acts on the XY plane has a magnitude of 536 lbf, and the angle of 0 = 38°. Force F2 acts on the YZ plane has a magnitude of 651 lbf, and the angle = 41°. Force F3 has a magnitude of 256 lb, and coordinate. = f direction angles of a 71°, B = 115°, and y = 33°. Determine the resultant force on the eye bolt. FR = ( + k) lbf FR magnitude: FR coordinate direction angle a: deg FR coordinate direction angle ẞ`: deg FR coordinate direction angle y: deg lbfarrow_forward
- Ball joints connect the ends of each of the struts as shown. The resulting structure supports a force of F = 1925 N which lies in the xz plane. a.) Determine the angle (in degrees) between strut AD and strut AC. b.) Determine the dimension g such that the force Fis →> perpendicular to гAC. 2013 Michael Swanbom CC BY NC SA B b C h/ L 不 g F ୮ d y LLC Values for dimensions on the figure are given in the table below. Note the figure may not be to scale. Be sure to align your cartesian unit vectors with the coordinate axes shown in the figure. Variable Value a 4.8 cm b 13.4 cm C 11.6 cm d 10.4 cm h 4.4 cm k 14.8 cm a. The angle between strut AD and strut AC is b. The dimension g is deg. cm.arrow_forward13 F1 35 N = 37°. = Determine the resultant force on the eye bolt. FR = ( + FR magnitude: FR coordinate direction angle a: deg FR coordinate direction angle ẞ`: Ꭱ deg FR coordinate direction angle y: deg N k) Narrow_forwardA hollow cylinder with inner radius of 30 mm and outer radius of 50 mm is heated at the inner surface at a rate of 10^5m^2W and dissipated heat by convection from outer surface into a fluid at 80∘C with h=400 m2 KW. There is no energy generation and thermal conductivity of the material is constant at 15mKW. Calculate the temperature of inside and outside surfaces of cylinder.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Mechanics of Materials Lecture: Beam Design; Author: UWMC Engineering;https://www.youtube.com/watch?v=-wVs5pvQPm4;License: Standard Youtube License