Mechanics of Materials (MindTap Course List)
9th Edition
ISBN: 9781337093347
Author: Barry J. Goodno, James M. Gere
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10, Problem 10.3.6P
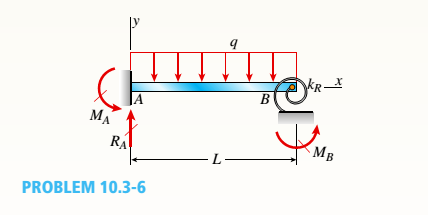
A cantilever beam of a length L and loaded by a uniform load of intensity q has a fixed support at A and spring support at B with rotational stiffness kR. A rotation
Find rotation
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
اه
: +0
العنوان
solle
не
эт
4
كا
- pu+965
A heavy car plunges into a lake during an accident and lands at the bottom of the lake
on its wheels as shown in figure. The door is 1.2 m high and I m wide, and the top edge of
the door is 8 m below the free surface of the water. Determine the hydrostatic force on the
er of the door, and discuss if 10 the masse
door if it is located at the center o
if the driver can open the door, if
Answer the following statements by True or False:
1. Superchargers are used to increase the power of an IC engine by raising the
intake pressure and thus allowing more fuel to be burned per cycle.
2. Scavenging is the process by which the oil rings scrape the lubricating oil
from the cylinder wall and allow the oil to return to the oil pan.
3. The power output of a two-stroke engine equals that of a four-stroke engine
for the same displacement.
4. After coolers are used after the compressor to drop the air temperature and thus
increase its density.
5. The rotary…
Answer the following statements by True or False:
1. Superchargers are used to increase the power of an IC engine by raising the
intake pressure and thus allowing more fuel to be burned per cycle.
2. Scavenging is the process by which the oil rings scrape the lubricating oil
from the cylinder wall and allow the oil to return to the oil pan.
3. The power output of a two-stroke engine equals that of a four-stroke engine
for the same displacement.
4. After coolers are used after the compressor to drop the air temperature and thus
increase its density.
5. The rotary engine has the advantages of better sealing of high pressure gases
and less wear on seals.
16.144 A uniform bar AB, of weight 30 lb and length 3 ft, is attached to the 40-lb cart C. Neglecting friction, determine immediately after the system is released from rest:
a) the acceleration of the cart,b) the angular acceleration of the bar.
Chapter 10 Solutions
Mechanics of Materials (MindTap Course List)
Ch. 10 - A propped cantilever steel beam is constructed...Ch. 10 - A fixed-end b earn is subjected to a point load at...Ch. 10 - A propped cantilever beam AB of a length L is...Ch. 10 - A fixed-end beam AB of a length L supports a...Ch. 10 - A cantilever beam AB of a length L has a fixed...Ch. 10 - A cantilever beam of a length L and loaded by a...Ch. 10 - A cantilever beam has a length L and is loaded by...Ch. 10 - A propped cantilever beam of a length L is loaded...Ch. 10 - A propped cantilever beam of a length L is loaded...Ch. 10 - A fixed-end beam of a length L is loaded by a...
Ch. 10 - A fixed-end b earn of a length L is loaded by a...Ch. 10 - A fixed-end beam of a length L is loaded by...Ch. 10 - A counterclockwise moment M0acts at the midpoint...Ch. 10 - A propped cantilever beam of a length L is loaded...Ch. 10 - A propped cantilever beam is subjected to uniform...Ch. 10 - Repeat Problem 10.3-15 using L = 3.5 m, max = 3...Ch. 10 - A two-span, continuous wood girder (E = 1700 ksi)...Ch. 10 - A fixed-end beam AB carries point load P acting at...Ch. 10 - A fixed-end beam AB supports a uniform load of...Ch. 10 - -4-4 A cantilever beam is supported at B by cable...Ch. 10 - A propped cantilever beam AB of a length L carries...Ch. 10 - A beam with a sliding support at B is loaded by a...Ch. 10 - A propped cantilever beam of a length 2L with a...Ch. 10 - The continuous frame ABC has a pin support at /l,...Ch. 10 - The continuous frame ABC has a pin support at A,...Ch. 10 - Beam AB has a pin support at A and a roller...Ch. 10 - The continuous frame ABCD has a pin support at B:...Ch. 10 - Two flat beams AB and CD, lying in horizontal...Ch. 10 - -4-13 A propped cantilever beam of a length 2L is...Ch. 10 - A propped cantilever beam of a length 2L is loaded...Ch. 10 - Determine the fixed-end moments (MAand MB) and...Ch. 10 - A continuous beam ABC wit h two unequal spans, one...Ch. 10 - Beam ABC is fixed at support A and rests (at point...Ch. 10 - A propped cantilever beam has flexural rigidity EI...Ch. 10 - A triangularly distributed 1oad with a maximum...Ch. 10 - A fixed-end beam is loaded by a uniform load q =...Ch. 10 - Uniform load q = 10 lb/ft acts over part of the...Ch. 10 - A propped cantilever beam with a length L = 4 m is...Ch. 10 - A cant i levé r b ea m i s supported by a tie rod...Ch. 10 - The figure shows a nonprismatic, propped...Ch. 10 - A beam ABC is fixed at end A and supported by beam...Ch. 10 - A three-span continuous beam A BCD with three...Ch. 10 - A beam rests on supports at A and B and is loaded...Ch. 10 - A propped cantilever beam is subjected to two...Ch. 10 - A propped cantilever beam is loaded by a...Ch. 10 - A fixed-end beam AB of a length L is subjected to...Ch. 10 - A temporary wood flume serving as a channel for...Ch. 10 - Two identical, simply supported beams AB and CD...Ch. 10 - The cantilever beam AB shown in the figure is an...Ch. 10 - The beam AB shown in the figure is simply...Ch. 10 - The continuous frame ABC has a fixed support at A,...Ch. 10 - The continuous frame ABC has a pinned support at...Ch. 10 - A wide-flange beam ABC rests on three identical...Ch. 10 - A fixed-end beam AB of a length L is subjected to...Ch. 10 - A beam supporting a uniform load of intensity q...Ch. 10 - A thin steel beam AB used in conjunction with an...Ch. 10 - Find an expression for required moment MA(in terms...Ch. 10 - Repeat Problem 10.4-41 for the loading shown in...Ch. 10 - A propped cantilever beam is loaded by two...Ch. 10 - A cable CD of a length H is attached to the third...Ch. 10 - A propped cantilever beam, fixed at the left-hand...Ch. 10 - Solve t he preceding problem by integrating the...Ch. 10 - A two-span beam with spans of lengths L and L/3 is...Ch. 10 - Solve the preceding problem by integrating the...Ch. 10 - Assume that the deflected shape of a beam AB with...Ch. 10 - (a) A simple beam AB with length L and height h...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- I have a machine theory assignment and I am adding the conditions of this assignment here as a picture. You choose the mechanism and write the necessary solutions for this mechanism.arrow_forwardQ41 (20 Marks) An ideal steam power plant works on regenerative cycle. Some steam (y1) is bled out between first and second stage and another portion (y2) is bled between second and third stages and feed the feed water heaters as shown in the following figures. In terms of enthalpies determine (1) y1 (2) y2 (3)the work at the first turbine (4) the work at the second turbine (5) the work at the third turbine (6) the work at the pump (FP1) (7) the work at the pump (FP2) (8) the work at the pump (CEP) (9) the heat received at the boiler (10) the rejected heat Boiler NY ST1 ST2 ST3 TI 52 Condenser CFWH OFWH 11 www 12 10 CEP FP FParrow_forwardDONT USE ARTIFICIAL INTELLIGENCEarrow_forward
- Q2] (20 Marks) A steam turbine with one open feed water heater (OFWH) as shown in the following figure. In terms of enthalpies and y determine: 1- Work of HPT 2- Work of LPT 3- Work at Pump1 4- Work at Pump2 5-The heat added at the boiler 6- The quantity (y) in terms of enthalpies 7-Heat extracted from condenser 5 Boiler 2岁 3 OFWH 9 Pump2 HPT LPT 8 Pump1 O Condenserarrow_forward11.2 Boxes A and B are at rest on a conveyer belt that is initially at rest. The belt suddenly starts in an upward direction so that slipping instantly occurs between the belt and the boxes. The kinetic friction coefficients between the belt and the boxes are μk,A = 0.3 and μk,B = 0.32. Determine the initial acceleration of each box. Will the blocks stay together, or separate? 80 lb 100 lb A B 15° Hint: to see if the boxes stay together or separate, first assume they separate, and see if their resulting motion (acceleration) validates that assumption. If the their motion is not consistent with the assumption of separation, then they must stay together.arrow_forwardAn ideal gas is enclosed in a cylinder which has a movable piston. The gas is heated, resulting in an increase in temperature of the gas, and work is done by the gas on the piston so that the pressure remains constant. a) Is the work done by the gas negative, positive or zero? b) From a microscopic view, how is the internal energy of the gas molecules affected? c) Is the heat less than, greater than or equal to the work? Explain you answer.arrow_forward
- I need to adapt a real-life system to this assignment. It doesn't need to be a very complicated system. I am a senior mechanical engineering student. I need help with my mechanical theory homeworkarrow_forwardstate all the formulae associated with adiabatic processarrow_forwardDesign a Moore type synchronous state machine with three external inputs A1, A2, A3 and one output signal F. The output F goes to 1 when A1.A2.-A3 = 1 at the next system timing event. The output F stays at 1 as long as A3=0; otherwise, the output goes to 0. (Note: use a positive edge-triggered D flip-flop in the design) Write a VHDL code to describe the implementation of one-digit decimal counter using PROCESS.arrow_forward
- State all the formulae associated with the Isothermal Process.arrow_forward: +0 العنوان solle не Am 4 A pump draws water through a 300-mm diameter cast iron pipe, 15m long from a reservoir in which the water surface is 4.5 m higher than the pump and discharges through a 250- mm diameter cast iron, 75 m long, to an elevated tank in which the water surface is 60 m higher than the pump. Q=0.25 m³/s. Considering f-0.02 and the coefficients for minor head losses (k entrance 0.5, k bend 0.35, and K exit -0.5), compute the power of the pump. ۳/۱ ۲/۱ 4.5 m Kentrance 300 mm dia. 15 m Length 250 mm dia. 75 m Length kpend kexit 60 m ostlararrow_forwardA 100 m length of a smooth horizontal pipe is attached to a large reservoir. A attached to the end of the pipe to pump water into the reservoir at a volume flow rate of 0.01 m³/s. What pressure (gage) must the pump produce at the pipe to generate this flow rate? The inside diameter of the smooth pipe is 150mm. Dynamic Viscosity of water is 1*103 Kg/(m.s). K at the exit of the pipe is 1. pump 10 m D=150mm L= 100 m- Pumparrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Solids: Lesson 53 - Slope and Deflection of Beams Intro; Author: Jeff Hanson;https://www.youtube.com/watch?v=I7lTq68JRmY;License: Standard YouTube License, CC-BY