Chapter 10, Problem 10.3.1P

A propped cantilever steel beam is constructed from a W12 × 35 section. The beam is loaded by its self-weight with intensity q. The length of the beam is 1L5 ft. Let E = 30,000 ksi.

1. Calculate the reactions at joints A and B.

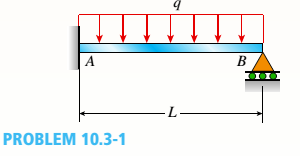
Find the location of zero moment within span AB.

Calculate the maximum deflection of the beam and the rotation at joint B.

  

To determine

The reaction at joint A and B.

Answer to Problem 10.3.1P

  $\begin{array}{l}{R}_B=0.151kips\\ R_A=0.252kips\\ M_A=0.57kip-f\end{array}$

Explanation of Solution

Given information:

  

  $\begin{array}{l}\text{for W12}\times \text{35,}\\ \text{q=35 }\left\{\text{(from appendix f(a)}\right\}\\ L=11.5ft\\ E=30000ksi\end{array}$

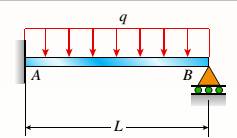
The first step is to consider the equilibrium condition of the entire beam, express the other two reaction in term of $R_B$ .

We have,

  $\begin{array}{l}{R}_A=qL-R_B,\\ M_A=\frac{q{L}^2}{2}-R_{B}L\end{array}$

Bending moment,

Consider a distance x away from the fixed support.

  $M=R_{A}x-M_A-\frac{q{x}^2}{2}$

On substituting the values,

  $M=qLx-R_{B}x-\frac{q{L}^2}{2}+R_{B}L-\frac{q{x}^2}{2}$

The second order of differential equation of deflection curve becomes,

  $El{v}^{″}=M=qLx-R_{B}x-\frac{q{L}^2}{2}+R_{B}L-\frac{q{x}^2}{2}$

On two successive integrations, we obtain the equation of slope and deflection:

Slope:

  $El{v}^{\prime }=\frac{qL{x}^2}{2}-\frac{R_B{x}^2}{2}-\frac{q{L}^{2}x}{2}+R_{B}Lx-\frac{q{x}^3}{6}+c_1$

Deflection:

  $Elv=\frac{qL{x}^3}{6}-\frac{R_B{x}^3}{6}-\frac{q{L}^2{x}^2}{4}+\frac{R_{B}L{x}^2}{2}-\frac{q{x}^4}{24}+c_{1}x+c_2$

These equations contain three unknown quantities:

  $\left(c_1,c_2,R_B\right)$

Applying boundary conditions,

  $\begin{array}{l}{v}^{\prime }(0)=0\therefore c_1=0\\ v(0)=0\therefore c_2=0\end{array}$

  $\begin{array}{l}{R}_B=\frac{3qL}{8}=0.151kips\\ \therefore R_A=\frac{5qL}{8}=0.252kips\\ M_A=\frac{q{L}^2}{2}-R_{B}L=0.57kip-ft\end{array}$

To determine

The location of zero moment within span AB.

Answer to Problem 10.3.1P

  $x_{zero}=2.875ft$

Explanation of Solution

X zero means, the position at which the value of bending moment is zero.

The bending moment is zero at:

  $\begin{array}{l}{x}_{zero}=\frac{L}{4}\\ x_{zero}=\frac{11.5}{4}=2.875ft\end{array}$

To determine

The maximum deflection of beam and the rotation at joint B.

Answer to Problem 10.3.1P

  ${\delta }_{\max }=6.67\times {10}^{-4}in$

  ${\text{θ}}_B=1.86\times {10}^{-5}rad$

Explanation of Solution

Given information:

  $\begin{array}{l}\left\{\text{(from appendix f(a)}\right\}\\ \text{q=35lb}\\ I=285i{n}^4\\ L=11.5ft\\ E=30000ksi\end{array}$

Maximum deflection:

  ${\delta }_{\max }=\frac{q{x}^2}{4LEI}=6.67\times {10}^{-4}in$

Rotation at joint B,

  ${\text{θ}}_B=\frac{q{L}^3}{24EI}$

  ${\text{θ}}_B=1.86\times {10}^{-5}rad$