
Concept explainers
Solve the preceding problem by integrating the differential equation of the deflection curve.
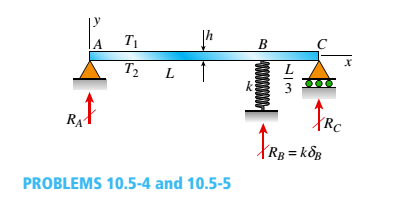
(a)
The reactions for beam at all supports.
Answer to Problem 10.5.5P
The reaction at support
The reaction at support
The reaction at support
Explanation of Solution
Given information:
The two spans of beam are
Write the Expression for force equilibrium in vertical direction.
Here, reaction produced at
Write the expression for moment about point
Here,
Write the expression for moment about point
Here,
Write the expression for double order differential equation for the deflection curve when any value between
Here, double order differential of deflection curve is
Write the expression for single order derivative of deflection curve when any value between
Here, length at which deflection has to be calculate is
Write the expression for deflection curve when any value between
Here, deflection at a point
Write the expression for first boundary condition.
Here, deflection when
Write the expression for second boundary condition when
Here, single order differential of deflection curve from the loads left to spring is
Write the expression for third boundary condition when
Write the expression for fourth boundary condition.
Here, deflection when
Write the expression for differential equation for the deflection curve when any value between
Write the expression for single order derivative of deflection curve when any value between
Write the expression for deflection curve when any value between
Write the expression for compatibility Equation for spring when
Substituted
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Solve Equation (XXIII) and Equation (XXIV).
Substitute
Conclusion:
The reaction at support
The reaction at support
The reaction at support
(b)
The reactions at all the supports when value of
Answer to Problem 10.5.5P
The reaction at support
The reaction at support
The reaction at support
Explanation of Solution
Take limit of
Take limit of
Take limit of
Conclusion:
The reaction at support
The reaction ay support
The reaction at support
Want to see more full solutions like this?
Chapter 10 Solutions
Mechanics of Materials (MindTap Course List)
- Solve this problem and show alll of the workarrow_forwardI need drawing solution,draw each one by one no Aiarrow_forwardQu. 17 Compute linear density values for [100] for silver (Ag). Express your answer in nm''. . Round off the answer to three significant figures. Qu. 18 Compute linear density value for [111] direction for silver (Ag). Express your answer in nm'. Round off the answer to three significant figures. Qu. 19 Compute planar density value for (100) plane for chromium (Cr). Express your answer in nm?. Round off the answer to two significant figures. Qu. 20 Compute planar density value for (110) plane for chromium (Cr). Express your answer in nm ≥ to four significant figures. show all work please in material engineeringarrow_forward
- Large wind turbines with a power capacity of 8 MW and blade span diameters of over 160 m areavailable for electric power generation. Consider a wind turbine with a blade span diameter of 120m installed at a site subjected to steady winds at 8.25 m/s. Taking the overall efficiency of thewind turbine to be 33 percent and the air density to be 1.25 kg/m3, determine the electric powergenerated by this wind turbine. Also, assuming steady winds of 8.25 m/s during a 24-h period,determine the amount of electric energy and the revenue generated per day for a unit price of$0.08/kWh for electricity.arrow_forwardThe basic barometer can be used to measure the height of a building. If the barometric readingsat the top and at the bottom of a building are 672 and 696 mmHg, respectively, determine theheight of the building. Take the densities of air and mercury to be 1.18 kg/m3 and 13,600 kg/m3,respectivelyarrow_forwardA 7.25-hp (shaft) pump is used to raise water to an elevation of 17 m. If the mechanical efficiencyof the pump is 84 percent, determine the maximum volume flow rate of water.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
