Materials for Civil and Construction Engineers (4th Edition)
4th Edition
ISBN: 9780134320533
Author: Michael S. Mamlouk, John P. Zaniewski
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 1, Problem 1.16QP
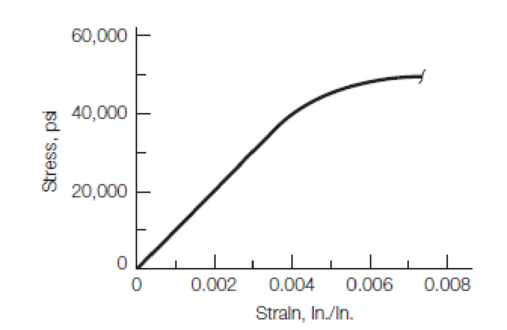
The stress–strain relationship shown in Figure P1.16 was obtained during the tensile test of an aluminum alloy specimen.
Determine the following:
a. Young’s modulus within the linear portion
b. Tangent modulus at a stress of 45,000 psi
c. Yield stress using an offset of 0.002 strain
d. If the yield stress in part c is considered failure stress, what is the maximum working stress to be applied to this material if a factor of safety of 1.5 is used?
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule05:06
Students have asked these similar questions
The prestressed concrete girder is made from plain
stone concrete and four -in. cold form steel reinforcing
rods. Determine the dead weight of the girder per foot of its
length.
8 in.
6 in.
20 in.
6 in.
8 in.
4 in. 6 in. 4 in.
The floor of a building, shown in Fig. (a), is subjected to a uniformly distributed load of 3.5 kPa over its surface area.
Determine the loads acting on all the members of the floor system.
AI
Column
Floor beam
B
Slab
C
D
3 at 4 m
= 12 m
Floor beam
E
F
Girder
GT
-9 m.
(a) Framing Plan
Commercial trucks begin to arrive at a seaport entry plaza at 7:50 A.M., at the rate of λ(t) = 6.3 – 0.25t[λ(t) is in veh/min and t is in minutes]. The plaza opens at 8:00 A.M. For the first 10 minutes, one processing booth is open. After the first 10 minutes until the queue clears, two processing booths are open. Each booth processes trucks at a uniform rate of two per minute. What is the average delay per vehicle, the maximum queue length, and the average queue length?
Chapter 1 Solutions
Materials for Civil and Construction Engineers (4th Edition)
Ch. 1 - State three examples of a static load application...Ch. 1 - A material has the stressstrain behavior shown in...Ch. 1 - A tensile load of 50.000 lb is applied to a metal...Ch. 1 - A tensile load of 190 kN is applied to a round...Ch. 1 - A cylinder with a 6.0 in. diameter and 12.0 in....Ch. 1 - A metal rod with 0.5 inch diameter is subjected to...Ch. 1 - A rectangular block of aluminum 30 mm 60 mm 90...Ch. 1 - A plastic cube with a 4 in. 4 in. 4 in. is...Ch. 1 - A material has a stressstrain relationship that...Ch. 1 - On a graph, show the stressstrain relationship...
Ch. 1 - The rectangular block shown in Figure P1.11 is...Ch. 1 - The rectangular metal block shown in Figure P1.11...Ch. 1 - A cylindrical rod with a length of 380 mm and a...Ch. 1 - A cylindrical rod with a radius of 0.3 in. and a...Ch. 1 - A cylindrical rod with a diameter of 15.24 mm and...Ch. 1 - The stressstrain relationship shown in Figure...Ch. 1 - A tension test performed on a metal specimen to...Ch. 1 - An alloy has a yield strength of 41 ksi, a tensile...Ch. 1 - Prob. 1.21QPCh. 1 - Figure P1.22 shows (i) elasticperfectly plastic...Ch. 1 - An elastoplastic material with strain hardening...Ch. 1 - A brace alloy rod having a cross sectional area of...Ch. 1 - A brass alloy rod having a cross sectional area of...Ch. 1 - A copper rod with a diameter of 19 mm, modulus of...Ch. 1 - A copper rod with a diameter of 0.5 in., modulus...Ch. 1 - Define the following material behavior and provide...Ch. 1 - An asphalt concrete cylindrical specimen with a...Ch. 1 - What are the differences between modulus of...Ch. 1 - Prob. 1.33QPCh. 1 - A metal rod having a diameter of 10 mm is...Ch. 1 - What is the factor of safety? On what basis is its...Ch. 1 - Prob. 1.36QPCh. 1 - Prob. 1.37QPCh. 1 - A steel rod, which is free to move, has a length...Ch. 1 - In Problem 1.38, if the rod is snugly fitted...Ch. 1 - A 4-m-long steel plate with a rectangular cross...Ch. 1 - Estimate the tensile strength required to prevent...Ch. 1 - Prob. 1.42QPCh. 1 - Briefly discuss the variability of construction...Ch. 1 - In order to evaluate the properties of a material,...Ch. 1 - A contractor claims that the mean compressive...Ch. 1 - A contractor claims that the mean compressive...Ch. 1 - Prob. 1.47QPCh. 1 - Prob. 1.48QPCh. 1 - Prob. 1.49QPCh. 1 - Briefly discuss the concept behind each of the...Ch. 1 - Referring to the dial gauge shown in Figure P1.51,...Ch. 1 - Repeat Problem 1.51 using the dial gauge shown in...Ch. 1 - Measurements should be reported to the nearest...Ch. 1 - During calibration of an LVDT, the data shown in...Ch. 1 - During calibration of an LVDT, the data shown in...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
The beam AB is pin supported at A and supported by a cable BC. A separate cable CG is used to hold up the frame...
Mechanics of Materials (10th Edition)
In the circuit shown in Fig. P 7.26, both switches operate together; that is, they either open or close at the ...
Electric Circuits. (11th Edition)
102* The sum of seven interior angles ofa closed-polygon traverse each read to the nearest
3 ” is
$99 a 59 '39...
Elementary Surveying: An Introduction To Geomatics (15th Edition)
What is an algorithm?
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
The repetition operator () works with strings as well as with lists.
Starting Out with Python (4th Edition)
List the five major hardware components of a computer system.
Starting Out With Visual Basic (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Similar questions
- The floor system of a gymnasium consists of a 130-mm-thick concrete slab resting on four steel beams (A = 9100 mm²) that, in turn, are supported by two steel girders (A = 25600 mm²), as shown in Fig. 2.3. Determine the dead loads acting on beam BF and girder AD. 2.3 Beam BF Uniformly distributed load ㅋㅋ =28.6 (5) (180) + 77 (100) = 16.04 kN/m 16.04 kN/m B 80.2 kN F 80.2 kN.arrow_forwardTrucks begin to arrive at a truck weigh station (with a single scale) at 6:00 A.M. at a deterministic but time-varying rate of λ(t) = 4.3 − 0.22t [λ(t) is in veh/min and t is in minutes]. The departure rate is a constant 2 veh/min (time to weigh a truck is 30 seconds). When will the queue that forms be cleared, what will be the total delay, and what will be the maximum queue length?arrow_forwardhow many custom bricks of size 3 1/4 x 3 3/4arrow_forward
- How many custom bricks of size 3 1/4 x 3 3/4 x 11 7/8 inches are there per square foot of wall area when the mortar joint is 1/4arrow_forwardGiven a circular curve connecting 2 tangents that intersect at an angle of 55°. The PI is at thestation (948+50) and the design speed of the highway is 70 mi/h. Determine:(a) stations of the PC and PT(c) Deflection angles and chord lengths for the first, middle, and last chordsarrow_forwardA simple circular curve exists with a radius of 900 ft connects the tangents of a two-lanehighway that has a posted speed limit of 45 mph. The highway curve is not superelevated,e=0. A structure is proposed on land on the inside of the curve. Assume the road is on a levelgrade. Determine the minimum distance allowable between the proposed structure and thecenterline of the curve such that the current maximum safe speed of the curve would notneed to be reducedarrow_forward
- A +4.4% grade intersects with a -3.3% grade at a station (550+30) at an elevation of400 ft. If the design speed is 60 mi/h, determine:(a) the minimum length of the vertical curve using the rate of vertical curvature(b) the stations and elevations of the BVC and EVC(c) the tangent and curve elevations of BVC, full stations, and EVC(d) the station and elevation of the highest pointarrow_forwardDetermine the minimum length of a sag vertical curve if the grades are –3% and +4%. The design speed is 75 mi/h. State all assumptions used. Make sure to consider the following criteria: stopping sight distance, comfort, and general appearancearrow_forwardQuestion 6: Chlorine is widely used to purify municipal water supplies and to treat swimming pool waters. Suppose that the volume of a particular sample of Cl₂ gas is 8.70 L at 895 torr and 24°C. (a) How many grams of Cl₂ are in the sample? ⚫ Atomic mass of CI = 35.453 g/mol • Molar mass of Cl₂ = 2 x 35.453 = 70.906 g/mol Solution: Use the Ideal Gas Law: Step 1: Convert Given Values • Pressure: P = 895 torr → atm PV= = nRT 1 P = 895 × = 1.1789 atm 760 • Temperature: Convert to Kelvin: T24273.15 = 297.15 K • Gas constant: R = 0.0821 L atm/mol. K Volume: V = 8.70 L Step 2: Solve for n . PV n = RT n = (1.1789)(8.70) (0.0821)(297.15) 10.25 n = = 0.420 mol 24.405 Step 3: Calculate Mass of Cl₂ Final Answer: 29.78 g of Cl₂. mass nx M mass= (0.420)(70.906) mass= 29.78 garrow_forward
- Please solve the highlighted question.arrow_forward1. Design a PVC sanitary sewer collection system for the Village of Waffle (Figure P-17-24 B, shown below) by preparing a sewer design table similar to that shown in Example 19-2 and a profile drawing similar to Figure 19-13b B. You only need to show the calculations for the pipes running along Bacon Road and Eggs Road, starting at point F and ending at Point B in the figure below. Your design should comply with the requirements specified in Chapter 30 of the 10 States Standards for Wastewater. Use the following assumptions: 0 о о Average daily flow rate is the same as average daily water demand, 9.2 m³/hr Peaking factor for peak dry weather flow is 6.2 Peak wet weather flow is equal to the peak dry weather flow plus an assumption for infiltration and inflow at 40 L/d-mm-km of pipe DODO on Ro 450 m 28 m D. 150 m Apartments D 400 m D 200 m B 250 m 0 Dogs Road ROOD625 m -120 m Syrup River 120 m 100-Year flood Point Elevation Tank 137.0 m A 130.0 m B 122.0 m C 122.3 m D 122.6 m A D 300 m…arrow_forwardNeed helparrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Materials Science And Engineering Properties
Civil Engineering
ISBN:9781111988609
Author:Charles Gilmore
Publisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...
Civil Engineering
ISBN:9781337094740
Author:Segui, William T.
Publisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...
Civil Engineering
ISBN:9781337705028
Author:Braja M. Das, Nagaratnam Sivakugan
Publisher:Cengage Learning
Material Properties 101; Author: Real Engineering;https://www.youtube.com/watch?v=BHZALtqAjeM;License: Standard YouTube License, CC-BY