Chapter 8.3, Problem 29E

a.

To determine

To write:

An equation describing the number of hours per month each type of plane should be rented if the flight school is to meet its goal.

Answer to Problem 29E

The equation $60x+180y=9000$ represents the number of hours per month each type of plane should be rented.

Explanation of Solution

Given:

At a flight school, pilots in training can rent single-engine airplanes for $60 per hour and twin-engine airplanes for $180 per hour. The flight school’s goal is to take in $9000 in rental fee each month.

Calculation:

Let x represent number of hours for which single-engine airplanes were rented and y represent number of hours for which twin-engine airplanes were rented.

We have been given that pilots in training can rent single-engine airplanes for $60 per hour, so amount charged for x hours of single-engine airplanes would be 60x .

We have been given that pilots in training can rent twin-engine airplanes for $180 per hour, so amount charged for yhours of twin-engine airplanes would be 180x .

The total amount charged for renting all airplanes will be equal to $9000. We can represent this information in an equation as:

  $60x+180y=9000$

Therefore, the equation $60x+180y=9000$ represents the number of hours per month each type of plane should be rented.

b.

To determine

To graph:

An equation from part (a) using the intercepts.

Answer to Problem 29E

x -intercept: $(150,0)$

y -intercept: $(0,50)$

Explanation of Solution

Given:

At a flight school, pilots in training can rent single-engine airplanes for $60 per hour and twin-engine airplanes for $180 per hour. The flight school’s goal is to take in $9000 in rental fee each month.

Calculation:

To find x -intercept, we will substitute $y=0$ in our given equation and solve for xas shown below:

  $\begin{array}{l}60x+180y=9000\left(\text{Given equation}\right)\\ 60x+180(0)=9000\left(\text{Substituting }y=0\right)\\ 60x=9000\\ \frac{60x}{60}=\frac{9000}{60}\left(\text{Dividing both sides by 60}\right)\\ x=150\end{array}$

Therefore, the x -intercept of our given equation is $(150,0)$ .

To find y- intercept, we will substitute $x=0$ in our given equation and solve for yas shown below:

  $\begin{array}{l}60x+180y=9000\left(\text{Given equation}\right)\\ 60(0)+180y=9000\left(\text{Substituting }x=0\right)\\ 180y=9000\\ \frac{180y}{180}=\frac{9000}{180}\left(\text{Dividing both sides by 180}\right)\\ y=50\end{array}$

Therefore, the y -intercept of our given equation is $(0,50)$ .

Upon graphing our given equation, we will get our required graph as shown below:

  

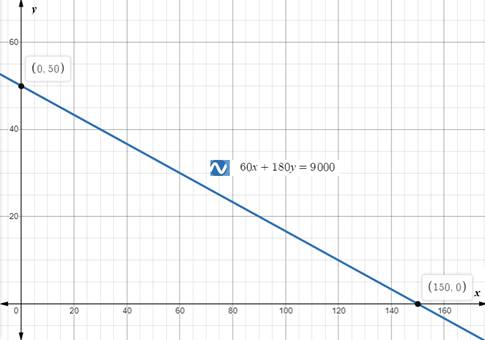
c.

To determine

To use:

Your graph to estimate how many hours the single-engine plane must be rented if the flight school is to meet its goal.

Answer to Problem 29E

The single-engine planes must be rented for 60 hoursif the flight school is to meet its goal.

Explanation of Solution

Given:

During one month, the twin-engine airplanes were rented for 30 hours.

Calculation:

Upon looking at our graph, we can see that the value of x is 60, when $y=30$ .

Therefore, the single-engine planes must be rented for 60 hoursif the flight school is to meet its goal.

d.

To determine

To check:

Your answer to part $(\text{c})$ by writing and solving an equation.

Answer to Problem 29E

The answer to part $(\text{c})$ is correct.

Explanation of Solution

Given:

During one month, the twin-engine airplanes were rented for 30 hours.

Calculation:

To solve our given problem, we will substitute $y=30$ in equation $60x+180y=9000$ and solve for x as shown below:

  $\begin{array}{l}60x+180y=9000\\ 60x+180(30)=9000\\ 60x+5400=9000\\ 60x+5400-5400=9000-5400\\ 60x=3600\\ \frac{60x}{60}=\frac{3600}{60}\\ x=60\end{array}$

Since we got same value, therefore, the single-engine planes must be rented for 60 hoursif the flight school is to meet its goal.