
Concept explainers
a.
As a skydiver falls, does the atmospheric pressure increase or decrease? Does the reading on skydiver’s altimeter increase or decrease?
a.
Answer to Problem 24E
The atmospheric pressure will increase as a skydiver will fall.
The reading on skydiver’s altimeter will decrease.
Explanation of Solution
Given:
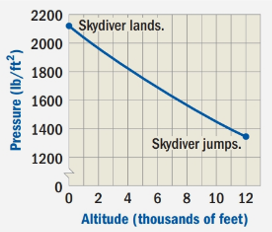
A skydiver uses an altimeter to track altitude so that he or she knows when to open the parachute. The altimeter determines altitude by measuring changes in atmospheric pressure. The graph below shows how pressure varies with altitude as a skydiver falls from 12,000 feet to ground level. (The elevation of the ground is assumed to be 0 feet with respect to sea level.)
Calculation:
Upon looking at our given graph, we can see that x -axis represents altitude of a skydiver in thousands of feet and y -axis represents atmospheric pressure in pounds per square feet.
Since the ground level will be at
Therefore, the atmospheric pressure will increase as a skydiver will fall.
Since the altimeter determines altitude, so reading on skydiver’s altimeter will decrease.
b.
To describe:
The domain and range of the relation represented by the graph.
b.
Answer to Problem 24E
The domain of the relation represented by the graph is
The range of the relation represented by the graph is
Explanation of Solution
Given:
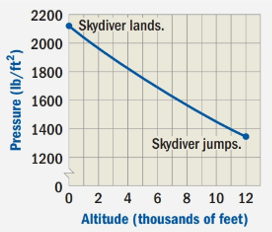
A skydiver uses an altimeter to track altitude so that he or she knows when to open the parachute. The altimeter determines altitude by measuring changes in atmospheric pressure. The graph below shows how pressure varies with altitude as a skydiver falls from 12,000 feet to ground level. (The elevation of the ground is assumed to be 0 feet with respect to sea level.)
Calculation:
Upon looking at our given graph, we can see that x values on our graph goes from
We can also see that y values on our graph goes from
c.
Is the relation a function? Explain.
c.
Answer to Problem 24E
The given relation is a function as the graph passes vertical line test.
Explanation of Solution
Given:
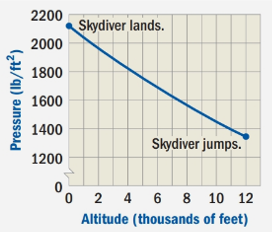
A skydiver uses an altimeter to track altitude so that he or she knows when to open the parachute. The altimeter determines altitude by measuring changes in atmospheric pressure. The graph below shows how pressure varies with altitude as a skydiver falls from 12,000 feet to ground level. (The elevation of the ground is assumed to be 0 feet with respect to sea level.)
Calculation:
Upon looking at our given graph, we can see that any verticalwill not intersect our graph more than one place. Therefore, the given relation is a function.
d.
Some altimeters can sound an alarm warning a skydiver to open the parachute when the altitude falls to a certain level. If the alarm is set to go off at an altitude of 3000 feet, approximately what atmospheric pressure will trigger the alarm?
d.
Answer to Problem 24E
An atmospheric pressure of 1900 pounds per square feet will trigger the alarm.
Explanation of Solution
Given:
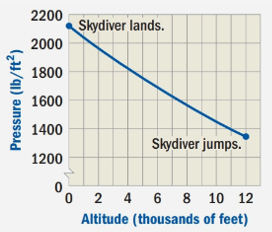
A skydiver uses an altimeter to track altitude so that he or she knows when to open the parachute. The altimeter determines altitude by measuring changes in atmospheric pressure. The graph below shows how pressure varies with altitude as a skydiver falls from 12,000 feet to ground level. (The elevation of the ground is assumed to be 0 feet with respect to sea level.)
Calculation:
To solve our given problem, we need to check the value of y , when
Upon looking at our given graph, we can see that the value of y is 1900 at
Chapter 8 Solutions
Holt Mcdougal Larson Pre-algebra: Student Edition 2012
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics (13th Edition)
Introductory Statistics
Pre-Algebra Student Edition
Elementary Statistics: Picturing the World (7th Edition)
- Round as specified A) 257 down to the nearest 10’s place B) 650 to the nearest even hundreds, place C) 593 to the nearest 10’s place D) 4157 to the nearest hundreds, place E) 7126 to the nearest thousand place arrow_forwardEstimate the following products in two different ways and explain each method  A) 52x39 B) 17x74 C) 88x11 D) 26x42arrow_forwardFind a range estimate for these problems A) 57x1924 B) 1349x45 C) 547x73951arrow_forward
- Draw the image of the following figure after a dilation centered at the origin with a scale factor of 14 退 14 12- 10 5- + Z 6 的 A X 10 12 14 16 18 G min 3 5arrow_forwardkofi makes a candle as a gift for his mom. The candle is a cube with a volume of 8/125 ft cubed. Kofi wants to paint each face of the candle exepct for the bottom. what is the area he will paint?arrow_forward10 6 9. 8 -7- 6. 5. 4- 3. 2 1- -1 0 -1 2 3 4 ·10 5 6 7 00 8 6 10arrow_forward
- Week 3: Mortgages and Amortiza X + rses/167748/assignments/5379530?module_item_id=23896312 11:59pm Points 10 Submitting an external tool Gider the following monthly amortization schedule: Payment # Payment Interest Debt Payment Balance 1 1,167.34 540.54 626.80 259,873.20 2 1,167.34 539.24 628.10 259,245.10 3 1,167.34 With the exception of column one, all amounts are in dollars. Calculate the annual interest rate on this loa Round your answer to the nearest hundredth of a percent. Do NOT round until you calculate the final answer. * Previous a Earrow_forwardCafé Michigan's manager, Gary Stark, suspects that demand for mocha latte coffees depends on the price being charged. Based on historical observations, Gary has gathered the following data, which show the numbers of these coffees sold over six different price values: Price Number Sold $2.70 765 $3.50 515 $2.00 990 $4.30 240 $3.10 325 $4.00 475 Using simple linear regression and given that the price per cup is $1.85, the forecasted demand for mocha latte coffees will be cups (enter your response rounded to one decimal place).arrow_forwardGiven the correlation coefficient (r-value), determine the strength of the relationship. Defend your answersarrow_forward
- ??!!arrow_forwardrections: For problem rough 3, read each question carefully and be sure to show all work. 1. Determine if 9(4a²-4ab+b²) = (6a-3b)² is a polynomial identity. 2. Is (2x-y) (8x3+ y³) equivalent to 16x4-y4? 3. Find an expression that is equivalent to (a - b)³. Directions: For problems 4 and 5, algebraically prove that the following equations are polynomial identities. Show all of your work and explain each step. 4. (2x+5)² = 4x(x+5)+25 5. (4x+6y)(x-2y)=2(2x²-xy-6y²)arrow_forwardName: Mussels & bem A section of a river currently has a population of 20 zebra mussels. The population of zebra mussels increases 60 % each month. What will be the population of zebra mussels after 2 years? 9 10 # of months # of mussels 1 2 3 4 5 6 7 8 o Graph your data. Remember to title your graph. What scale should be used on the y-axis? What scale should be used on the x-axis? Exponential Growth Equation y = a(1+r)*arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





