Chapter 8, Problem 12RE

Solution

To find: The center, vertices and foci of the identified conic $\frac{y^2}{36}+\frac{{\left(x+6\right)}^2}{20}=1$ and sketch its graph.

Ellipse. Center is $\left(-6,0\right)$ ,vertices : $\left(-6,6\right)$ and $\left(-6,-6\right)$ ; foci: $\left(-6,4\right)$ and $\left(-6,-4\right)$ .

Given information:

Equation of conic: $\frac{y^2}{36}+\frac{{\left(x+6\right)}^2}{20}=1$

Formula used:

The standard equation of the hyperbola is $\frac{{\left(y-k\right)}^2}{a^2}+\frac{{\left(x-h\right)}^2}{b^2}=1$

Center is $\left(h,k\right)$

Foci is $\left(h,k\pm c\right)$

Vertices is $\left(h,k\pm a\right)$

Pythagorean relation: $a^2=b^2+c^2$

Calculation:

The equation $\frac{y^2}{36}+\frac{{\left(x+6\right)}^2}{20}=1$ is of the form of standard equation of the hyperbola $\frac{{\left(y-k\right)}^2}{a^2}-\frac{{\left(x-h\right)}^2}{b^2}=1$

Substitute $-6$ for $h$ and $0$ for $k$ in the center formula.

Center is $\left(-6,0\right)$

Compare the equation with the standard equation of the hyperbola.

  $\begin{array}{l}{a}^2=36\\ a=6\\ b^2=20\end{array}$

Take square root on both sides of the equation.

  $\begin{array}{c}b=\sqrt{20}\\ =\sqrt{5\times 4}\\ =2\sqrt{5}\end{array}$

Substitute $36$ for $a^2$ and $20$ for $b^2$ in the Pythagorean relation.

  $\begin{array}{c}{c}^2=36-20\\ =16\end{array}$

Take square root on both sides of the equation.

  $\begin{array}{c}c=\sqrt{16}\\ =4\end{array}$

Substitute $-6$ for $h$ , $4$ for $c$ and $0$ for $k$ in the foci formula.

Therefore, foci is

  $\begin{array}{l}\left(-6,4+0\right)\\ \left(-6,4\right)\\ \left(-6,-4+0\right)\\ \left(-6,-4\right)\end{array}$ .

Substitute $-6$ for $h$ , $0$ for $k$ and $6$ for $a$ in the vertices formula.

Therefore, vertices are

  $\begin{array}{l}\left(-6,0+6\right)\\ \left(-6,6\right)\\ \left(-6,0-6\right)\\ \left(-6,-6\right)\end{array}$ .

Draw the graph as follows:

  

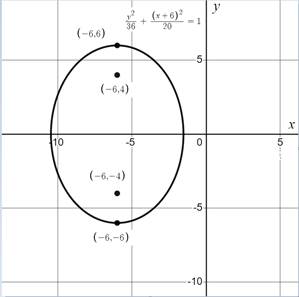
Hence, the given equation of conic is an ellipse. center is $\left(-6,0\right)$ ,vertices are $\left(-6,6\right)$ and $\left(-6,-6\right)$ and foci is $\left(-6,4\right)$ and $\left(-6,-4\right)$ .