
In Problems 17 to 20, find the Fourier sine transform of the function in the indicated problem, and write
Problem 10.
In Problems 3 to 12, find the exponential Fourier transform of the given
10.
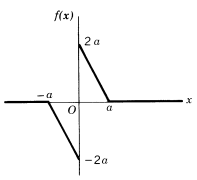
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Mathematical Methods in the Physical Sciences
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
STATISTICS F/BUSINESS+ECONOMICS-TEXT
A First Course in Probability (10th Edition)
Algebra and Trigonometry (6th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
- 4. 5. 6. Prove that p (gp) is a tautology using the laws of propositional logic. Prove that p((pVq) → q) is a tautology using the laws of propositional logic. Let us say a natural number n is ok if there are two natural numbers whose sum is n and whose product is n. (Convention: the natural numbers consist of 0, 1, 2,...) (a) Give a logical expression that means "n is ok". (b) Show that 0 and 4 are both ok. (c) Give a logical expression that means "every natural number is ok". (d) Give a logical expression that means "it is not the case that every number is ok". Push the negations into the expression as far as possible.arrow_forward7. Let E(x, y) be a two-variable predicate meaning "x likes to eat y", where the domain of x is people and the domain of y is foods. Write logical expressions that represent the following English propositions: (a) Alice doesn't like to eat pizza. (b) Everybody likes to eat at least one food. (c) Every student likes to eat at least one food other than pizza. (d) Everyone other than Alice likes to eat at least two different foods. (e) There are two different people that like to eat the same food.arrow_forward21. Determine for which values of m the function (x) = x™ is a solution to the given equation. a. 3x2 d²y dx² b. x2 d²y +11x dy - 3y = 0 dx dy dx2 x dx 5y = 0arrow_forward
- Question Find the following limit. Select the correct answer below: 1 2 0 4 5x lim sin (2x)+tan 2 x→arrow_forwardA quality characteristic of a product is normally distributed with mean μ and standard deviation σ = 1. Speci- fications on the characteristic are 6≤x≤8. A unit that falls within specifications on this quality characteristic results in a profit of Co. However, if x 8, the profit is -C2. Find the value ofμ that maximizes the expected profit.arrow_forwardA) The output voltage of a power supply is normally distributed with mean 5 V and standard deviation 0.02 V. If the lower and upper specifications for voltage are 4.95 V and 5.05 V, respectively, what is the probability that a power supply selected at random conform to the specifications on voltage? B) Continuation of A. Reconsider the power supply manufacturing process in A. Suppose We wanted to improve the process. Can shifting the mean reduce the number of nonconforming units produced? How much would the process variability need to be reduced in order to have all but one out of 1000 units conform to the specifications?arrow_forward
- A mechatronic assembly is subjected to a final functional test. Suppose that defects occur at random in these assemblies, and that defects occur according to a Poisson distribution with parameter >= 0.02. (a) What is the probability that an assembly will have exactly one defect? (b) What is the probability that an assembly will have one or more defects? (c) Suppose that you improve the process so that the occurrence rate of defects is cut in half to λ = 0.01. What effect does this have on the probability that an assembly will have one or more defects?arrow_forwardShow all steps. Correct answer is 1/2sec(theta) +Ccos(theta)arrow_forwardA random sample of 50 units is drawn from a production process every half hour. The fraction of non-conforming product manufactured is 0.02. What is the probability that p < 0.04 if the fraction non-conforming really is 0.02?arrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning


