
Concept explainers
For the circuit in Fig. 7.88, if
(a) Find R and C.
(b) Determine the time constant.
(c) Calculate the initial energy in the capacitor.
(d) Obtain the time it takes to dissipate 50 percent of the initial energy.
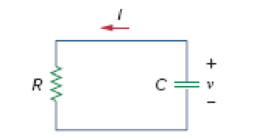
Figure 7.88
For Prob. 7.8.
(a)
Find the value of resistance R and capacitance C in the circuit.
Answer to Problem 8P
The value of resistance R in the circuit is
Explanation of Solution
Given data:
The voltage across the capacitor
The current flows through the circuit
Formula used:
Write the expression to find the voltage across the capacitor for a source-free RC circuit.
Here,
Write the expression to find the time constant for RC circuit.
Here,
R is the resistance of the resistor, and
C is the capacitance of the capacitor.
Write the expression to find the current through the capacitor.
Here,
Calculation:
Refer to Figure 7.88 in the textbook. In the circuit, the direction of current is given as leaving form the positive terminal the capacitor, therefore in equation (3), the current direction is taken as negative. The equation (3) becomes,
Substitute
Rearrange the equation to find capacitance C.
Substitute the unit F for
Compare the given voltage across the capacitor
Substitute
Substitute
Rearrange the equation to find resistance R.
Substitute the unit
Conclusion:
Thus, the value of resistance R in the circuit is
(b)
Calculate the value of time constant for the RC circuit.
Answer to Problem 8P
The value of time constant for the RC circuit is
Explanation of Solution
Given data:
Refer part (a),
The value of resistance is
The value of capacitance
Calculation:
Substitute
Substitute the units
Conclusion:
Thus, the value of time constant for the RC circuit is
(c)
Find the initial energy in the capacitor
Answer to Problem 8P
The initial energy in the capacitor
Explanation of Solution
Given data:
Refer part (a),
The value of capacitance
The initial voltage
Formula used:
Write the expression to find the initial energy in the capacitor.
Calculation:
The voltage across the capacitor,
Compare the equation (10) and (1) for the initial voltage
Substitute
Substitute the unit
Convert the unit J to mJ.
Conclusion:
Thus, the initial energy in the capacitor
(d)
Find the time taken to dissipate 50 percent of the initial energy.
Answer to Problem 8P
The time taken to dissipate 50 percent of the initial energy is
Explanation of Solution
The energy in the capacitor to dissipate 50 percent of the initial energy is,
Substitute
Substitute the unit
Rearrange the equation as follows.
Take ln on both sides of the equation (14) to find the time t in seconds.
Rearrange the equation as follows.
Convert the unit s to ms.
Conclusion:
Thus, the time taken to dissipate 50 percent of the initial energy is
Want to see more full solutions like this?
Chapter 7 Solutions
EBK FUNDAMENTALS OF ELECTRIC CIRCUITS
- Consider the lateral dynamics of a vectored thrust aircraft as described in Example 3.12. Show that the dynamics can be described using the following block diagram: Ꮎ r ալ -mg Σ J82 ע 1 X ms² + cs Use this block diagram to compute the transfer functions from u₁ to 0 and x and show that they satisfy Нои r Js² - mgr Js²' Hau₁ Js2 (ms2+cs)arrow_forwardConsider the system dx ax+u. dt Compute the exponential response of the system and use this to derive the transfer function from u to x. Show that when s = a, a pole of the transfer function, the response to the exponential input u(t) = est is x(t) = eat x(0) + teat. For solving the system with u = eat eat you can't use the transfer function because the denominator is zero. Try using the convolution integral solution with initial conditions set as x(t) = eat x (0) + fo g(t − T)u(T)dT - g(t) is the impulse response of the system.arrow_forwarddny dn-1y dn-1u dn-24 +a1 + + Any = bi +b₂- + +bnu. dtn dtn-1 dtn-1 dtn-2 a) Let be a root of the characteristic equation 1 sn+a1sn- + +an = : 0. Show that if u(t) = 0, the differential equation has the solution y(t) = e\t. b) Let к be a zero of the polynomial b(s) = b₁s-1+b2sn−2+ Show that if the input is u(t) equation that is identically zero. = .. +bn. ekt, then there is a solution to the differentialarrow_forward
- dny dn-1y dn-1u dn-24 +a1 + + Any = bi +b₂- + +bnu. dtn dtn-1 dtn-1 dtn-2 a) Let be a root of the characteristic equation 1 sn+a1sn- + +an = : 0. Show that if u(t) = 0, the differential equation has the solution y(t) = e\t. b) Let к be a zero of the polynomial b(s) = b₁s-1+b2sn−2+ Show that if the input is u(t) equation that is identically zero. = .. +bn. ekt, then there is a solution to the differentialarrow_forwardFor step a), use equations (2) to find the equation for the input impedance equations (2) are V1 = jwL1I1 + jwMI2 and V2 = jwMI1 + jwL2I2 equation for the input impedance: Z1 = V1/I1 = jwL1 + (wM)2/(jwL2 + ZL)arrow_forwardL (a) Find currents i, and b₂ 2 2 (b) Find the dependent source voltage given as Find voltages V, and (c) V₂ 5i2 (d) For each circuit element in the circuit and the two Sources, state whether they are ABSORBING OF SUPPYING Power and how much power is absorbed or Supplied. + V - 5A +lov- C/E₂ + C/E4 Vz い 5+2 + 1A C/E 5V + シュ 2A + 10Varrow_forward
- 4) A circuit is given as shown. (a) Find currents i, and i2. (b) Find the dependent source voltage given as 5i2 (c) Find voltages V, and V₂ 2 (d) For each circuit element in the circuit and the two Sources, State whether they are ABSORBING, OF SUPPLYING POWER and how much power is absorbed or supplied. + 10V - + 4 CIES C/E + V L₁ 4 1A Y T5A GE -5V + CIES iz 2A 2 52 2 +arrow_forwardDetermine the eigenvalues and eigenvectors of using A = ( 1 -3 3 3 -5 3 6-64 Gauss eliminationarrow_forward5) A circuit is given as shown (a) Find currents i₁, L2 and is . (6) Find voltages V, V2, V3 and Vy (c) For each circuit element in the circuit and the two sources, state whether they are ABSORBING SUPPLYING POWER and how much power is absorbed or supplied. + V₁ CIE, 1A +2V- C/E AS 1A + - 4A Vy+ CES CIES 2A4 + IOV +- + + V2 1 434 12V GVarrow_forward
- Determine the eigenvalues and eigenvectors of using Gauss A = -3 322 20 132 -3° 10 -2 4 eliminationarrow_forwardDetermine the eigenvalues and eigenvectors of 1-3 3 A = 3-53 6-64arrow_forward(6) Determine currents 41, 42, 43, Ly and is CE 5 4A A है C d 62 4A 23 (a) nodes: a, b, c, d, e, f (6) 1A E b C/E 25 Ly 5Aarrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





