Chapter 6.S, Problem 11P

a)

Summary Introduction

To determine: The control limits for the mean and range chart and the overall means

Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.

Answer to Problem 11P

Hence, the UCL for $\overline{x}$-chart is 10.00714in and LCL is 9.993865in. The UCL for R chart is 0.024323in and LCL is 0in. The overall means for $\overline{x}$-chart is 10.0005in and R chart is 0.0115in.

Explanation of Solution

Given information:

The following information is given:

Sample	Sample mean (in.)	Range (in.)
1	10.002	0.011
2	10.002	0.014
3	9.991	0.007
4	10.006	0.022
5	9.997	0.013
6	9.999	0.012
7	10.001	0.008
8	10.005	0.013
9	9.995	0.004
10	10.001	0.011
11	10.001	0.014
12	10.006	0.009

Twelve samples that contain five parts each were taken.

Calculate the average for sample and range:

Sample	Sample mean (in.)	Range (in.)
1	10.002	0.011
2	10.002	0.014
3	9.991	0.007
4	10.006	0.022
5	9.997	0.013
6	9.999	0.012
7	10.001	0.008
8	10.005	0.013
9	9.995	0.004
10	10.001	0.011
11	10.001	0.014
12	10.006	0.009
Total	120.006	0.138
Average	10.0005	0.0115

Working note:

Average for sample:

It is calculated by dividing the total of sample and number of samples. Hence, the value of $\overline{\overline{x}}$ is 10.0005.

$\begin{array}{c}\text{Average}=\frac{\text{Total of Sample}}{\text{Number of samples}}\\ =\frac{120.006}{12}\\ =10.0005\end{array}$

Average for range:

It is calculated by dividing the total of range and number of samples. Hence, the value of $\overline{R}$ is 0.0115.

$\begin{array}{c}\text{Average}=\frac{\text{Total of Sample}}{\text{Number of samples}}\\ =\frac{0.138}{12}\\ =0.0115\end{array}$

Determine the UCL and LCL for mean:

Formulae to calculate control limits:

$\text{UCL}=\overline{\overline{x}}+A\times \overline{R}$ (1)

$\text{LCL}=\overline{\overline{x}}-A\times \overline{R}$ (2)

Here, the overall mean $\overline{\overline{x}}=10.0005\text{in}\text{.}$, the average range $\overline{R}=0.0115\text{in}\text{.}$ and A₂ is the Mean factor derived from standard tables showing factors for computing control charts. Given the sample size of 5, the Mean factor ${\text{A}}_2=0.577$ for $\sigma =3$.

Substitute the values in equation (1) to determine the value of UCL as follows:

$\begin{array}{c}\text{UCL}=\overline{\overline{x}}+A\times \overline{R}\\ =10.0005\text{in}+0.577\times 0.0115\text{in}\text{.}\\ =\text{10}\text{.00714}\end{array}$

Hence, the UCL value is 10.00714.

Substitute the values in equation (2) to determine the value of LCL as follows:

$\begin{array}{c}\text{LCL}=\overline{\overline{x}}-A\times \overline{R}\\ =10.0005\text{in}\text{.}-0.577\times 0.0115\text{in}\text{.}\\ =\text{9}\text{.993865}\text{in}.\end{array}$

Hence, the LCL value is 9.993865.

Therefore for the $\overline{x}$ chart, the upper control limit is ${\text{UCL}}_{\overline{x}}=\text{10}\text{.00714}$ and the lower control limit is ${\text{LCL}}_{\overline{x}}=\text{9}\text{.993865}\text{in}$.

Determine the UCL and LCL for range:

Formulae to calculate control limits:

${\text{UCL}}_{\text{R}}={\text{D}}_{\text{4}}\times \overline{R}$ (3)

${\text{LCL}}_{\text{R}}={\text{D}}_3\times \overline{R}$ (4)

Here,

The average range is $\overline{R}=0.0115\text{in}\text{.}$

${\text{D}}_{\text{3}}$ refers to the lower range factor

${\text{D}}_{\text{4}}$ refers to the upper range factor

$\overline{R}$ refers to the average range

Substitute the values in equation (3) to determine the value of UCL as follows:

$\begin{array}{c}{\text{UCL}}_{\text{R}}={\text{D}}_{\text{4}}\times \overline{R}\\ =2.115\times 0.0115\text{in}\text{.}\\ =0.024323in.\end{array}$

Hence, the UCL value is 0.024323.

Substitute the values in equation (4) to determine the value of LCL as follows:

$\begin{array}{c}{\text{LCL}}_{\text{R}}={\text{D}}_3\times \overline{R}\\ =0\times 0.0115\text{in}\text{.}\\ =0\end{array}$

Hence, the LCL value is 0.

Therefore, for the R-chart, the upper control limit is ${\text{UCL}}_R=0.024323$ and the lower control limit is ${\text{LCL}}_R=0$.

b)

Summary Introduction

To plot: The values of sample means and ranges in the chart.

Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.

Answer to Problem 11P

Control chart has been plotted for sample means and ranges.

Explanation of Solution

Given information:

The following information is given:

Sample	Sample mean (in.)	Range (in.)
1	10.002	0.011
2	10.002	0.014
3	9.991	0.007
4	10.006	0.022
5	9.997	0.013
6	9.999	0.012
7	10.001	0.008
8	10.005	0.013
9	9.995	0.004
10	10.001	0.011
11	10.001	0.014
12	10.006	0.009

Twelve samples that contain five parts each were taken.

Plot the sample mean values in the $\overline{x}$ control chart where ${\text{UCL}}_{\overline{x}}=10.0005$ and ${\text{LCL}}_{\overline{x}}=9.993865$

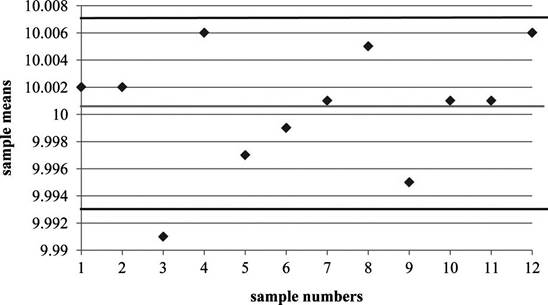
Note: Observe that sample 3 mean value is lower than the ${\text{LCL}}_{\overline{x}}=\text{9}\text{.993865}\text{in}.$

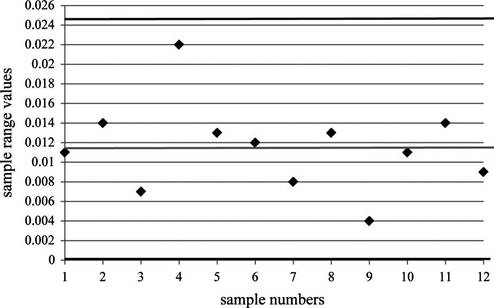
Plot the sample mean values in theR-control chart where ${\text{UCL}}_{\text{R}}=0.024323\text{in}$ and ${\text{LCL}}_{\text{R}}\text{=0}$

c)

Summary Introduction

To determine: Whether the process is in control

Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.

Answer to Problem 11P

Process is out of control during sample #3 in $\overline{x}$-chart.

Explanation of Solution

Given information:

The following information is given:

Sample	Sample mean (in.)	Range (in.)
1	10.002	0.011
2	10.002	0.014
3	9.991	0.007
4	10.006	0.022
5	9.997	0.013
6	9.999	0.012
7	10.001	0.008
8	10.005	0.013
9	9.995	0.004
10	10.001	0.011
11	10.001	0.014
12	10.006	0.009

Twelve samples that contain five parts each were taken.

Determine whether the process is in control:

Since, the mean for sample #3 is outside the control limits of the $\overline{x}$ control chart, it cannot be concluded that the process is in statistical control.

d)

Summary Introduction

To determine: Why the process is not in control

Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.

Explanation of Solution

Given information:

The following information is given:

Sample	Sample mean (in.)	Range (in.)
1	10.002	0.011
2	10.002	0.014
3	9.991	0.007
4	10.006	0.022
5	9.997	0.013
6	9.999	0.012
7	10.001	0.008
8	10.005	0.013
9	9.995	0.004
10	10.001	0.011
11	10.001	0.014
12	10.006	0.009

Twelve samples that contain five parts each were taken.

Determine why the process is not in control:

Further investigations are necessary to check whether the mean value of sample #3 is a freak incident outside the three sigma limits (which has a 0.27% probability). Perhaps 12 more samples can be drawn and examined whether such an incident occurs again. In case it happens again, the process needs to be examined in detail.