
Concept explainers
a)
To determine: The value of
Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.
a)
Answer to Problem 7P
Hence, the value of
Explanation of Solution
Given information:
The following information is given:
| Day | Mean (MM) | Range (MM) |
| 1 | 156.9 | 4.2 |
| 2 | 153.2 | 4.6 |
| 3 | 153.6 | 4.1 |
| 4 | 155.5 | 5 |
| 5 | 156.6 | 4.5 |
Determine the value of
| Day | Mean (MM) |
| 1 | 156.9 |
| 2 | 153.2 |
| 3 | 153.6 |
| 4 | 155.5 |
| 5 | 156.6 |
| Total | 775.8 |
Calculate the
It is calculated by dividing the sum of mean values and the number of days.
Hence, the value of
b)
To determine: The value of
Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.
b)
Answer to Problem 7P
Hence, the value of
Explanation of Solution
Given information:
The following information is given:
| Day | Mean (MM) | Range (MM) |
| 1 | 156.9 | 4.2 |
| 2 | 153.2 | 4.6 |
| 3 | 153.6 | 4.1 |
| 4 | 155.5 | 5 |
| 5 | 156.6 | 4.5 |
Determine the value of
| Day | Range (MM) |
| 1 | 4.2 |
| 2 | 4.6 |
| 3 | 4.1 |
| 4 | 5 |
| 5 | 4.5 |
| Total | 22.4 |
Calculate the
It is calculated by dividing the sum of mean values and the number of days.
Hence, the value of
c)
To plot: The UCL and LCL for
Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.
c)
Answer to Problem 7P
Hence, the value of UCL is 156.54mm and LCL is 153.78mm.
Explanation of Solution
Given information:
The following information is given:
| Day | Mean (MM) | Range (MM) |
| 1 | 156.9 | 4.2 |
| 2 | 153.2 | 4.6 |
| 3 | 153.6 | 4.1 |
| 4 | 155.5 | 5 |
| 5 | 156.6 | 4.5 |
Determine the UCL and LCL of
Formulae to determine Upper Control Limit and Lower Control Limit are given as follows:
Here, the overall mean is
Given the
Substitute the values in the given formulae:
Upper control limit can be calculated by adding the multiple of average range and mean factor with the overall mean.
Lower control limit can be calculated by subtracting the multiple of average range and mean factor from the overall mean.
Hence, upper control limit is 156.54mm and 153.78mm.
Plot the values:
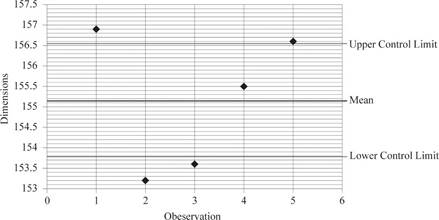
d)
To plot: The UCL and LCL for
Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.
d)
Answer to Problem 7P
Hence, the value of UCL is 7.96mm and LCL is 0.999mm.
Explanation of Solution
Given information:
The following information is given:
| Day | Mean (MM) | Range (MM) |
| 1 | 156.9 | 4.2 |
| 2 | 153.2 | 4.6 |
| 3 | 153.6 | 4.1 |
| 4 | 155.5 | 5 |
| 5 | 156.6 | 4.5 |
Determine the UCL and LCL of
Formulae to determine Upper Control Limit and Lower Control Limit are given as follows:
Here, the average range is
Given the sample size of 10 for
Substitute the values in the given formulae:
Upper control limit can be calculated by multiplying upper range factor and average range.
Upper control limit can be calculated by multiplying lower range factor and average range.
Hence, upper control limit is 7.96mm and 0.999mm.
Plot the values:
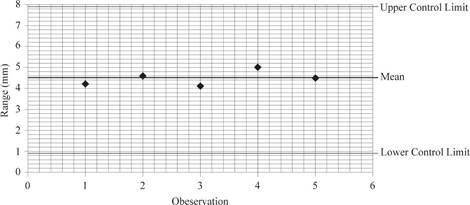
e)
To determine: The UCL and LCL for
Introduction: Control charts used to determine whether the process is under control or not. Attributes and variables are the factors under the control charts.
e)
Answer to Problem 7P
Hence, the value of UCL is 156.38mm and LCL is 153.62mm.
Explanation of Solution
Given information:
The following information is given:
| Day | Mean (MM) | Range (MM) |
| 1 | 156.9 | 4.2 |
| 2 | 153.2 | 4.6 |
| 3 | 153.6 | 4.1 |
| 4 | 155.5 | 5 |
| 5 | 156.6 | 4.5 |
Given the target value of the diameter
Here,
The target value of the diameter
Given the sample size of 10, the Mean factor
Substitute the values in the given formulae:
Upper control limit can be calculated by adding the multiple of average range and mean factor with the overall mean.
Lower control limit can be calculated by subtracting the multiple of average range and mean factor from the overall mean.
Hence, for the
Want to see more full solutions like this?
Chapter 6 Solutions
PRIN.OF OPERATIONS MANAGEMENT-MYOMLAB
- SIPOC Process Supplier Machines Quality Group Leader Double Output Customers Inputs Solutions End of batch Inspection verification Scrap evaluation Sampling Verification Batch complete Evaluation Completed Quality Group Leader Samplings verified Quality Samplings verified Quality Barcode programed Mechanic Parameters registered Quality Line verified Quality Line Verified Quality Second verification Barcode Parameters Line Inspection Second Line Inspection Lot and Expiration Date Quality Quality Mechanic Mechanic Quality Machines Quality Group Leader Quality Quality Quality Batch Verification Process complete Revision Review Sampling Verification Barcode Scanner Machine Parameters Line Clearance Line Clearance Machine Remove Lot Status Verification Close floor Final MFG Review Final QA Review Close Batch Machine removed Lot verified Floor closed MFG Reviewed Process reviewed Batch closed Mechanic Group Leader Quality Quality Quality Group Leaderarrow_forwardAn assessment of gender leadership and corporate culture.Kindly provide the following, citing it using in-text referencing: • A thorough exploration of gender dynamics and concepts.• Creating a clear plan to address gender bias and promote inclusive leadership.• An examination of female leadership dynamics and their impact on performance. • Comprehensive justification behind the proposal.arrow_forwardAssessment of Strategic Leadership and Global Context Provide the below in detail:· A comprehensive analysis of the current strategy,· Develop a new comprehensive strategic leadership framework that tackles the challenges of leading a global company while balancing global standards and responding to local context and challenges.· Justify a framework by drawing on and applying relevant theories of strategic leadership and global management.· It needs substantial depth and detail.· Conduct a critical evaluation of strategic leadership in a global context.arrow_forward
- Assessing Leadership Ethics and Cross-cultural DiversityProvide the below with in-cite text referencing:- Investigate ethical issues and how they influence diversity and cross-cultural leadership.• Develop an ethical decision-making model that addresses cross-cultural concerns in emerging markets, such as Africa.· Conduct comprehensive analysis and modelling if necessary.- Provide a thorough ethical analysis that considers cross-cultural issues.· Careful evaluation of potential outcomes.- The proposed ethical decision-making technique is both novel and defendable.· Promoting diversity and recognising cross-cultural differences.arrow_forwardNeed help, have no idea where to start and love help upon a paper idea with no AI and soemthing original please.arrow_forwardAbout the Assignment In this course, you learned how a business chooses a positioning strategy in the marketplace and focuses on these areas by evaluating management's use of production types, creating effective productivity, and analyzing the competitiveness of production. Now you will choose a retail organization and propose a positioning marketing strategy that analyzes the organizational management decisions related to any competitiveness of cost, quality, flexibility, speed, innovation, and/or service. Prompt Choose an organization that focuses on one of these areas in the market: competitiveness of cost, quality, flexibility, speed, innovation, and/or service. An example would be choosing ALDI or LIDL. Their cost marketing positioning strategy is providing customers with international goods for a lower price and, in turn, saving business fees by not providing bagging products for free. (This is just an example. Do not use this example for your project.) Use the following steps…arrow_forward
- Can you guys help me with this? Thank you! The project is Terminal 1 at JFK International Airport Here's what need to do: Time Content: What was the estimated time of the project; what was the final time (or the estimated date) of the project; what are the major contributing factors for the disparity? (Please make sure all the information here can be present around 2 minutes) Risk management content: Discuss a major risk management event that affected the project. while researching if any team member finds an interesting risk management event *Include sources that you have the information when go over these 2 parts above.arrow_forwardI only need help with part C. Please and thank you :) ANSWERED: Gracie recorded the following times assembling a watch. Performance rating given is 95%. A) Average time of Gracie for the Operation? (round to three decimal places) ANSWER=0.107 B) normal time for this operation? (round to three decimal places) ANSWER=0.102 C) HELP PLEASE. "For a given personal allowance of 8% the standard time for the operation is how many minutes?" (round your answer to three decimal places)arrow_forwardGracie recorded the following times assembling a watch. Performance rating given is 95%. Average time of Gracie for the Operation? (round to three decimal places) normal time for this operation? (round to three decimal places)arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage, Foundations of Business (MindTap Course List)MarketingISBN:9781337386920Author:William M. Pride, Robert J. Hughes, Jack R. KapoorPublisher:Cengage Learning
Foundations of Business (MindTap Course List)MarketingISBN:9781337386920Author:William M. Pride, Robert J. Hughes, Jack R. KapoorPublisher:Cengage Learning Foundations of Business - Standalone book (MindTa...MarketingISBN:9781285193946Author:William M. Pride, Robert J. Hughes, Jack R. KapoorPublisher:Cengage Learning
Foundations of Business - Standalone book (MindTa...MarketingISBN:9781285193946Author:William M. Pride, Robert J. Hughes, Jack R. KapoorPublisher:Cengage Learning



