Calculus Volume 3
Calculus Volume 3
1st Edition
ISBN: 9781630182038
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax College.
Textbook Question
Book Icon
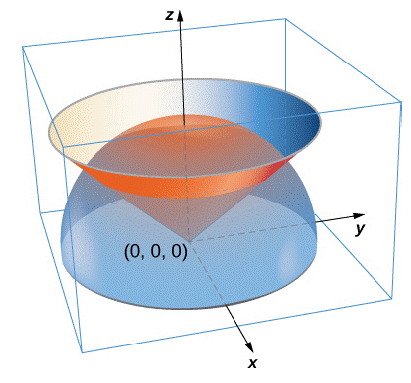
Chapter 6.6, Problem 320E

A lamina has the shape of a portion of sphere x 2 + y 2 + z 2 = a 2 that lies within cone z = x 2 + y 2 . Let S be the spherical shell centered at the origin with radius a, and let C be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Suppose the vertex angle of the cone is ϕ 0 , with 0 ≤ ϕ 0 ≤ π 2 . Determine the mass of that portion of the shape enclosed in the intersection of S and C . Assume δ ( x , y , z ) = x 2 y 2 z .

Chapter 6.6, Problem 320E, A lamina has the shape of a portion of sphere x2+y2+z2=a2 that lies within cone z=x2+y2 . Let S be

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 6.6, Problem 319E
Next
Chapter 6.6, Problem 321E
Students have asked these similar questions
Robbie Bearing Word Problems Angles name: Jocelyn date: 1/18 8K 2. A Delta airplane and an SouthWest airplane take off from an airport at the same time. The bearing from the airport to the Delta plane is 23° and the bearing to the SouthWest plane is 152°. Two hours later the Delta plane is 1,103 miles from the airport and the SouthWest plane is 1,156 miles from the airport. What is the distance between the two planes? What is the bearing from the Delta plane to the SouthWest plane? What is the bearing to the Delta plane from the SouthWest plane? Delta y SW Angles ThreeFourthsMe MATH 2
Find the derivative of the function. m(t) = -4t (6t7 - 1)6
Find the derivative of the function. y= (8x²-6x²+3)4

Chapter 6 Solutions

Calculus Volume 3

Ch. 6.1 - The domain of vector field F = F(x, y) is a set of...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...
Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - What is vector field F(x, y) with a value at (x,...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - Give a formula F(x, y) = M(x, y)i + N(x, y)j for...Ch. 6.1 - Is vector field F(x, y) = (P(x, y), Q(x, y)) =...Ch. 6.1 - Find a formula for vector field F(x, y) = M(x,,y)i...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - c(t) = (sin t. cos t, et); F(x,y,z)=y,x,zCh. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yj, G =...Ch. 6.1 - For the following exercises,...Ch. 6.1 - For the following exercises, let...Ch. 6.1 - For the following exercises, let...Ch. 6.2 - True or False? Line integral cf(x,y)dsis equal to...Ch. 6.2 - True or False? Vector functions r1= ti +t2j,...Ch. 6.2 - True or False? c(Pdx+Qdy)=c(PdxQdy)Ch. 6.2 - True or False? A piecewise smooth cuive C consists...Ch. 6.2 - True or False?If C is given by x(t) = t,y(t) = t,0...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - Evaluate the line integral of scalar function xy...Ch. 6.2 - Find yc2dx+(xy x 2)dy along C: y = 3x from C (0,...Ch. 6.2 - Find yc2dx+(xy x 2)dyalong C: y2= 9x from (0, 0)...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, find the flux. 87....Ch. 6.2 - For the following exercises, find the flux. 88....Ch. 6.2 - For the following exercises, find the flux. 89....Ch. 6.2 - For the following exercises, find the flux. 90....Ch. 6.2 - For the following exercises, find the flux. 91....Ch. 6.2 - Find the line integral of k c z 2dx+ydy+2ydz,where...Ch. 6.2 - A spring is made of a thin wire twisted into the...Ch. 6.2 - A thin wire is bent into the shape of a semicircle...Ch. 6.2 - An object moves in force field...Ch. 6.2 - Find the work done when an object moves in force...Ch. 6.2 - If an inverse force field F. is given by F(x, y,...Ch. 6.2 - David and Sandra plan to evaluate line integral...Ch. 6.3 - True or False? If vector field F is conservative...Ch. 6.3 - Trueor False? Function r(t) = a + t(b — a), where...Ch. 6.3 - True or False? Vector field F(x, y,z) = (y sinz)i...Ch. 6.3 - True or False?Vector field F(x,y,z)= yi + (x + z)j...Ch. 6.3 - Justify the Fundamental Theorem of Line Integrals...Ch. 6.3 - [T] Find cF.dr,,] where...Ch. 6.3 - [T] Evaluate line integral cF.dr, where...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - [T] Let F(x, y, z) = x2i + zsin(yz)j + y sin(yz)k....Ch. 6.3 - [T] Find line integral cF.dr,of vector field F(x,...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - Find the circulation and flux of field F=yi+xj...Ch. 6.3 - Compute ccosxcosydxsinxsinydy, where...Ch. 6.3 - Complete the proof of The Path Independence Test...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - easuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - ]Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - Find the counterclockwise circulation of field...Ch. 6.4 - Evaluate cy3dxx3y2dy,where C is the positively...Ch. 6.4 - Evaluate cy3dxx3dy,where C includes the two...Ch. 6.4 - Calculate cx2ydx+xy2dy,where C isa circle of...Ch. 6.4 - Calculate integral...Ch. 6.4 - Evaluate integral c( x 2+ y 2)dx+2xydy,where C is...Ch. 6.4 - Evaluate line integralc(ysin( y)cos( y)dx+2x sin...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - [T] Evaluate Green’s theorem using a computer...Ch. 6.4 - Evaluate c(x2y2xy+y2)ds,where C is the boundary of...Ch. 6.4 - Evaluate ( y+2)dx+( x1)dyc ( x1 ) 2+ ( y+2 )...Ch. 6.4 - 173. Evaluate xdx+ydy c x 2 + y 2 , . where C is...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - A particle starts at point (-2, 0), moves along...Ch. 6.4 - David and Sandra are skating on a frictionless...Ch. 6.4 - Use Green’s theorem to find the work done by force...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Evaluate line integral c y 2dx+x2dy,where C is...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c1+...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c(3y...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be a tiiangulai closed curve from (0, 0) to...Ch. 6.4 - Use Green’s theoiem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate cxydx+ x 3 y 3dy,...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let F(x,y)=(cos(x5))13y3i+13x3j.Find the...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be the boundary of square 0x,0y, traversed...Ch. 6.4 - Use Green’s theorem to evaluate line integral,...Ch. 6.4 - Use Green’s Theorem to evaluate integial...Ch. 6.4 - Use Green’s theorem in a plane to evaluate line...Ch. 6.4 - Calculate the outward flux of F = -xi + 2yj over a...Ch. 6.4 - 200. [T] Let C be circle x2+ y2= 4 oriented in the...Ch. 6.4 - Find the flux of field F = -xi + yj across x2+ y2...Ch. 6.4 - Let F = (y2— x2)i + (x2+y2)j, and let C be a...Ch. 6.4 - [T] Let C be unit circle x2+ y2 = 1 traversed once...Ch. 6.4 - [T] Find the outward flux of vector field F = xy2i...Ch. 6.4 - Consider region R bounded by parabolas y= x2and x...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - 233.w(x,y,z)=(x2+y2+z2)1/2Ch. 6.5 - 232.u(x,y,z)=ex(cosysiny)...Ch. 6.5 - 234.IfF(x,y,z)=2i+2xj+3ykCh. 6.5 - ...Ch. 6.5 - Find div F, given that F = f, where f(x,y,z)=xy3z2...Ch. 6.5 - 237. Find the divergence of F for vector field...Ch. 6.5 - Find the divergence of F for vector field...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r| and r =...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - Consider rotational velocity field v=0,10z,-10y....Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - wFor the following exercises, determine whether...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - wFor the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - wFor the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A paper cup has the shape of an inverted right...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - `For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - Draw the following vector fields. 431....Ch. 6 - Draw the following vector fields. 432....Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Evaluate the following integrals. 437....Ch. 6 - Evaluate the following integrals. 438. Cydx+xy2dy...Ch. 6 - Evaluate the following integrals. 439. Sxy2dS ,...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 444....Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 445....Ch. 6 - Use the divergence theorem to evaluate SFdS . 446....Ch. 6 - Use the divergence theorem to evaluate SFdS . 447....Ch. 6 - Find the amount of work perfumed by a 50 -kg woman...Ch. 6 - Find the total mass of a thin wire in the shape of...Ch. 6 - Find the total mass of a thin sheet in the shape...Ch. 6 - Use the divergence theorem to compute the value of...

Additional Math Textbook Solutions

Find more solutions based on key concepts
CHECK POINT 1 Write a word description of the set L = {a, b, c, d, e, f}.

Thinking Mathematically (6th Edition)

Squeeze Theorem Find the limit of the following sequences or state that they diverge. 58. {nsin3(n/2)n+1}

Calculus: Early Transcendentals (2nd Edition)

In Exercises 13–22, find the limit of each rational function (a) as and (b) as . Write or – where appropriate...

University Calculus: Early Transcendentals (4th Edition)

True or false: When limxaf(x) exists, it always equals f(a). Explain.

Calculus: Early Transcendentals (2nd Edition)

Two fair dice are rolled. What is the conditional probability that at least one lands on 6 given that the dice ...

A First Course in Probability (10th Edition)

31. Durations of Pregnancies The lengths of pregnancies are normally distributed with a mean of 268 days and a ...

Elementary Statistics (13th Edition)

Knowledge Booster
Background pattern image
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
SEE MORE TEXTBOOKS