Calculus Volume 3
Calculus Volume 3
1st Edition
ISBN: 9781630182038
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax College.
bartleby

Concept explainers

Arc Length
Arc length can be thought of as the distance you would travel if you walked along the path of a curve. Arc length is used in a wide range of real applications. We might be interested in knowing how far a rocket travels if it is launched along a parabolic…
Line Integral
A line integral is one of the important topics that are discussed in the calculus syllabus. When we have a function that we want to integrate, and we evaluate the function alongside a curve, we define it as a line integral. Evaluation of a function along…
Triple Integral
Examples:
bartleby

Videos

Textbook Question
Book Icon
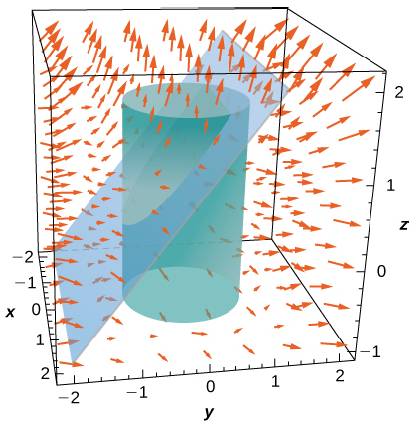
Chapter 6.6, Problem 286E

For the following exercises, evaluate ∫ ∫ s F ⋅ N d s for vector field F, where N is an outward normal vector to surface S.

286. F ( x , y , z ) = x 2 i + y 2 j + z 2 k , and S is the portion of plane z = y + 1 that lies inside cylinder x 2 + y 2 = 1 .

Chapter 6.6, Problem 286E, For the following exercises, evaluate sFNds for vector field F, where N is an outward normal

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 6.6, Problem 285E
Next
Chapter 6.6, Problem 287E
Students have asked these similar questions
2. Suppose f(x) = 3x² - 5x. Show all your work for the problems below.
write it down for better understanding please
1. Suppose F(t) gives the temperature in degrees Fahrenheit t minutes after 1pm. With a complete sentence, interpret the equation F(10) 68. (Remember this means explaining the meaning of the equation without using any mathy vocabulary!) Include units. (3 points) =

Chapter 6 Solutions

Calculus Volume 3

Ch. 6.1 - The domain of vector field F = F(x, y) is a set of...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...
Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - What is vector field F(x, y) with a value at (x,...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - Give a formula F(x, y) = M(x, y)i + N(x, y)j for...Ch. 6.1 - Is vector field F(x, y) = (P(x, y), Q(x, y)) =...Ch. 6.1 - Find a formula for vector field F(x, y) = M(x,,y)i...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - c(t) = (sin t. cos t, et); F(x,y,z)=y,x,zCh. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yj, G =...Ch. 6.1 - For the following exercises,...Ch. 6.1 - For the following exercises, let...Ch. 6.1 - For the following exercises, let...Ch. 6.2 - True or False? Line integral cf(x,y)dsis equal to...Ch. 6.2 - True or False? Vector functions r1= ti +t2j,...Ch. 6.2 - True or False? c(Pdx+Qdy)=c(PdxQdy)Ch. 6.2 - True or False? A piecewise smooth cuive C consists...Ch. 6.2 - True or False?If C is given by x(t) = t,y(t) = t,0...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - Evaluate the line integral of scalar function xy...Ch. 6.2 - Find yc2dx+(xy x 2)dy along C: y = 3x from C (0,...Ch. 6.2 - Find yc2dx+(xy x 2)dyalong C: y2= 9x from (0, 0)...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, find the flux. 87....Ch. 6.2 - For the following exercises, find the flux. 88....Ch. 6.2 - For the following exercises, find the flux. 89....Ch. 6.2 - For the following exercises, find the flux. 90....Ch. 6.2 - For the following exercises, find the flux. 91....Ch. 6.2 - Find the line integral of k c z 2dx+ydy+2ydz,where...Ch. 6.2 - A spring is made of a thin wire twisted into the...Ch. 6.2 - A thin wire is bent into the shape of a semicircle...Ch. 6.2 - An object moves in force field...Ch. 6.2 - Find the work done when an object moves in force...Ch. 6.2 - If an inverse force field F. is given by F(x, y,...Ch. 6.2 - David and Sandra plan to evaluate line integral...Ch. 6.3 - True or False? If vector field F is conservative...Ch. 6.3 - Trueor False? Function r(t) = a + t(b — a), where...Ch. 6.3 - True or False? Vector field F(x, y,z) = (y sinz)i...Ch. 6.3 - True or False?Vector field F(x,y,z)= yi + (x + z)j...Ch. 6.3 - Justify the Fundamental Theorem of Line Integrals...Ch. 6.3 - [T] Find cF.dr,,] where...Ch. 6.3 - [T] Evaluate line integral cF.dr, where...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - [T] Let F(x, y, z) = x2i + zsin(yz)j + y sin(yz)k....Ch. 6.3 - [T] Find line integral cF.dr,of vector field F(x,...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - Find the circulation and flux of field F=yi+xj...Ch. 6.3 - Compute ccosxcosydxsinxsinydy, where...Ch. 6.3 - Complete the proof of The Path Independence Test...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - easuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - ]Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - Find the counterclockwise circulation of field...Ch. 6.4 - Evaluate cy3dxx3y2dy,where C is the positively...Ch. 6.4 - Evaluate cy3dxx3dy,where C includes the two...Ch. 6.4 - Calculate cx2ydx+xy2dy,where C isa circle of...Ch. 6.4 - Calculate integral...Ch. 6.4 - Evaluate integral c( x 2+ y 2)dx+2xydy,where C is...Ch. 6.4 - Evaluate line integralc(ysin( y)cos( y)dx+2x sin...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - [T] Evaluate Green’s theorem using a computer...Ch. 6.4 - Evaluate c(x2y2xy+y2)ds,where C is the boundary of...Ch. 6.4 - Evaluate ( y+2)dx+( x1)dyc ( x1 ) 2+ ( y+2 )...Ch. 6.4 - 173. Evaluate xdx+ydy c x 2 + y 2 , . where C is...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - A particle starts at point (-2, 0), moves along...Ch. 6.4 - David and Sandra are skating on a frictionless...Ch. 6.4 - Use Green’s theorem to find the work done by force...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Evaluate line integral c y 2dx+x2dy,where C is...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c1+...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c(3y...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be a tiiangulai closed curve from (0, 0) to...Ch. 6.4 - Use Green’s theoiem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate cxydx+ x 3 y 3dy,...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let F(x,y)=(cos(x5))13y3i+13x3j.Find the...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be the boundary of square 0x,0y, traversed...Ch. 6.4 - Use Green’s theorem to evaluate line integral,...Ch. 6.4 - Use Green’s Theorem to evaluate integial...Ch. 6.4 - Use Green’s theorem in a plane to evaluate line...Ch. 6.4 - Calculate the outward flux of F = -xi + 2yj over a...Ch. 6.4 - 200. [T] Let C be circle x2+ y2= 4 oriented in the...Ch. 6.4 - Find the flux of field F = -xi + yj across x2+ y2...Ch. 6.4 - Let F = (y2— x2)i + (x2+y2)j, and let C be a...Ch. 6.4 - [T] Let C be unit circle x2+ y2 = 1 traversed once...Ch. 6.4 - [T] Find the outward flux of vector field F = xy2i...Ch. 6.4 - Consider region R bounded by parabolas y= x2and x...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - 233.w(x,y,z)=(x2+y2+z2)1/2Ch. 6.5 - 232.u(x,y,z)=ex(cosysiny)...Ch. 6.5 - 234.IfF(x,y,z)=2i+2xj+3ykCh. 6.5 - ...Ch. 6.5 - Find div F, given that F = f, where f(x,y,z)=xy3z2...Ch. 6.5 - 237. Find the divergence of F for vector field...Ch. 6.5 - Find the divergence of F for vector field...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r| and r =...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - Consider rotational velocity field v=0,10z,-10y....Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - wFor the following exercises, determine whether...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - wFor the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - wFor the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A paper cup has the shape of an inverted right...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - `For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - Draw the following vector fields. 431....Ch. 6 - Draw the following vector fields. 432....Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Evaluate the following integrals. 437....Ch. 6 - Evaluate the following integrals. 438. Cydx+xy2dy...Ch. 6 - Evaluate the following integrals. 439. Sxy2dS ,...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 444....Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 445....Ch. 6 - Use the divergence theorem to evaluate SFdS . 446....Ch. 6 - Use the divergence theorem to evaluate SFdS . 447....Ch. 6 - Find the amount of work perfumed by a 50 -kg woman...Ch. 6 - Find the total mass of a thin wire in the shape of...Ch. 6 - Find the total mass of a thin sheet in the shape...Ch. 6 - Use the divergence theorem to compute the value of...

Additional Math Textbook Solutions

Find more solutions based on key concepts
TRY IT YOURSELF 1 Find the mean of the points scored by the 51 winning teams listed on page 39.

Elementary Statistics: Picturing the World (7th Edition)

Evaluate the integrals in Exercises 1–14. 9.

University Calculus: Early Transcendentals (4th Edition)

A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How many choices a...

A First Course in Probability (10th Edition)

Mathematical Connections Explain why 25 cents is one-fourth of a dollar, yet 15 minutes is one-fourth of an hou...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

CHECK POINT 1 Write a word description of the set L = {a, b, c, d, e, f}.

Thinking Mathematically (6th Edition)

Version 2 of the Chain Rule Use Version 2 of the Chain Rule to calculate the derivatives of the following funct...

Calculus: Early Transcendentals (2nd Edition)

Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Text book image
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Text book image
Calculus Volume 1
Math
ISBN:9781938168024
Author:Strang, Gilbert
Publisher:OpenStax College
Text book image
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Text book image
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.; Author: Math and Science;https://www.youtube.com/watch?v=BHRWArTFgTs;License: Standard YouTube License, CC-BY