Chapter 6.1, Problem 6.39P

The truss shown consists of nine members and is support by a ball-and-socket at B, a short link at C, and two short links at D. (a) Check that this truss is a simple truss, that completely constrained, and that the reactions at its suppo are statically determinate. (b) Determine the force in each member for P = (−1200 N)j and Q = 0.

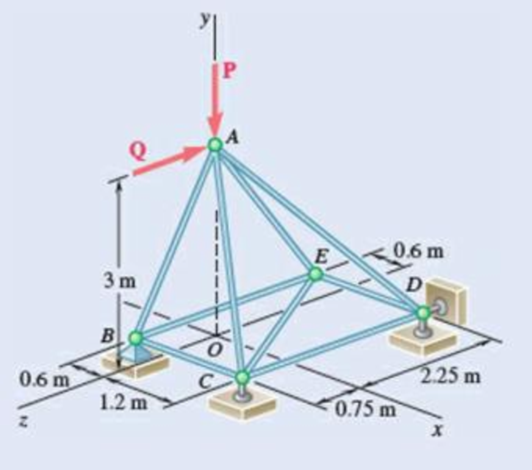
Fig. P6.39

To determine

Verify that the truss is a simple truss, completely constrained, and the reactions at the supports are statically determinate.

Answer to Problem 6.39P

The reactions at supports B, C, and D is $\underset{\_}{B=\left(800\text{N}\right)j;C=\left(100N\right)j;D=\left(300N\right)j}$.

Explanation of Solution

Given information:

The value of the force P is $\text{P}=\left(-1200\text{N}\right)j$.

The value of the force Q is zero.

Calculation:

Show the free-body diagram of the truss as in Figure 1.

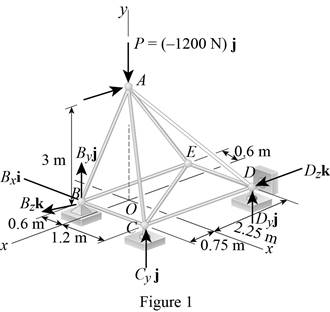
Find the vector coordinates by taking moment about point B.

$\begin{array}{l}{\displaystyle \sum {\text{M}}_B=0}\\ 1.8i\times C_{y}j+\left(1.8i-3k\right)\times \left(D_{y}j+D_{z}k\right)+\left(0.6i-0.75k\right)\times \left(-1200j\right)=0\\ 1.8C_{y}k+1.8D_{y}k-1.8D_{z}j-3D_{y}i-720k+900i=0\end{array}$

Equate the coefficients of i to zero.

$\begin{array}{l}3D_y-900=0\\ D_y=300\text{N}\\ D=\left(300N\right)j\end{array}$

Equate the coefficients of j to zero.

$D_z=0$

Equate the coefficients of k to zero.

$1.8C_y+1.8\left(D_y\right)-720=0$

Substitute 300 N for $D_y$.

$\begin{array}{l}1.8C_y+1.8\left(300\right)-720=0\\ 1.8C_y+540-720=0\\ C_y=100\text{N}\\ C=\left(100N\right)j\end{array}$

Resolve the force components in y-axis.

$\begin{array}{l}{\displaystyle \sum {\text{F}}_y=0}\\ B_{y}j+D_{y}j+C_{y}j-1200j=0\end{array}$

Substitute 300 N for $D_y$ and 100 N for $C_y$.

$\begin{array}{l}{B}_{y}j+300j+100j-1200j=0\\ B_y=800\text{N}\\ B=\left(800\text{N}\right)j\end{array}$

The unknown reactions can be calculated with the equilibrium equations. Therefore, the truss is statically determinate, completely constrained and simple truss.

Thus, the reactions at supports B, C, and D is $\underset{\_}{B=\left(800\text{N}\right)j;C=\left(100N\right)j;D=\left(300N\right)j}$.

To determine

Find the force in each member of the truss.

Answer to Problem 6.39P

The force in the member AB is $\underset{\_}{\text{840}\text{N}\left(\text{C}\right)}$.

The force in the member BC is $\underset{\_}{160\text{N}\left(\text{T}\right)}$.

The force in the member BE is $\underset{\_}{200\text{N}\left(\text{T}\right)}$.

The force in the member AC is $\underset{\_}{\text{110}\text{.6}\text{N}\left(\text{C}\right)}$.

The force in the member CE is $\underset{\_}{\text{233}\text{N}\left(\text{C}\right)}$.

The force in the member CD is $\underset{\_}{225\text{N}\left(\text{T}\right)}$.

The force in the member AD is $\underset{\_}{394\text{N}\left(\text{C}\right)}$.

The force in the member DE is $\underset{\_}{120\text{N}\left(\text{T}\right)}$.

The force in the member AE is $\underset{\_}{\text{zero}}$.

Explanation of Solution

Show the free-body diagram of the joint B as in Figure 2.

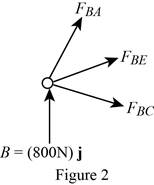
Resolve the force components as follows;

$\begin{array}{l}{\displaystyle \sum F=0};\\ F_{BA}+F_{BC}+F_{BE}+\left(800\text{N}\right)j=0\end{array}$

Write the vector value of $\overrightarrow{BA}$ as follows;

$\overrightarrow{BA}=0.6i+3j-0.75k$

Find the scalar quantity of BA using the relation.

$\begin{array}{c}BA=\sqrt{{0.6}^2+3^2+{\left(-0.75\right)}^2}\\ =3.15\text{m}\end{array}$

Find the force in the member AB as follows;

$F_{BA}=F_{AB}\frac{\overrightarrow{BA}}{BA}$

Substitute $\left(0.6i+3j-0.75k\right)$ for $\overrightarrow{BA}$ and 3.15 m for BA.

$\begin{array}{c}{F}_{BA}=F_{AB}\frac{\left(0.6i+3j-0.75k\right)}{3.15}\\ =F_{AB}\left(0.19048i+0.95238j-0.23810k\right)\end{array}$

Find the force in the member BC as follows;

$F_{BC}=F_{BC}i$

Find the force in the member BE as follows;

$F_{BE}=-F_{BE}k$

Equate the coefficients of j to zero.

$\begin{array}{c}0.95238F_{AB}+800=0\\ F_{AB}=-840\text{N}\\ \text{=840}\text{N}\left(\text{C}\right)\end{array}$

Equate the coefficients of i to zero.

$0.19048F_{AB}+F_{BC}=0$

Substitute –840 N for $F_{AB}$.

$\begin{array}{l}0.19048\left(-840\right)+F_{BC}=0\\ F_{BC}=160\text{N}\left(\text{T}\right)\end{array}$

Equate the coefficients of k to zero.

$\left(-0.23810\right)F_{AB}-F_{BE}=0$

Substitute –840 N for $F_{AB}$.

$\begin{array}{l}\left(-0.23810\right)\left(-840\right)-F_{BE}=0\\ F_{BE}=200\text{N}\left(\text{T}\right)\end{array}$

Therefore,

The force in the member AB is $\underset{\_}{\text{840}\text{N}\left(\text{C}\right)}$.

The force in the member BC is $\underset{\_}{160\text{N}\left(\text{T}\right)}$.

The force in the member BE is $\underset{\_}{200\text{N}\left(\text{T}\right)}$.

Show the free-body diagram of the joint C as in Figure 3.

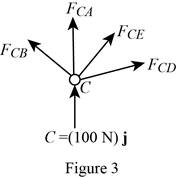
Resolve the force components as follows;

$\begin{array}{l}{\displaystyle \sum F=0};\\ F_{CA}+F_{CB}+F_{CD}+F_{CE}+\left(100\text{N}\right)j=0\end{array}$

Write the vector value of $\overrightarrow{CA}$ as follows;

$\overrightarrow{CA}=-1.20i+3j-0.75k$

Find the scalar quantity of CA using the relation.

$\begin{array}{c}CA=\sqrt{{\left(-1.20\right)}^2+3^2+{\left(-0.75\right)}^2}\\ =3.317\text{m}\end{array}$

Find the force in the member AC as follows;

$F_{CA}=F_{AC}\frac{\overrightarrow{CA}}{CA}$

Substitute $\left(-1.20i+3j-0.75k\right)$ for $\overrightarrow{CA}$ and 3.317 m for CA.

$\begin{array}{c}{F}_{CA}=F_{AC}\frac{\left(-1.20i+3j-0.75k\right)}{3.317}\\ =F_{AC}\left(0.36177i+0.90443j-0.22611k\right)\end{array}$

Find the force in the member CB as follows;

$F_{CB}=F_{BC}=-\left(160\text{N}\right)i$

Find the force in the member CD as follows;

$F_{CD}=-F_{CD}k$

Write the vector value of $\overrightarrow{CE}$ as follows;

$\overrightarrow{CE}=-1.80i-3k$

Find the scalar quantity of CE using the relation.

$\begin{array}{c}CE=\sqrt{{\left(-1.80\right)}^2+{\left(-3\right)}^2}\\ =3.499\text{m}\end{array}$

Find the force in the member CE as follows;

$F_{CE}=F_{CE}\frac{\overrightarrow{CE}}{CE}$

Substitute $\left(-1.80i-3k\right)$ for $\overrightarrow{CE}$ and 3.499 m for CE.

$\begin{array}{c}{F}_{CE}=F_{CE}\frac{\left(-1.80i-3k\right)}{3.499}\\ =F_{CE}\left(0.51443i-0.85739k\right)\end{array}$

Equate the coefficients of j to zero.

$\begin{array}{c}0.90443F_{AC}+100=0\\ F_{AC}=-110.6\text{N}\\ =\text{110}\text{.6}\text{N}\left(\text{C}\right)\end{array}$

Equate the coefficients of i to zero.

$-0.36177F_{AC}-160-0.51443F_{CE}=0$

Substitute –110.6 N for $F_{AC}$.

$\begin{array}{c}-0.36177\left(-110.6\right)-160-0.51443F_{CE}=0\\ F_{CE}=-233\text{N}\\ =\text{233}\text{N}\left(\text{C}\right)\end{array}$

Equate the coefficients of k to zero.

$-0.22611F_{AC}-F_{CD}-0.85739F_{CE}=0$

Substitute –110.6 N for $F_{AC}$ and –233 N for $F_{CE}$.

$\begin{array}{l}-0.22611\left(-110.6\right)-F_{CD}-0.85739\left(-233\right)=0\\ F_{CD}=225\text{N}\left(\text{T}\right)\end{array}$

Therefore,

The force in the member AC is $\underset{\_}{\text{110}\text{.6}\text{N}\left(\text{C}\right)}$.

The force in the member CE is $\underset{\_}{\text{233}\text{N}\left(\text{C}\right)}$.

The force in the member CD is $\underset{\_}{225\text{N}\left(\text{T}\right)}$.

Show the free-body diagram of the joint D as in Figure 4.

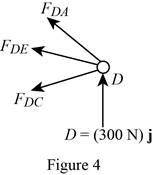
Resolve the force components as follows;

$\begin{array}{l}{\displaystyle \sum F=0};\\ F_{DA}+F_{DC}+F_{DE}+\left(300\text{N}\right)j=0\end{array}$

Write the vector value of $\overrightarrow{DA}$ as follows;

$\overrightarrow{DA}=-1.20i+3j+2.25k$

Find the scalar quantity of DA using the relation.

$\begin{array}{c}DA=\sqrt{{\left(-1.20\right)}^2+3^2+{2.25}^2}\\ =3.937\text{m}\end{array}$

Find the force in the member AD as follows;

$F_{DA}=F_{AD}\frac{\overrightarrow{DA}}{DA}$

Substitute $\left(-1.20i+3j+2.25k\right)$ for $\overrightarrow{DA}$ and 3.937 m for DA.

$\begin{array}{c}{F}_{DA}=F_{AD}\frac{\left(-1.20i+3j+2.25k\right)}{3.937}\\ =F_{AD}\left(-0.30480i+0.7620j-0.57150k\right)\end{array}$

Find the force in the member DC as follows;

$F_{DC}=F_{CD}k=\left(225\text{N}\right)k$

Find the force in the member DE as follows;

$F_{DE}=-F_{DE}i$

Equate the coefficients of j to zero.

$\begin{array}{c}0.7620F_{AD}+300=0\\ F_{AD}=-394\text{N}\\ =394\text{N}\left(\text{C}\right)\end{array}$

Equate the coefficients of i to zero.

$-0.30480F_{AD}-F_{DE}=0$

Substitute –394 N for $F_{AD}$.

$\begin{array}{l}-0.30480\left(-394\right)-F_{DE}=0\\ F_{DE}=120\text{N}\left(\text{T}\right)\end{array}$

Therefore,

The force in the member AD is $\underset{\_}{394\text{N}\left(\text{C}\right)}$.

The force in the member DE is $\underset{\_}{120\text{N}\left(\text{T}\right)}$.

Show the free-body diagram of the joint E as in figure 5.

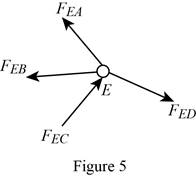
The member AE is not in the xz plane.

Therefore, the force in the member AE is $\underset{\_}{\text{zero}}$.