
(a)
(a)
Answer to Problem 98E
The events “diet B” and “Lose weight” are independent.
Explanation of Solution
Given information:
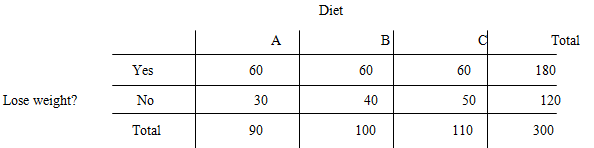
Two − way table comparing the effectiveness of three different diets (A, B, and C) on weight loss:

The two events are independent, if the probability of occurrence of one event does not affect the probability of occurrence of other event.
For the events “Diet B” and “Lose weight” to be independent,
The product of row total and column total, divided by the table total should be equal to the count in the table.
In the table, we can see that the count in row “Yes” and column “B” is already 60.
Thus,
The events “Diet B” and “Lose weight” are independent.
(b)
Fill the table such that no association exists between type of diet and whether a subject lost weight.
(b)
Answer to Problem 98E
Two − way table:

Explanation of Solution
Given information:
Two − way table comparing the effectiveness of three different diets (A, B, and C) on weight loss:

Two events are independent, when the probability of occurrence of one event does not affect the probability of occurrence of other event.
Then
The counts will be the product of the row total and the column total, divided by the table total provided in the bottom left corner of the table.
Calculate the counts in the two − way table:
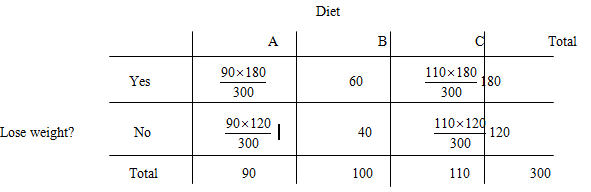
Thus,
The two – way table becomes:
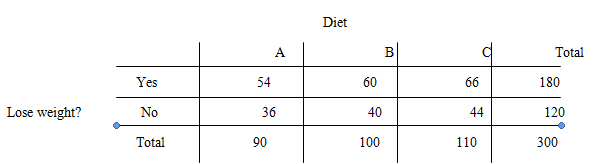
(c)
Fill the table such that an association exists between type of diet and whether a subject lost weight.
(c)
Answer to Problem 98E
Two − way table:
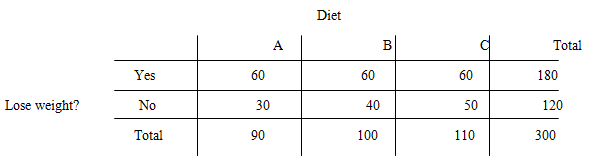
Explanation of Solution
Given information:
Two − way table comparing the effectiveness of three different diets (A, B, and C) on weight loss:
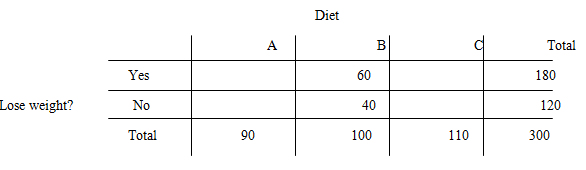
For two − way table, where an association exists between type of diet and whether a subject lost weight.
In this part, the count for column “A” and row “Yes” should be different from Part (b).
Suppose, if we choose the count 60 for column “A” and row “Yes” instead of 54 (in Part (b)).
Then
Put 60 in the column “A” and the row “Yes”.
And
Put the remaining counts according to the total counts of the rows and columns.
Thus,
The two − way table becomes:
Chapter 5 Solutions
PRACTICE OF STATISTICS F/AP EXAM
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Elementary Statistics (13th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Thinking Mathematically (6th Edition)
Introductory Statistics
College Algebra (7th Edition)
- Find the critical value for a left-tailed test using the F distribution with a 0.025, degrees of freedom in the numerator=12, and degrees of freedom in the denominator = 50. A portion of the table of critical values of the F-distribution is provided. Click the icon to view the partial table of critical values of the F-distribution. What is the critical value? (Round to two decimal places as needed.)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forwardShow all workarrow_forward
- Show all workarrow_forwardplease find the answers for the yellows boxes using the information and the picture belowarrow_forwardA marketing agency wants to determine whether different advertising platforms generate significantly different levels of customer engagement. The agency measures the average number of daily clicks on ads for three platforms: Social Media, Search Engines, and Email Campaigns. The agency collects data on daily clicks for each platform over a 10-day period and wants to test whether there is a statistically significant difference in the mean number of daily clicks among these platforms. Conduct ANOVA test. You can provide your answer by inserting a text box and the answer must include: also please provide a step by on getting the answers in excel Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value.arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





