Chapter 5, Problem 71E

a.

To determine

Draw the plots of the proportion of bird eggs hatching for the lowlands and mid-elevation areas versus exposure time.

Identify whether the shapes of the plots are as expected in case of “logistic” plots.

Answer to Problem 71E

The plot of the proportion of bird eggs hatching for the lowlands and mid-elevation areas versus exposure time is as follows:

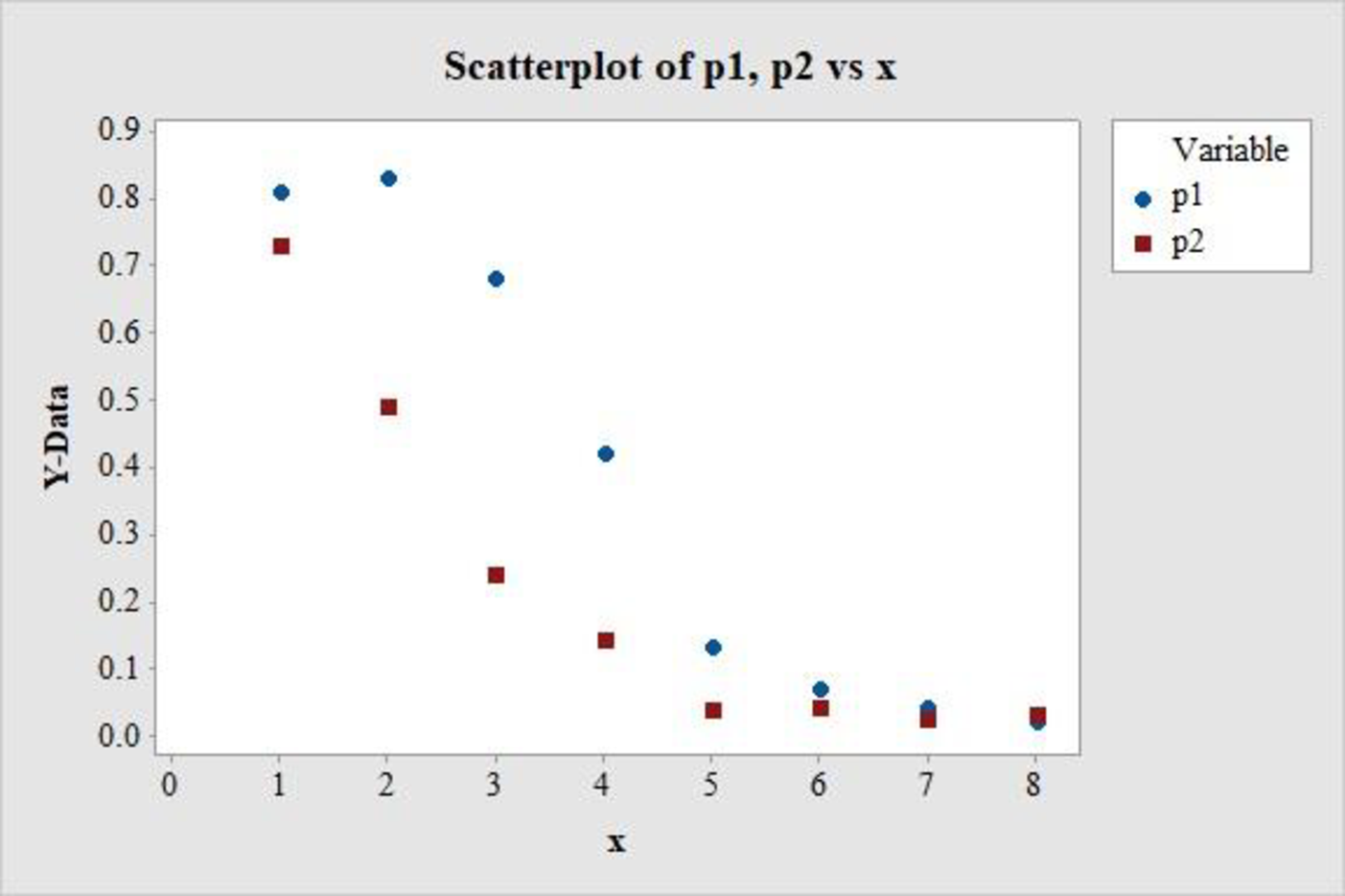
Explanation of Solution

Calculation:

The given data relates the proportion of bird eggs hatching for the lowlands, mid-elevation areas and cloud-forests with exposure time (days).

Denote the proportion of hatching for lowlands as $p_1$, that for mid elevation as $p_2$ and for cloud-forests as $p_3$. Denote the exposure time as x.

Scatterplot:

Software procedure:

Step-by-step procedure to draw the scatterplots using MINITAB software is given below:

• Choose Graph > Scatterplot.
• Choose Simple, and then click OK.
• Enter the column of p1 in the first cell under Y variables.
• Enter the column of x in the first cell under X variables.
• Enter the column of p2 in the second cell under Y variables.
• Enter the column of x in the second cell under X variables.
• Choose Multiple Graphs.
• Select Overlaid on the same graph under Show pairs of graph variables.
• Click OK in all dialogue boxes.

Thus, the scatterplot for the data is obtained.

The logistic plots usually have an approximate S-shaped distribution. In the above scatterplot, it is observed that both the proportions have approximately extended S-shaped distributions.

Hence, the shapes of the plots are more-or-less as expected in case of “logistic” plots.

b.

To determine

Find the value of $y^{\prime }=\ln \left(\frac{p}{1-p}\right)$ for each exposure time, in case of the cloud forest areas.

Fit a regression line of the form $y^{\prime }=a+b\left(\text{Exposure}\right)$.

Describe the significance of the negative slope.

Answer to Problem 71E

The regression line fitted to the given data is $\underset{\_}{y^{\prime }=1.513-0.5872x}$.

Explanation of Solution

Calculation:

Logistic regression:

The logistic regression equation for the prediction of a probability for the given value of the explanatory variable, x, is $\widehat{p}=\frac{e^{a+bx}}{1+e^{a+bx}}$, for constants a and b. For the logistic regression, $y^{\prime }=\ln \left(\frac{p}{1-p}\right)$ has a linear relationship with x, by the relation: $y^{\prime }=a+bx$.

The values of $y^{\prime }=\ln \left(\frac{p}{1-p}\right)$ can be obtained using software. Now, the proportion of hatching for cloud forest is $p_3$. In MINITAB, denote the column of $y^{\prime }$ as y*, so that $y*=\ln \left(\frac{p_3}{1-p_3}\right)$.

Data transformation $y*=\ln \left(\frac{p_3}{1-p_3}\right)$:

Software procedure:

Step-by-step procedure to transform the data using MINITAB software is given below:

• Choose Calc > Calculator.
• Enter the column of y* under Store result in variable.
• Enter the formula LN(‘p3’/(1–‘p3’)) under Expression.
• Click OK.

The transformed variable is stored in the column y*.

Data display:

Software procedure:

Step by step procedure to display the data using MINITAB software is given as,

• Choose Data > Display Data.
• Under Column, constants, and matrices to display, enter the column of y*.
• Click OK on all dialogue boxes.

The output using MINITAB software is given as follows:

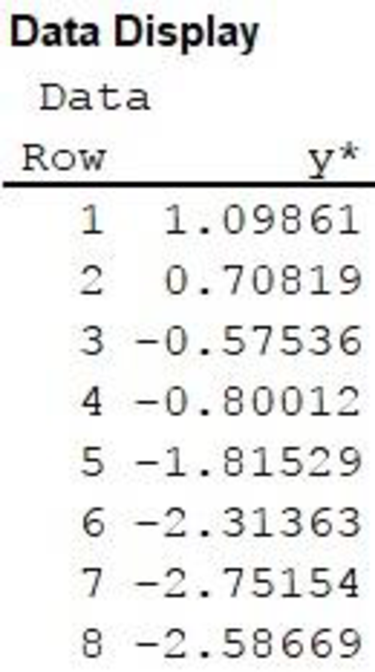
Regression equation:

Software procedure:

Step by step procedure to obtain the regression equation using the MINITAB software:

• Choose Stat > Regression > Regression > Fit Regression Model.
• Enter the column of y* under Responses.
• Enter the columns of x under Continuous predictors.
• Choose Results and select Analysis of Variance, Model Summary, Coefficients, Regression Equation.
• Click OK in all dialogue boxes.

Output obtained using MINITAB is given below:

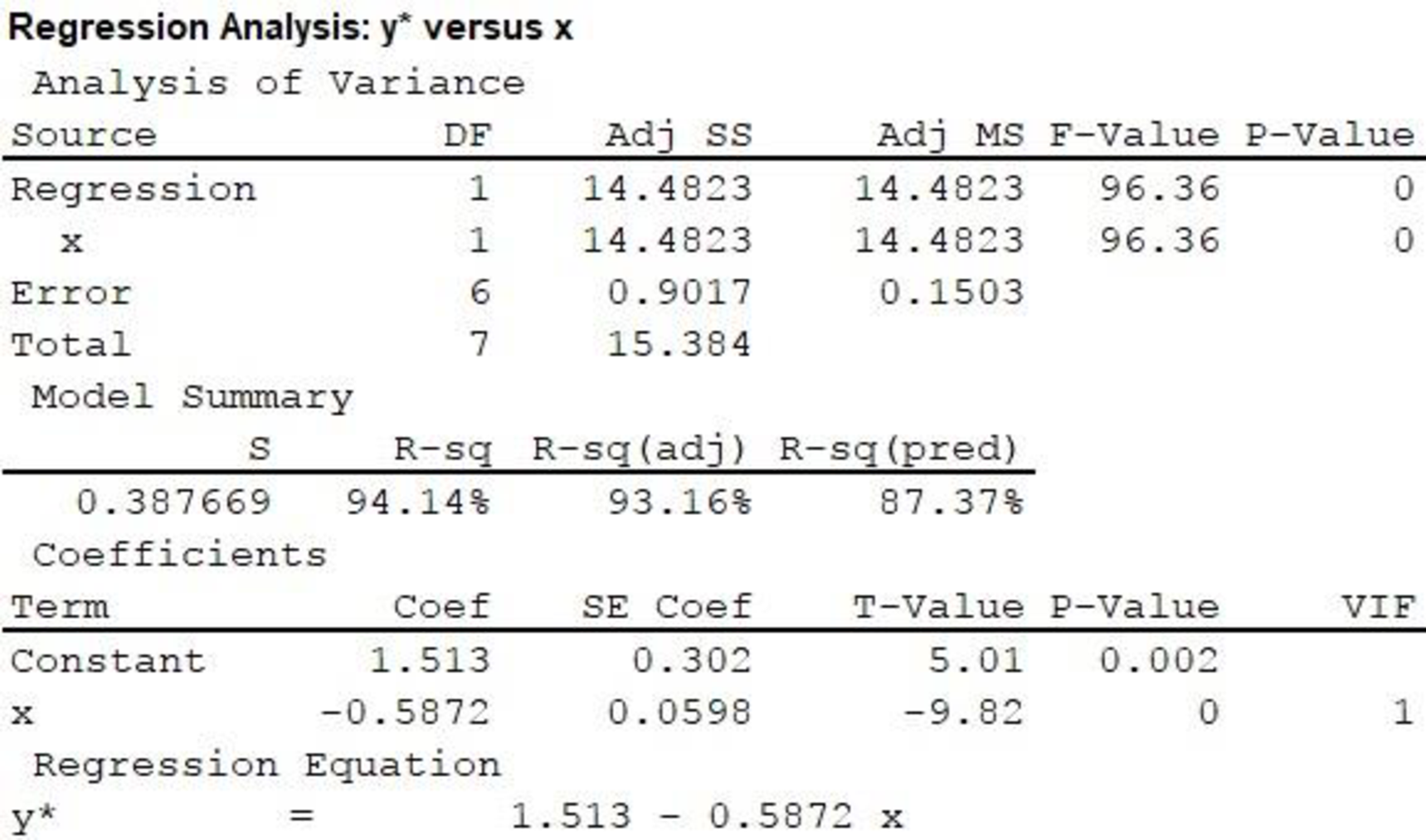
In the output, substituting $y*=y^{\prime }\left[=\ln \left(\frac{p_3}{1-p_3}\right)\right]$, the regression equation of the given form is $\underset{\_}{y^{\prime }=1.513-0.5872x}$.

It is observed that the slope of x is –0.5872, which is negative. A negative slope implies that an increase in x causes a decrease in yꞌ.

Now, it is known that the quantity $\frac{p_3}{1-p_3}$ is the odds of hatching in the cloud forest area, for a given exposure time and $y^{\prime }=\ln \left(\frac{p_3}{1-p_3}\right)$ is the natural logarithm of odds. Moreover, it is known that logarithm is an increasing function of the variable.

In this case, an increase in exposure time decreases the natural logarithm of odds of hatching in the cloud forest area, which, in turn, implies a decrease in the odds of hatching.

Thus, the negative slope implies that an increase in exposure time causes a decrease in the odds of hatching of an egg in the cloud forest area.

c.

To determine

Predict the proportion of hatching in the cloud forest conditions, for an exposure time of 3 days.

Predict the proportion of hatching in the cloud forest conditions, for an exposure time of 5 days.

Answer to Problem 71E

The proportion of hatching in the cloud forest conditions, for an exposure time of 3 days is 0.4382.

The proportion of hatching in the cloud forest conditions, for an exposure time of 5 days is 0.1942.

Explanation of Solution

Calculation:

For an exposure time of 3 days, substitute $x=3$ in the logistic equation:

$\begin{array}{c}{y}^{\prime }=1.513-0.5872x\\ \ln \left(\frac{{\widehat{p}}_3}{1-{\widehat{p}}_3}\right)=1.513-0.5872x\\ =1.513-\left(0.5872\times 3\right)\\ =1.513-1.7616\\ =-0.2486\end{array}$

Thus,

$\begin{array}{c}\frac{{\widehat{p}}_3}{1-{\widehat{p}}_3}=e^{-0.2486}\\ \approx \mathrm{0.7799.}\\ \frac{1-{\widehat{p}}_3}{{\widehat{p}}_3}=\frac{1}{0.7799}\\ \frac{1}{{\widehat{p}}_3}-1\approx 1.2822\end{array}$

    $\begin{array}{c}\frac{1}{{\widehat{p}}_3}=1+1.2822\\ =2.2822\\ {\widehat{p}}_3=\frac{1}{2.2822}\\ \approx \mathrm{0.4382.}\end{array}$

Thus, the proportion of hatching in the cloud forest conditions, for an exposure time of 3 days is 0.4382.

For an exposure time of 5 days, substitute $x=5$ in the logistic equation:

$\begin{array}{c}{y}^{\prime }=1.513-0.5872x\\ \ln \left(\frac{{\widehat{p}}_3}{1-{\widehat{p}}_3}\right)=1.513-0.5872x\\ =1.513-\left(0.5872\times 5\right)\\ =1.513-2.936\\ =-1.423\end{array}$

Thus,

$\begin{array}{c}\frac{{\widehat{p}}_3}{1-{\widehat{p}}_3}=e^{-1.423}\\ \approx \mathrm{0.241.}\\ \frac{1-{\widehat{p}}_3}{{\widehat{p}}_3}=\frac{1}{0.241}\\ \frac{1}{{\widehat{p}}_3}-1\approx 4.1496\end{array}$

    $\begin{array}{c}\frac{1}{{\widehat{p}}_3}=1+4.1496\\ =5.1496\\ {\widehat{p}}_3=\frac{1}{5.1496}\\ \approx \mathrm{0.1942.}\end{array}$

Thus, the proportion of hatching in the cloud forest conditions, for an exposure time of 5 days is 0.1942.

d.

To determine

Identify the point of exposure time, at which, the proportion of hatching in the cloud forest conditions changes from greater than 0.5 to less than 0.5.

Answer to Problem 71E

The exposure time, at which, the proportion of hatching in the cloud forest conditions changes from greater than 0.5 to less than 0.5 is 2.5766 days.

Explanation of Solution

Calculation:

For the proportion of hatching of 0.5, substitute ${\widehat{p}}_3=0.5$ in the logistic equation:

$\begin{array}{c}{y}^{\prime }=1.513-0.5872x\\ \ln \left(\frac{{\widehat{p}}_3}{1-{\widehat{p}}_3}\right)=1.513-0.5872x\\ \ln \left(\frac{0.5}{1-0.5}\right)=1.513-0.5872x\\ \ln \left(\frac{0.5}{0.5}\right)=1.513-0.5872x\\ \ln \left(1\right)=1.513-0.5872x\\ 0=1.513-0.5872x.\end{array}$

Thus,

$\begin{array}{c}0.5872x=1.513\\ x=\frac{1.513}{0.5872}\\ \approx \mathrm{2.5766.}\end{array}$

As a result, the exposure time for the proportion of hatching of 0.5 is 2.5766 days.

Now, from the explanation in Part b, an increase in the exposure time causes a decrease in the odds of hatching in the cloud forest conditions. Thus, an increase in exposure time from 2.5766 days would cause a decrease in the proportion of hatching, whereas a decrease in exposure time from 2.5766 days would cause an increase in the proportion of hatching.

Thus, the exposure time, at which, the proportion of hatching in the cloud forest conditions changes from greater than 0.5 to less than 0.5 is 2.5766 days.