Fox and McDonald's Introduction to Fluid Mechanics
9th Edition
ISBN: 9781118912652
Author: Philip J. Pritchard, John W. Mitchell
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5, Problem 66P
Consider a steady, laminar, fully developed, incompressible flow between two infinite plates, as shown. The flow is due to the motion of the left plate as well a pressure gradient that is applied in the y direction. Given the conditions that
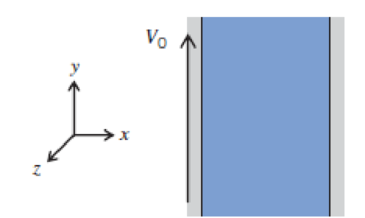
P5.66
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
5.73 Assume the liquid film in Example 5.9 is horizontal (i.e.,
0 = 0°) and that the flow is driven by a constant shear stress
on the top surface (y= h), Tyx= C. Assume that the liquid
film is thin enough and flat and that the flow is fully devel-
oped with zero net flow rate (flow rate Q= 0). Determine the
velocity profile u(y) and the pressure gradient dp/dx.
h = 1 mm
0 = 15°
Width b = 1 m
A VISCOUS FLUID FLOWS BETWEEN TWO PARALLEL AND INFINITELY LARGE PLATES KEPT AT A DISTANCE 2H FROM EACH OTHER. THE UPPER PLATE IS AT Y = H AND THE LOWE...
A viscous fluid flows between two parallel and infinitely large plates kept at a distance 2h from each other. The upper plate is at y = h and the lower plate is at y = - h. The considered
fluid flows mono directionally along the x-direction under a constant pressure gradient K = -dP/dx. The transverse profile of velocity is given by :
U(y) = K (h² - y²)
U (y) = (h-y)
U(y) = (h² - y²)
U(y) = (y²)
U(y) = K (h-y)
2h
EU(y)
5. A linear velocity profile is formed in a fluid between two plates as shown in the figure when
one of the plates is moved parallel to the other and there is no externally imposed pressure
gradient (i.e. there is no pump). If the top plate is travels at U = 0.3 m/s and the bottom
plate is held fixed and the two plates are separated by a distance d = 0.3 m/s, derive an
equation for the velocity profile u(y). Assume that the fluid in contact with either plate
moves at the same speed as the plate (this is called the no-slip condition).
U=0.3 m/s
d=0.3 m
Chapter 5 Solutions
Fox and McDonald's Introduction to Fluid Mechanics
Ch. 5 - Which of the following sets of equations represent...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - In an incompressible three-dimensional flow field,...Ch. 5 - In a two-dimensional incompressible flow field,...Ch. 5 - The three components of velocity in a velocity...Ch. 5 - The x component of velocity in a steady,...Ch. 5 - The y component of velocity in a steady...Ch. 5 - The velocity components for an incompressible...Ch. 5 - The radial component of velocity in an...Ch. 5 - A crude approximation for the x component of...
Ch. 5 - A useful approximation for the x component of...Ch. 5 - A useful approximation for the x component of...Ch. 5 - For a flow in the xy plane, the x component of...Ch. 5 - Consider a water stream from a jet of an...Ch. 5 - Which of the following sets of equations represent...Ch. 5 - For an incompressible flow in the r plane, the r...Ch. 5 - A viscous liquid is sheared between two parallel...Ch. 5 - A velocity field in cylindrical coordinates is...Ch. 5 - Determine the family of stream functions that...Ch. 5 - The stream function for a certain incompressible...Ch. 5 - Determine the stream functions for the following...Ch. 5 - Determine the stream function for the steady...Ch. 5 - Prob. 23PCh. 5 - A parabolic velocity profile was used to model...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - A flow field is characterized by the stream...Ch. 5 - Prob. 27PCh. 5 - A flow field is characterized by the stream...Ch. 5 - In a parallel one-dimensional flow in the positive...Ch. 5 - Consider the flow field given by V=xy2i13y3j+xyk....Ch. 5 - Prob. 31PCh. 5 - The velocity field within a laminar boundary layer...Ch. 5 - A velocity field is given by V=10ti10t3j. Show...Ch. 5 - The y component of velocity in a two-dimensional,...Ch. 5 - A 4 m diameter tank is filled with water and then...Ch. 5 - An incompressible liquid with negligible viscosity...Ch. 5 - Sketch the following flow fields and derive...Ch. 5 - Consider the low-speed flow of air between...Ch. 5 - As part of a pollution study, a model...Ch. 5 - As an aircraft flies through a cold front, an...Ch. 5 - Wave flow of an incompressible fluid into a solid...Ch. 5 - A steady, two-dimensional velocity field is given...Ch. 5 - A velocity field is represented by the expression...Ch. 5 - A parabolic approximate velocity profile was used...Ch. 5 - A cubic approximate velocity profile was used in...Ch. 5 - The velocity field for steady inviscid flow from...Ch. 5 - Consider the incompressible flow of a fluid...Ch. 5 - Consider the one-dimensional, incompressible flow...Ch. 5 - Expand (V)V in cylindrical coordinates by direct...Ch. 5 - Determine the velocity potential for (a) a flow...Ch. 5 - Determine whether the following flow fields are...Ch. 5 - The velocity profile for steady flow between...Ch. 5 - Consider the velocity field for flow in a...Ch. 5 - Consider the two-dimensional flow field in which u...Ch. 5 - Consider a flow field represented by the stream...Ch. 5 - Fluid passes through the set of thin, closely...Ch. 5 - A two-dimensional flow field is characterized as u...Ch. 5 - A flow field is represented by the stream function...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the flow field represented by the stream...Ch. 5 - Consider the velocity field given by V=Ax2i+Bxyj,...Ch. 5 - Consider again the viscometric flow of Example...Ch. 5 - The velocity field near the core of a tornado can...Ch. 5 - A velocity field is given by V=2i4xjm/s. Determine...Ch. 5 - Consider the pressure-driven flow between...Ch. 5 - Consider a steady, laminar, fully developed,...Ch. 5 - Assume the liquid film in Example 5.9 is not...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - Consider a steady, laminar, fully developed...Ch. 5 - A linear velocity profile was used to model flow...Ch. 5 - A cylinder of radius ri rotates at a speed ...Ch. 5 - The velocity profile for fully developed laminar...Ch. 5 - Assume the liquid film in Example 5.9 is...Ch. 5 - The common thermal polymerase chain reaction (PCR)...Ch. 5 - A tank contains water (20C) at an initial depth y0...Ch. 5 - For a small spherical particle of styrofoam...Ch. 5 - Use Excel to generate the progression to an...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Consider steady, incompressible, laminar flow of a Newtonian fluid in an infinitely long round pipe of diameter D or radius R = D/2. We ignore the effects of gravity. A constant pressure gradient ∂P/∂x is applied in the x-direction, where x1 and x2 are two arbitrary locations along the x-axis, and P1 and P2 are the pressures at those two locations. Note that we adopt a modified cylindrical coordinate system here with x instead of z for the axial component, namely, (r, ?, x) and (ur, u?, u). Derive an expression for the velocity field inside the pipe and estimate the viscous shear force per unit surface area acting on the pipe wall.arrow_forward4.62 (WILEYO Water flows through a duct of square cross section as shown in Fig. P4.62 with a constant, uniform velocity of V = 20 m/s. Consider fluid particles that lie along line A-B at time t = 0. Determine the position of these particles, denoted by line A'-B', when t = 0.20 s. Use the volume of fluid in the region be- tween lines A-B and A'-B' to determine the flowrate in the duct. Repeat the problem for fluid particles originally along line C-D; along line E-F. Compare your three answers. B' V = 20 m/s 0.5 m 60° A A' C E I Figure P4.62arrow_forward4. Q4) Derive an equation dr For axial viscous flow for axial flow along a circular pipe, where v is the velocity at radius r u is the viscosity of the fluid, and dp/dx is the pressure gradient along the pipe Hence show, by integrating the above expression, that is viscous flow takes place in the annular space between tow concentric pipes of radius R, and R2 (R,arrow_forwardTwo branches of water pipe merge to form a larger diameter as shown figure below. At a location at the junction (before completely merging) the nonuniform profile is observed at the depth of 6 ftDetermine the value of V (ft / s) .arrow_forward3. A circular cylinder of radius a is fitted with two pressure sensors to measure pressure at 0 = 180° and at 150°. The intent is to use this cylinder as a stream velocimeter, i.e. a device to determine the velocity of a stream by measuring the pressures at the two taps. The fluid is incompressible with a density of p. Figure for Part (a) U Figure for Part (b) 30 a) Using potential flow approximation, derive a formula for calculating U from the measured pressure difference at the two pressure taps. Note that for accurate measurement, the velocimeter must be aligned to have one of the taps exactly facing the stream as shown in the figure. (Ans: 2|Aptaps|/p ) b) Suppose the velocimeter has been misaligned by ổ degrees so that the two pressure taps are now at 180° + 8 and 150° + 8. Derive an expression for the percent error in stream velocity measurement. Then, calculate the error for 8 = 5°,10° and –10°. (Ans: [2/(sin2(150 + 8) – sin²(180 + 8) )– 1] × 100 )arrow_forward5.69 Consider a steady, laminar, fully developed incompressible flow between two infinite parallel plates separated by a distance 2h as shown below. The top plate moves with a velocity Vo. Derive an expression for the velocity profile. Determine the pressure gradient for which the flow rate is zero. Plot the profile for that condition. Vo y 2 harrow_forwardA two dimensional, steady, incompressible and potential flow field of water (ρ=1000 kg/m3) is given with velocity components u and v. If the velocity component, u is given as u=1,5xy m/s with the magnitude of maximum pressure in the field as 42156 Pa. a) At x=+1 m and y=+2 m point, what is the magnitude of the velocity component v (in m/s)? (Please use 2 decimal digits in your answer) b) At x=+1 m and y=+2 m point, what is the magnitude of dynamic pressure (in Pa)? (Please do not use any decimal digit in your answer) c) At x=+1 m and y=+2 m point, what is the magnitude of static pressure (in Pa)? (Please do not use any decimal digit in your answer)arrow_forward4.5 The water flows in a 4m wide canal at a velocity of 5 m/s. A wedge-shaped column bifurcates the stream, as shown in Fig. 4.29. Calculate the force per unit depth exerted by the water stream on the column, if the wedge angle (a) is 30°. V=5m/s V=5 m/s V=5 m/s Fig. 4.29 [Ans: 3407.4N]arrow_forwardYou are given the velocity profile within a thin layer of liquid, draining from an inclined plane as vx = v0 (ay/h − y2/h2), where v0 is the surface velocity and a is a constant that needs to be determined. The height of the liquid film h = 2 cm and the flow rate is 1.8liters/minute. The plane has width 10 cm into the paper.(i). Determine the constant a by applying a suitable boundary condition at y = h.arrow_forward4. Show that v= 3xi+ (t- 6xy)j is a possible fluid velocity for two-dimensional unsteady flow of a homogeneous incompressible fluid. Hence, find the pressure p(x, y,t) at any point of the fluid using Euler's equation of motion given that the body force per unit mass is F = 6 yi+18x yj.arrow_forward6.41 The velocity potential for a certain inviscid, incompressible flow field is given by the equation o = 2x?y – G) where o has the units of m/s when x and y are in meters. Deter- mine the pressure at the point x = 2 m, y = 2 m if the pressure at x = 1 m, y = 1 m is 200 kPa. Elevation changes can be neglected, and the fluid is water.arrow_forwardQ.5 The velocity components in x and y direction 2 are given by u = Axy° - xy; v = > ху; v — ху = xy² – 3/4 .4 y*. The value of A for a possible flow field involving an incompressible fluid is: A -3/4 В 3 C 4/3 D -4/3arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Introduction to Kinematics; Author: LearnChemE;https://www.youtube.com/watch?v=bV0XPz-mg2s;License: Standard youtube license