Chapter 5, Problem 59RE

Spreading of a Disease Jack and Diane live in a small town of 50 people. Unfortunately, both Jack and Diane have a cold. Those who come in contact with someone who has this cold will themselves catch the cold. The following data represent the number of people in the small town who have caught the cold after t days.

(a) Using a graphing utility, draw a scatter diagram of the data. Comment on the type of relation that appears to exist between the days and number of people with a cold.

(b) Using a graphing utility, build a logistic model from the data.

(c) Graph the function found in part (b) on the scatter diagram.

(d) According to the function found in part (b). what is the maximum number of people who will catch the cold? In reality', what is the maximum number of people who could catch the cold?

(e) Sometime between the second and third day, 10 people in the town had a cold. According to the model found in part (b). when did 10 people have a cold?

(f) How long will it take for 46 people to catch the cold?

To determine

To find:

a. Using graphing utility, draw a scatter diagram of the data. Comment on the type of relation that appears to exist between the days and number of people with a cold.

Answer to Problem 59RE

a.

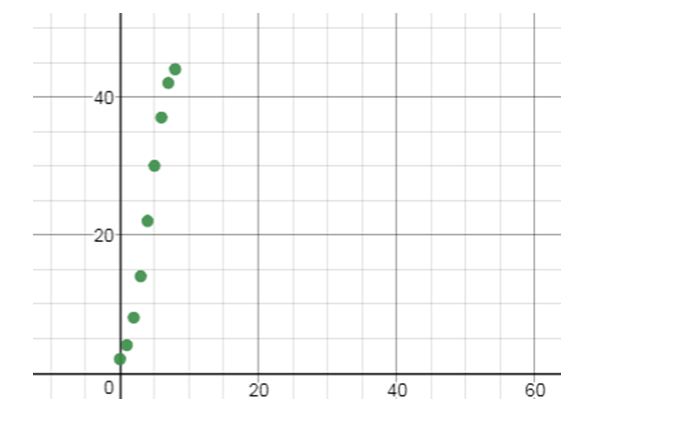
Explanation of Solution

Given:

The logistic model.

Calculation:

a. Graph:

To determine

To find:

b. Using a graphing utility, build a logistic model from the data.

Answer to Problem 59RE

b. $C=\frac{46.9292}{1+21.2733e^{-0.7306t}}$

Explanation of Solution

Given:

The logistic model.

Calculation:

b. $C=\frac{46.9292}{1+21.2733e^{-0.7306t}}$

To determine

To find:

c. Graph the function found in part (b) on the scatter diagram.

Answer to Problem 59RE

c.

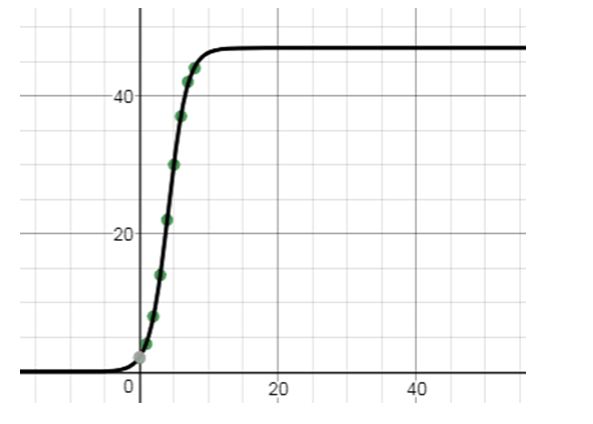
Explanation of Solution

Given:

The logistic model.

Calculation:

c. Scatter diagram.

To determine

To find:

d. According to the function found in part(b), what is the maximum number of people who will catch the cold? In reality, what is the maximum number of people who could catch the cold?

Answer to Problem 59RE

d. $47,\text{ 50}$

Explanation of Solution

Given:

The logistic model.

Calculation:

d. $C=\frac{46.9292}{1+21.2733e^{-0.7306t}}$

$C=\frac{46.9292}{1+21.2733e^{-0.7306\left(\infty \right)}}\approx 47$, the maximum number of people is 50.

To determine

To find:

e. Sometime between the second and third day, 10 people in the town had a cold. According to the model found in part(b), when did 10 people have a cold?

Answer to Problem 59RE

e. $2.4$

Explanation of Solution

Given:

The logistic model.

Calculation:

e. $10=\frac{46.9292}{1+21.2733e^{-0.7306\left(t\right)}}$

$10\left(1+21.2733e^{-0.7306\left(t\right)}\right)=46.992$

$10\left(21.2733\right)e^{-0.7306\left(t\right)}=36.992$

$-0.7306t=-1.7510$

$t=2.4$ days, during the tenth hour of day.

To determine

To find:

f. How long will it take for 46 people to catch the cold?

Answer to Problem 59RE

f. $9.5$

Explanation of Solution

Given:

The logistic model.

Calculation:

f. $46=\frac{46.9292}{1+21.2733e^{-0.7306\left(t\right)}}$

$46\left(1+21.2733e^{-0.7306\left(t\right)}\right)=46.9292$

$-0.7306t=-6.9595$

$t=9.5$ days.