Chapter 5, Problem 56RE

Logistic Growth The logistic growth model $Pt\text{ = }\frac{0.8}{1\text{ + 1}\text{.67}{e}^{-0.16t}}$ represents the proportion of new cars with a global positioning system (GPS). Let $t=0$ represent 2006, $t=1$ represent 2007, and so on.

(a) What proportion of new cars in 2006 had a GPS?

(b) Determine the maximum proportion of new cars that have a GPS.

c) Using a graphing utility, graph $P=P\left(t\right)$.

(d) When will $75\%$ of new cars have a GPS?

To determine

To find:

a. What proportion of new cars in 2006 had a GPS?

Answer to Problem 56RE

a. $0.3$

Explanation of Solution

Given:

$P\left(t\right)=\frac{0.8}{1+1.67e^{-0.16t}}$

Calculation:

a. $P\left(t\right)=\frac{0.8}{1+1.67e^{-0.16t}}$

$P\left(0\right)=\frac{0.8}{1+1.67e^{-0.16\left(0\right)}}\approx 0.3$

To determine

To find:

b. Determine the maximum proportion of new cars that have a GPS.

Answer to Problem 56RE

b. $0.8$

Explanation of Solution

Given:

$P\left(t\right)=\frac{0.8}{1+1.67e^{-0.16t}}$

Calculation:

b. $P\left(t\right)=\frac{0.8}{1+1.67e^{-0.16t}}$

$\underset{t\to \infty }{\lim }\frac{0.8}{1+1.67e^{-0.16t}}=0.8$

To determine

To find:

c. Using a graphing utility, graph $P=P\left(t\right)$.

Answer to Problem 56RE

c.

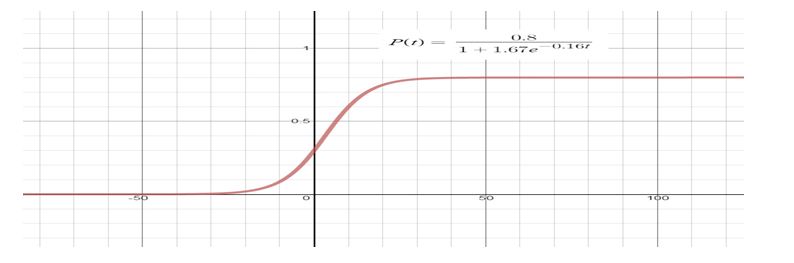
Explanation of Solution

Given:

$P\left(t\right)=\frac{0.8}{1+1.67e^{-0.16t}}$

Calculation:

c. Graph:

To determine

To find:

d. When will $75\%$ of new cars have a GPS?

Answer to Problem 56RE

d. In 2026

Explanation of Solution

Given:

$P\left(t\right)=\frac{0.8}{1+1.67e^{-0.16t}}$

Calculation:

d. $P\left(t\right)=\frac{0.8}{1+1.67e^{-0.16t}}$

$0.75=\frac{0.8}{1+1.67e^{-0.16t}}=20.13$

Therefore, 2026.