Chapter 5, Problem 12CT

(a)

To determine

The domain of $f$ , where $f\left(x\right)=4^{x+1}-2$ .

Answer to Problem 12CT

Solution:

The domain of the function $f\left(x\right)=4^{x+1}-2$ is $\left(-\infty ,\infty \right)$ .

Explanation of Solution

Given information:

The function is $f\left(x\right)=4^{x+1}-2$ .

Consider the function $f\left(x\right)=4^{x+1}-2$ .

The given function can be written as $f\left(x\right)=4\cdot 4^x-2$ .

The given function is exponential function.

The domain of the exponential function is $\left(-\infty ,\infty \right)$ .

Thus, the domain of the function $f\left(x\right)=4^{x+1}-2$ is $\left(-\infty ,\infty \right)$ .

(b)

To determine

To graph: The function $f\left(x\right)=4^{x+1}-2$ .

Explanation of Solution

Given information:

The function is $f\left(x\right)=4^{x+1}-2$ .

Graph:

Use the steps below to graph the function using graphing calculator:

Step I: Press the ON key.

Step II: Now, press [Y=]. Input the right hand side of the function $y=4^{x+1}-2$ in $Y_1$ .

Step III: Then hit [Graph] key to view the graph.

The graph of the function $f\left(x\right)=4^{x+1}-2$ is as follows:

  

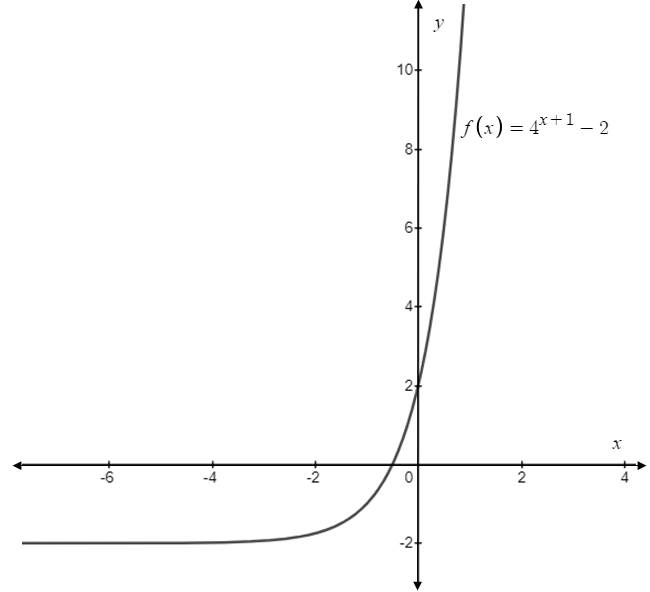
Interpretation:

By looking at the graph, it is observed that as $x\to -\infty$ , $y$ tends to $-2$ . The above graph shows that graph of the function $f\left(x\right)=4^{x+1}-2$ .

(c)

To determine

The range of any asymptotes from the graph of $f$ , where $f\left(x\right)=4^{x+1}-2$ .

Answer to Problem 12CT

Solution:

1) The range of the function $f\left(x\right)=4^{x+1}-2$ is $\left(-2,\infty \right)$ .

2) The horizontal asymptote of $f\left(x\right)=4^{x+1}-2$ is $y=-2$ .

Explanation of Solution

Given information:

The function is $f\left(x\right)=4^{x+1}-2$ .

The domain of the function $f\left(x\right)=4^{x+1}-2$ is $\left(-\infty ,\infty \right)$ .

Range of the function is the set of values of the dependent variable for which a function is defined.

From the graph, range of $f\left(x\right)=4^{x+1}-2$ is $\left(-2,\infty \right)$ .

As $x\to -\infty$ , $f(x)$ approaches to $-2$ .

Therefore, the horizontal asymptote of $f\left(x\right)=4^{x+1}-2$ is $y=-2$ .

(d)

To determine

The inverse of $f$ , where $f\left(x\right)=4^{x+1}-2$ .

Answer to Problem 12CT

Solution:

The inverse of $f\left(x\right)=4^{x+1}-2$ is $f^{-1}\left(x\right)=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$ .

Explanation of Solution

Given information:

The function is $f\left(x\right)=4^{x+1}-2$ .

Consider the function $f\left(x\right)=4^{x+1}-2$ .

Step 1: Replace $f\left(x\right)$ with $y$ ,

  $\Rightarrow y=4^{x+1}-2$

Step 2: Interchange the variables $x$ and $y$ .

Interchange the variables $x$ and $y$ in $y=4^{x+1}-2$ to obtain $x=4^{y+1}-2$ .

Step 3: Solve for $y$ to obtain explicit form of $f^{-1}$ .

Add $2$ on both sides,

  $\Rightarrow x+2=4^{y+1}$

Taking natural logarithm function from both sides of $x+2=4^{y+1}$ ,

  $\Rightarrow \ln \left(x+2\right)=\ln 4^{y+1}$

By using $\ln a^M=M\ln a$ ,

  $\Rightarrow \ln \left(x+2\right)=\left(y+1\right)\ln 4$

  $\Rightarrow \ln \left(x+2\right)=y\ln 4+\ln 4$

  $\Rightarrow \ln \left(x+2\right)-\ln 4=y\ln 4$

  $\Rightarrow y=\frac{\ln \left(x+2\right)-\ln 4}{\ln 4}$

By using $\ln \left(\frac{M}{N}\right)=\ln M-\ln N$ ,

  $\Rightarrow y=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$

Replace $y$ by $f^{-1}\left(x\right)$ ,

  $\Rightarrow f^{-1}\left(x\right)=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$

Therefore, the inverse of $f\left(x\right)=4^{x+1}-2$ is $f^{-1}\left(x\right)=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$ .

(e)

To determine

The domain and range of $f^{-1}$ .

Answer to Problem 12CT

Solution:

The domain of $f^{-1}\left(x\right)$ is $\left(-2,\infty \right)$ , and range of $f^{-1}\left(x\right)$ is $\left(-\infty ,\infty \right)$ .

Explanation of Solution

Given information:

The function is $f\left(x\right)=4^{x+1}-2$ .

From the part (d), $f^{-1}\left(x\right)=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$ .

  $f^{-1}$ is logarithm function.

The logarithm function is defined only for positive real numbers.

The domain of the function is the set of real numbers such that $\frac{x+2}{4}>0$ .

  $\Rightarrow x+2>0$

  $\Rightarrow x>-2$

The domain of $f^{-1}$ is $\left(-2,\infty \right)$ .

The domain of the function $f\left(x\right)=4^{x+1}-2$ is $\left(-\infty ,\infty \right)$ .

By using domain of $f\left(x\right)$ = range of $f^{-1}\left(x\right)$ ,

The range of $f^{-1}\left(x\right)$ is $\left(-\infty ,\infty \right)$ .

Therefore, the domain of $f^{-1}\left(x\right)$ is $\left(-2,\infty \right)$ , and range of $f^{-1}\left(x\right)$ is $\left(-\infty ,\infty \right)$ .

(e)

To determine

To graph: The function $f^{-1}$ .

Explanation of Solution

Given information:

The function is $f\left(x\right)=4^{x+1}-2$ .

Graph:

From the part (d), $f^{-1}\left(x\right)=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$ .

Use the steps below to graph the function using graphing calculator:

Step I: Press the ON key.

Step II: Now, press [Y=]. Input the right hand side of the function $y=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$ in $Y_1$ .

Step III: Then hit [Graph] key to view the graph.

By using the graphing calculator, the graph of the function $f^{-1}\left(x\right)=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$ is:

  

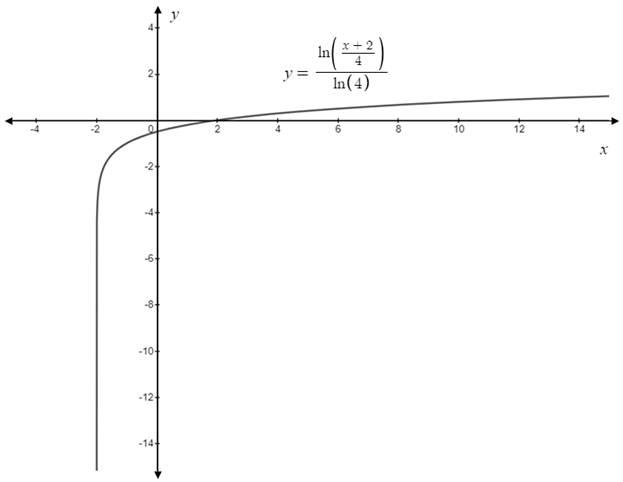
Interpretation:

By looking at the graph, it is observed that as $x\to -2$ , $y\to -\infty$ , and as $x$ value increases, $y$ value also increases. The above graph shows that graph of the function $f^{-1}\left(x\right)=\frac{\ln \left(\frac{x+2}{4}\right)}{\ln 4}$ .