Precalculus Enhanced with Graphing Utilities
6th Edition
ISBN: 9780321795465
Author: Michael Sullivan, Michael III Sullivan
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.4, Problem 67AYU
In Problems 65-72, the graph of a logarithmic function is given. Match each graph to one of the following functions:
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
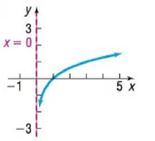
Expert Solution & Answer
To determine
To find: The graph of a logarithmic function .Match each graph to one of the following functions.
a.
b.
c.
d.
e.
f.
g.
h.
Answer to Problem 67AYU
a.
Explanation of Solution
Given:
The graph of a logarithmic function.
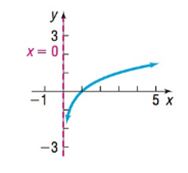
Calculation:
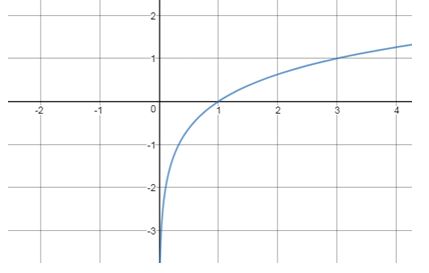
Therefore answer is a. .
Chapter 5 Solutions
Precalculus Enhanced with Graphing Utilities
Ch. 5.1 - Find f( 3 ) if f( x )=4 x 2 +5x . (pp. 60-62)Ch. 5.1 - Find f(3x) if f(x)=42 x 2 . (pp. 60-62)Ch. 5.1 - Find the domain of the function f(x)= x 2 1 x 2 25...Ch. 5.1 - Given two functions f and g , the _____, denoted...Ch. 5.1 - Prob. 5AYUCh. 5.1 - True or False The domain of the composite function...Ch. 5.1 - In Problems 9 and 10, evaluate each expression...Ch. 5.1 - In Problems 9 and 10, evaluate each expression...Ch. 5.1 - In Problems 11 and 12, evaluate each expression...Ch. 5.1 - In Problems 11 and 12, evaluate each expression...
Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - In Problems 13-22, for the given functions f and g...Ch. 5.1 - Prob. 21AYUCh. 5.1 - Prob. 22AYUCh. 5.1 - Prob. 23AYUCh. 5.1 - Prob. 24AYUCh. 5.1 - Prob. 25AYUCh. 5.1 - Prob. 26AYUCh. 5.1 - Prob. 27AYUCh. 5.1 - Prob. 28AYUCh. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 23-38, for the given functions f and g...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 39-46, show that (fg)( x )=(gf)( x )=x...Ch. 5.1 - In Problems 47-52, find functions f and g so that...Ch. 5.1 - In Problems 47-52, find functions f and g so that...Ch. 5.1 - In Problems 47-52, find functions f and g so that...Ch. 5.1 - In Problems 47-52, find functions f and g so that...Ch. 5.1 - In Problems 47-52, find functions f and g so that...Ch. 5.1 - In Problems 47-52, find functions f and g so that...Ch. 5.1 - Prob. 59AYUCh. 5.1 - Prob. 60AYUCh. 5.1 - Prob. 61AYUCh. 5.1 - Prob. 62AYUCh. 5.1 - Prob. 63AYUCh. 5.1 - Prob. 64AYUCh. 5.1 - Prob. 65AYUCh. 5.1 - Prob. 66AYUCh. 5.1 - Prob. 67AYUCh. 5.1 - Prob. 68AYUCh. 5.1 - Prob. 69AYUCh. 5.1 - Prob. 70AYUCh. 5.1 - Prob. 71AYUCh. 5.1 - Prob. 72AYUCh. 5.1 - Prob. 73AYUCh. 5.1 - Prob. 74AYUCh. 5.1 - Prob. 75AYUCh. 5.1 - Prob. 76AYUCh. 5.1 - Prob. 77AYUCh. 5.2 - Is the set of ordered pairs { ( 1,3 ),( 2,3 ),(...Ch. 5.2 - Where is the function f( x )= x 2 increasing?...Ch. 5.2 - What is the domain of f(x)= x+5 x 2 +3x18 ? (pp....Ch. 5.2 - Simplify: 1 x +1 1 x 2 1 (pp. A39-A41)Ch. 5.2 - If x 1 and x 2 are two different inputs of a...Ch. 5.2 - If every horizontal line intersects the graph of a...Ch. 5.2 - If f is a one-to-one function and f( 3 )=8 , then...Ch. 5.2 - If f 1 denotes the inverse of a function f , then...Ch. 5.2 - If the domain of a one-to-one function f is [ 4, )...Ch. 5.2 - True or False If f and g are inverse functions,...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 13-20, determine whether the function...Ch. 5.2 - In Problems 21-26, the graph of a function f is...Ch. 5.2 - In Problems 21-26, the graph of a function f is...Ch. 5.2 - In Problems 21-26, the graph of a function f is...Ch. 5.2 - In Problems 21-26, the graph of a function f is...Ch. 5.2 - In Problems 21-26, the graph of a function f is...Ch. 5.2 - In Problems 21-26, the graph of a function f is...Ch. 5.2 - Prob. 25AYUCh. 5.2 - Prob. 26AYUCh. 5.2 - Prob. 27AYUCh. 5.2 - Prob. 28AYUCh. 5.2 - Prob. 29AYUCh. 5.2 - Prob. 30AYUCh. 5.2 - Prob. 31AYUCh. 5.2 - Prob. 32AYUCh. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 35-44, verify that the functions f and...Ch. 5.2 - In Problems 45-50, the graph of a one-to-one...Ch. 5.2 - In Problems 45-50, the graph of a one-to-one...Ch. 5.2 - In Problems 45-50, the graph of a one-to-one...Ch. 5.2 - In Problems 45-50, the graph of a one-to-one...Ch. 5.2 - In Problems 45-50, the graph of a one-to-one...Ch. 5.2 - In Problems 45-50, the graph of a one-to-one...Ch. 5.2 - Prob. 49AYUCh. 5.2 - Prob. 50AYUCh. 5.2 - Prob. 51AYUCh. 5.2 - Prob. 52AYUCh. 5.2 - Prob. 53AYUCh. 5.2 - Prob. 54AYUCh. 5.2 - Prob. 55AYUCh. 5.2 - Prob. 56AYUCh. 5.2 - Prob. 57AYUCh. 5.2 - Prob. 58AYUCh. 5.2 - Prob. 59AYUCh. 5.2 - Prob. 60AYUCh. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - In Problems 63-74, the function f is one-to-one....Ch. 5.2 - Prob. 73AYUCh. 5.2 - Prob. 74AYUCh. 5.2 - Prob. 75AYUCh. 5.2 - Prob. 76AYUCh. 5.2 - Prob. 77AYUCh. 5.2 - Prob. 78AYUCh. 5.2 - Prob. 79AYUCh. 5.2 - Prob. 80AYUCh. 5.2 - Prob. 81AYUCh. 5.2 - Prob. 82AYUCh. 5.2 - Prob. 83AYUCh. 5.2 - Prob. 84AYUCh. 5.2 - Prob. 85AYUCh. 5.2 - Prob. 86AYUCh. 5.2 - Prob. 87AYUCh. 5.2 - Prob. 88AYUCh. 5.2 - Prob. 89AYUCh. 5.2 - Prob. 90AYUCh. 5.2 - Prob. 91AYUCh. 5.2 - Prob. 92AYUCh. 5.2 - Prob. 93AYUCh. 5.2 - Prob. 94AYUCh. 5.2 - Prob. 95AYUCh. 5.2 - Prob. 96AYUCh. 5.2 - Prob. 97AYUCh. 5.2 - Prob. 98AYUCh. 5.2 - Prob. 99AYUCh. 5.2 - Prob. 100AYUCh. 5.2 - Prob. 101AYUCh. 5.2 - Prob. 102AYUCh. 5.2 - Prob. 103AYUCh. 5.3 - Prob. 1AYUCh. 5.3 - Prob. 2AYUCh. 5.3 - Prob. 3AYUCh. 5.3 - Prob. 4AYUCh. 5.3 - Prob. 5AYUCh. 5.3 - Prob. 6AYUCh. 5.3 - Prob. 7AYUCh. 5.3 - Prob. 8AYUCh. 5.3 - Prob. 9AYUCh. 5.3 - Prob. 10AYUCh. 5.3 - Prob. 11AYUCh. 5.3 - Prob. 12AYUCh. 5.3 - Prob. 13AYUCh. 5.3 - Prob. 14AYUCh. 5.3 - Prob. 15AYUCh. 5.3 - Prob. 16AYUCh. 5.3 - Prob. 17AYUCh. 5.3 - Prob. 18AYUCh. 5.3 - Prob. 19AYUCh. 5.3 - Prob. 20AYUCh. 5.3 - Prob. 21AYUCh. 5.3 - Prob. 22AYUCh. 5.3 - Prob. 23AYUCh. 5.3 - Prob. 24AYUCh. 5.3 - Prob. 25AYUCh. 5.3 - Prob. 26AYUCh. 5.3 - Prob. 27AYUCh. 5.3 - Prob. 28AYUCh. 5.3 - Prob. 29AYUCh. 5.3 - Prob. 30AYUCh. 5.3 - Prob. 31AYUCh. 5.3 - Prob. 32AYUCh. 5.3 - Prob. 33AYUCh. 5.3 - Prob. 34AYUCh. 5.3 - Prob. 35AYUCh. 5.3 - Prob. 36AYUCh. 5.3 - Prob. 37AYUCh. 5.3 - Prob. 38AYUCh. 5.3 - Prob. 39AYUCh. 5.3 - Prob. 40AYUCh. 5.3 - Prob. 41AYUCh. 5.3 - Prob. 42AYUCh. 5.3 - Prob. 43AYUCh. 5.3 - Prob. 44AYUCh. 5.3 - Prob. 45AYUCh. 5.3 - Prob. 46AYUCh. 5.3 - Prob. 47AYUCh. 5.3 - Prob. 48AYUCh. 5.3 - Prob. 49AYUCh. 5.3 - Prob. 50AYUCh. 5.3 - Prob. 51AYUCh. 5.3 - Prob. 52AYUCh. 5.3 - Prob. 53AYUCh. 5.3 - Prob. 54AYUCh. 5.3 - Prob. 55AYUCh. 5.3 - Prob. 56AYUCh. 5.3 - Prob. 57AYUCh. 5.3 - Prob. 58AYUCh. 5.3 - Prob. 59AYUCh. 5.3 - Prob. 60AYUCh. 5.3 - Prob. 61AYUCh. 5.3 - Prob. 62AYUCh. 5.3 - Prob. 63AYUCh. 5.3 - Prob. 64AYUCh. 5.3 - Prob. 65AYUCh. 5.3 - Prob. 66AYUCh. 5.3 - Prob. 67AYUCh. 5.3 - Prob. 68AYUCh. 5.3 - Prob. 69AYUCh. 5.3 - Prob. 70AYUCh. 5.3 - Prob. 71AYUCh. 5.3 - Prob. 72AYUCh. 5.3 - Prob. 73AYUCh. 5.3 - Prob. 74AYUCh. 5.3 - Prob. 75AYUCh. 5.3 - Prob. 76AYUCh. 5.3 - Prob. 77AYUCh. 5.3 - Prob. 78AYUCh. 5.3 - Prob. 79AYUCh. 5.3 - Prob. 80AYUCh. 5.3 - Prob. 81AYUCh. 5.3 - Prob. 82AYUCh. 5.3 - Prob. 83AYUCh. 5.3 - Prob. 84AYUCh. 5.3 - Prob. 85AYUCh. 5.3 - Prob. 86AYUCh. 5.3 - Prob. 87AYUCh. 5.3 - Prob. 88AYUCh. 5.3 - Prob. 89AYUCh. 5.3 - Prob. 90AYUCh. 5.3 - Prob. 91AYUCh. 5.3 - Prob. 92AYUCh. 5.3 - Prob. 93AYUCh. 5.3 - Prob. 94AYUCh. 5.3 - Prob. 95AYUCh. 5.3 - Prob. 96AYUCh. 5.3 - Prob. 97AYUCh. 5.3 - Prob. 98AYUCh. 5.3 - Prob. 99AYUCh. 5.3 - Prob. 100AYUCh. 5.3 - Prob. 101AYUCh. 5.3 - Prob. 102AYUCh. 5.3 - Prob. 103AYUCh. 5.3 - Prob. 104AYUCh. 5.3 - Prob. 105AYUCh. 5.3 - Prob. 106AYUCh. 5.3 - Prob. 107AYUCh. 5.3 - Prob. 108AYUCh. 5.3 - Prob. 109AYUCh. 5.3 - Prob. 110AYUCh. 5.3 - Prob. 111AYUCh. 5.3 - Prob. 112AYUCh. 5.3 - Prob. 113AYUCh. 5.3 - Prob. 114AYUCh. 5.3 - Prob. 115AYUCh. 5.3 - Prob. 116AYUCh. 5.3 - Prob. 117AYUCh. 5.3 - Prob. 118AYUCh. 5.3 - Prob. 119AYUCh. 5.3 - Prob. 120AYUCh. 5.3 - Prob. 121AYUCh. 5.3 - Prob. 122AYUCh. 5.3 - Prob. 123AYUCh. 5.3 - Prob. 124AYUCh. 5.3 - Prob. 125AYUCh. 5.3 - Prob. 126AYUCh. 5.3 - Prob. 127AYUCh. 5.3 - Prob. 128AYUCh. 5.3 - Prob. 129AYUCh. 5.4 - Solve each inequality: (a) 3x782x (pp.A79-A80) (b)...Ch. 5.4 - Solve the inequality: x1 x+4 0 (pp. 245-247)Ch. 5.4 - Solve: 2x+3=9 (pp. A44-A46)Ch. 5.4 - The domain of the logarithmic function f( x )= log...Ch. 5.4 - The graph of every logarithmic function f( x )=...Ch. 5.4 - If the graph of a logarithmic function f( x )= log...Ch. 5.4 - True or False If y= log a x , then y= a x .Ch. 5.4 - True or False The graph of f(x)=logax , where...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 11-18, change each exponential...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 19-26, change each logarithmic...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 27-38, find the exact value of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 39—50, find the domain of each...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - In Problems 51-58, use a calculator to evaluate...Ch. 5.4 - Find a so that the graph of f( x ) =log a x...Ch. 5.4 - Find a so that the graph of f( x ) =log a x...Ch. 5.4 - In Problems 61-64, graph each function and its...Ch. 5.4 - In Problems 61-64, graph each function and its...Ch. 5.4 - In Problems 61-64, graph each function and its...Ch. 5.4 - In Problems 61-64, graph each function and its...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 65-72, the graph of a logarithmic...Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 73-88, use the given function f . a....Ch. 5.4 - In Problems 89-112, solve each equation. log 3 x=2Ch. 5.4 - In Problems 89-112, solve each equation. log 5 x=3Ch. 5.4 - In Problems 89-112, solve each equation. log 2...Ch. 5.4 - In Problems 89-112, solve each equation. log 3...Ch. 5.4 - In Problems 89-112, solve each equation. log x 4=2Ch. 5.4 - In Problems 89-112, solve each equation. log x ( 1...Ch. 5.4 - In Problems 89-112, solve each equation. ln e x =5Ch. 5.4 - In Problems 89-112, solve each equation. ln e 2x...Ch. 5.4 - In Problems 89-112, solve each equation. log 4...Ch. 5.4 - In Problems 89-112, solve each equation. log 5...Ch. 5.4 - In Problems 89-112, solve each equation. log 3...Ch. 5.4 - In Problems 89-112, solve each equation. log 6...Ch. 5.4 - In Problems 89-112, solve each equation. e 3x =10Ch. 5.4 - In Problems 89-112, solve each equation. e 2x = 1...Ch. 5.4 - In Problems 89-112, solve each equation. e 2x+5 =8Ch. 5.4 - In Problems 89-112, solve each equation. e 2x+1...Ch. 5.4 - In Problems 89-112, solve each equation. log 3 ( x...Ch. 5.4 - In Problems 89-112, solve each equation. log 5 ( x...Ch. 5.4 - In Problems 89-112, solve each equation. log 2 8 x...Ch. 5.4 - In Problems 89-112, solve each equation. log 3 3 x...Ch. 5.4 - In Problems 89-112, solve each equation. 5 e 0.2x...Ch. 5.4 - In Problems 89-112, solve each equation. 8 10 2x7 ...Ch. 5.4 - In Problems 89-112, solve each equation. 2 10 2x...Ch. 5.4 - In Problems 89-112, solve each equation. 4 e x+1...Ch. 5.4 - Suppose that G( x )= log 3 ( 2x+1 )2 . a. What is...Ch. 5.4 - Suppose that F(x)= log 2 ( x+1 )3 . a. What is the...Ch. 5.4 - In Problems 115-118, graph each function. Based on...Ch. 5.4 - In Problems 115-118, graph each function. Based on...Ch. 5.4 - In Problems 115-118, graph each function. Based on...Ch. 5.4 - In Problems 115-118, graph each function. Based on...Ch. 5.4 - Prob. 117AYUCh. 5.4 - Prob. 118AYUCh. 5.4 - Prob. 119AYUCh. 5.4 - Prob. 120AYUCh. 5.4 - Prob. 121AYUCh. 5.4 - Prob. 122AYUCh. 5.4 - Prob. 123AYUCh. 5.4 - Prob. 124AYUCh. 5.4 - Prob. 125AYUCh. 5.4 - Prob. 126AYUCh. 5.4 - Prob. 127AYUCh. 5.4 - Prob. 128AYUCh. 5.4 - Prob. 129AYUCh. 5.4 - Prob. 130AYUCh. 5.4 - Prob. 131AYUCh. 5.4 - Prob. 132AYUCh. 5.4 - Prob. 133AYUCh. 5.4 - Prob. 134AYUCh. 5.4 - Prob. 135AYUCh. 5.4 - Prob. 136AYUCh. 5.5 - Prob. 1AYUCh. 5.5 - Prob. 2AYUCh. 5.5 - Prob. 3AYUCh. 5.5 - Prob. 4AYUCh. 5.5 - Prob. 5AYUCh. 5.5 - Prob. 6AYUCh. 5.5 - Prob. 7AYUCh. 5.5 - Prob. 8AYUCh. 5.5 - Prob. 9AYUCh. 5.5 - Prob. 10AYUCh. 5.5 - Prob. 11AYUCh. 5.5 - Prob. 12AYUCh. 5.5 - Prob. 13AYUCh. 5.5 - Prob. 14AYUCh. 5.5 - Prob. 15AYUCh. 5.5 - Prob. 16AYUCh. 5.5 - Prob. 17AYUCh. 5.5 - Prob. 18AYUCh. 5.5 - Prob. 19AYUCh. 5.5 - Prob. 20AYUCh. 5.5 - Prob. 21AYUCh. 5.5 - Prob. 22AYUCh. 5.5 - Prob. 23AYUCh. 5.5 - Prob. 24AYUCh. 5.5 - Prob. 25AYUCh. 5.5 - Prob. 26AYUCh. 5.5 - Prob. 27AYUCh. 5.5 - Prob. 28AYUCh. 5.5 - Prob. 29AYUCh. 5.5 - Prob. 30AYUCh. 5.5 - Prob. 31AYUCh. 5.5 - Prob. 32AYUCh. 5.5 - Prob. 33AYUCh. 5.5 - Prob. 34AYUCh. 5.5 - Prob. 35AYUCh. 5.5 - Prob. 36AYUCh. 5.5 - Prob. 37AYUCh. 5.5 - Prob. 38AYUCh. 5.5 - Prob. 39AYUCh. 5.5 - Prob. 40AYUCh. 5.5 - Prob. 41AYUCh. 5.5 - Prob. 42AYUCh. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 37-56, write each expression as a sum...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 57-70, write each expression as a...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 71-78, use the Change-of-Base Formula...Ch. 5.5 - In Problems 79-84, graph each function using a...Ch. 5.5 - In Problems 79-84, graph each function using a...Ch. 5.5 - In Problems 79-84, graph each function using a...Ch. 5.5 - In Problems 79-84, graph each function using a...Ch. 5.5 - In Problems 79-84, graph each function using a...Ch. 5.5 - In Problems 79-84, graph each function using a...Ch. 5.5 - If f(x)=lnx , lnx,g(x)= e x , and h(x)= x 2 ,...Ch. 5.5 - If f(x)= log 2 x , g(x)= 2 x , and h(x)=4x , find:...Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - In Problems 87-96, express y as a function of x....Ch. 5.5 - Find the value of log 2 3 log 3 4 log 4 5 log 5 6...Ch. 5.5 - Find the value of log 2 4 log 4 6 log 6 8 .Ch. 5.5 - Find the value of log 2 3 log 3 4 log n (n+1) log...Ch. 5.5 - Find the value of log 2 2 log 2 4 log 2 2 n .Ch. 5.5 - Show that log a (x+ x 2 1 )+lo g a (x x 2 1 )=0 .Ch. 5.5 - Show that log a ( x + x1 )+lo g a ( x x1 )=0 .Ch. 5.5 - Show that ln(1+ e 2x )=2x+ln(1+ e 2x ) .Ch. 5.5 - Difference Quotient If f(x)=lo g a x , show that...Ch. 5.5 - If f(x)=lo g a x , show that f(x)=lo g 1/a x .Ch. 5.5 - If f(x)=lo g a xCh. 5.5 - 107. If f(x)=lo g a x , show that f( 1 x )=f(x)Ch. 5.5 - 108. If f(x)=lo g a x , show that f( x )=f(x)Ch. 5.5 - 109. Show that log a ( M N )= log a Mlo g a N ,...Ch. 5.5 - 110. Show that log a ( 1 N )= log a N , where a...Ch. 5.5 - 111. Graph Y 1 =log( x 2 ) and Y 2 =2log(x) using...Ch. 5.5 - 112. Write an example that illustrates why (lo g a...Ch. 5.5 - 113. Write an example that illustrates why log 2...Ch. 5.5 - 114. Does 3 log 3 (5)=5 ? Why or why not?Ch. 5.6 - Solve x 2 7x30=0 . (pp.A47-A52)Ch. 5.6 - Solve (x+3) 2 4(x+3)+3=0 .(pp. A52-A53)Ch. 5.6 - Approximate the solution(s) to x 3 = x 2 5 using a...Ch. 5.6 - Approximate the solution(s) to x 3 2x+2=0 using a...Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - ln Problems 5-40, solve each logarithmic equation....Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 41-68, solve each exponential...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 69-82, use a graphing utility to solve...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - In Problems 83-94, solve each equation. Express...Ch. 5.6 - f( x )= log 2 ( x+3 ) and g( x )= log 2 ( 3x+1 ) ....Ch. 5.6 - f( x )= log 3 ( x+5 ) and g( x )= log 3 ( x1 ) (a)...Ch. 5.6 - (a) If f( x )= 3 x+1 and g( x )= 2 x+2 , graph f...Ch. 5.6 - (a) If f( x )= 5 x1 and g( x )= 2 x+1 , graph f...Ch. 5.6 - (a) Graph f( x )= 3 x and g( x )=10 on the same...Ch. 5.6 - (a) Graph f( x )= 2 x and g( x )=12 on the same...Ch. 5.6 - (a) Graph f( x )= 2 x+1 and g( x )= 2 x+2 on the...Ch. 5.6 - (a) Graph f( x )= 3 x+1 and g( x )= 3 x2 on the...Ch. 5.6 - (a) Graph f( x )= 2 x 4 . (b) Find the zero of f ....Ch. 5.6 - (a) Graph g( x )= 3 x 9 . (b) Find the zero of g ....Ch. 5.6 - A Population Model The resident population of the...Ch. 5.6 - A Population Model The population of the world in...Ch. 5.6 - Depreciation The value V of a Chevy Cruze LS that...Ch. 5.6 - Depreciation The value V of a Honda Civic SE that...Ch. 5.6 - Fill in the reason for each step in the following...Ch. 5.7 - What is the interest due if 500 is borrowed for 6...Ch. 5.7 - If you borrow 5000 and, after 9 months, pay off...Ch. 5.7 - The total amount borrowed (whether by an...Ch. 5.7 - If a principal of P dollars is borrowed for a...Ch. 5.7 - In working problems involving interest, if the...Ch. 5.7 - The ___ ___ ___ ___ is the equivalent annual...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 7-14, find the amount that results...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 15-22, find the principal needed now...Ch. 5.7 - In Problems 23—26, find the effective rate of...Ch. 5.7 - In Problems 23—26, find the effective rate of...Ch. 5.7 - In Problems 23—26, find the effective rate of...Ch. 5.7 - In Problems 23—26, find the effective rate of...Ch. 5.7 - In Problems 27-30, determine the rate that...Ch. 5.7 - In Problems 27-30, determine the rate that...Ch. 5.7 - In Problems 27-30, determine the rate that...Ch. 5.7 - In Problems 27-30, determine the rate that...Ch. 5.7 - What rate of interest compounded annually is...Ch. 5.7 - What rate of interest compounded annually is...Ch. 5.7 - What rate of interest compounded annually is...Ch. 5.7 - What rate of interest compounded annually is...Ch. 5.7 - (a) How long does it take for an investment to...Ch. 5.7 - (a) How long does it take for an investment to...Ch. 5.7 - What rate of interest compounded quarterly will...Ch. 5.7 - What rate of interest compounded continuously will...Ch. 5.7 - Time Required to Reach a Goal If Tanisha has 100...Ch. 5.7 - Time Required to Reach a Goal If Angela has 100 to...Ch. 5.7 - Time Required to Reach a Goal How many years will...Ch. 5.7 - Time Required to Reach a Goal how many years will...Ch. 5.7 - Price Appreciation of Homes What will a 90,000...Ch. 5.7 - Credit Card Interest A department store charges...Ch. 5.7 - Saving for a Car Jerome will be buying a used car...Ch. 5.7 - Paying off a Loan John requires 3000 in 6 months...Ch. 5.7 - Return on a Stock George contemplates the purchase...Ch. 5.7 - Return on an Investment A business purchased for...Ch. 5.7 - Comparing Savings Plans Jim places 1000 in a bank...Ch. 5.7 - Savings Plans On January 1, Kim places 1000 in a...Ch. 5.7 - Comparing IRA Investments Will invests 2000 in his...Ch. 5.7 - Comparing Two Alternatives Suppose that April has...Ch. 5.7 - College Costs The average annual cost of college...Ch. 5.7 - Analyzing Interest Rates on a Mortgage Colleen and...Ch. 5.7 - 2009 Federal stimulus Package In February 2009,...Ch. 5.7 - Per Capita Federal Debt In 2015, the federal debt...Ch. 5.7 - Inflation Problems 57-62 require the following...Ch. 5.7 - Inflation Problems 57-62 require the following...Ch. 5.7 - Inflation Problems 57-62 require the following...Ch. 5.7 - Inflation Problems 57-62 require the following...Ch. 5.7 - Inflation Problems 57-62 require the following...Ch. 5.7 - Inflation Problems 57-62 require the following...Ch. 5.7 - Problems 63-66 involve zero-coupon bonds. A...Ch. 5.7 - Problems 63-66 involve zero-coupon bonds. A...Ch. 5.7 - Problems 63-66 involve zero-coupon bonds. A...Ch. 5.7 - Problems 63-66 involve zero-coupon bonds. A...Ch. 5.7 - Time to Double or Triple an Investment The formula...Ch. 5.7 - Time to Reach an Investment Goal The formula t=...Ch. 5.7 - Problems 69-72 require the following discussion....Ch. 5.7 - Problems 69-72 require the following discussion....Ch. 5.7 - Problems 69-72 require the following discussion....Ch. 5.7 - Problems 69-72 require the following discussion....Ch. 5.7 - Explain in your own words what the term compound...Ch. 5.7 - Explain in your own words the meaning of present...Ch. 5.7 - Critical Thinking You have just contracted to buy...Ch. 5.8 - Prob. 1AYUCh. 5.8 - Prob. 2AYUCh. 5.8 - Prob. 3AYUCh. 5.8 - Prob. 4AYUCh. 5.8 - Prob. 5AYUCh. 5.8 - Prob. 6AYUCh. 5.8 - Prob. 7AYUCh. 5.8 - Prob. 8AYUCh. 5.8 - Prob. 9AYUCh. 5.8 - Prob. 10AYUCh. 5.8 - Prob. 11AYUCh. 5.8 - Prob. 12AYUCh. 5.8 - Prob. 13AYUCh. 5.8 - Prob. 14AYUCh. 5.8 - Prob. 15AYUCh. 5.8 - Prob. 16AYUCh. 5.8 - Prob. 17AYUCh. 5.8 - Prob. 18AYUCh. 5.8 - Prob. 19AYUCh. 5.8 - Prob. 20AYUCh. 5.8 - Prob. 21AYUCh. 5.8 - Prob. 22AYUCh. 5.8 - Prob. 23AYUCh. 5.8 - Prob. 24AYUCh. 5.8 - Prob. 25AYUCh. 5.8 - Prob. 26AYUCh. 5.8 - Prob. 27AYUCh. 5.8 - Prob. 28AYUCh. 5.8 - Prob. 29AYUCh. 5.9 - Prob. 1AYUCh. 5.9 - Prob. 2AYUCh. 5.9 - Prob. 3AYUCh. 5.9 - Prob. 4AYUCh. 5.9 - Prob. 5AYUCh. 5.9 - Prob. 6AYUCh. 5.9 - Prob. 7AYUCh. 5.9 - Prob. 8AYUCh. 5.9 - Prob. 9AYUCh. 5.9 - Prob. 10AYUCh. 5.9 - Prob. 11AYUCh. 5.9 - Prob. 12AYUCh. 5.9 - Prob. 13AYUCh. 5 - Evaluate each expression using the graphs of y=f(...Ch. 5 - In Problems 2 4, for the given functions f and g...Ch. 5 - In Problems 2 4, for the given functions f and g...Ch. 5 - In Problems 2 4, for the given functions f and g...Ch. 5 - In Problems 5-7, find fg,gf,ff, and gg for each...Ch. 5 - In Problems 5-7, find fg,gf,ff, and gg for each...Ch. 5 - In Problems 5-7, find fg,gf,ff, and gg for each...Ch. 5 - In Problem 8, (a) verify that the function is...Ch. 5 - In Problem 9, state why the graph of the function...Ch. 5 - In Problems 10-13, the function f is one-to-one....Ch. 5 - In Problems 10-13, the function f is one-to-one....Ch. 5 - In Problems 10-13, the function f is one-to-one....Ch. 5 - In Problems 10-13, the function f is one-to-one....Ch. 5 - In Problem 14, f( x ) =3 x andg( x ) =log 3 x...Ch. 5 - Convert 5 2 =z to an equivalent statement...Ch. 5 - Convert log 5 u13 to an equivalent statement...Ch. 5 - In Problems 17 and 18, find the domain of each...Ch. 5 - In Problems 17 and 18, find the domain of each...Ch. 5 - In Problems 19-21, evaluate each expression. Do...Ch. 5 - Prob. 20RECh. 5 - In Problems 19-21, evaluate each expression. Do...Ch. 5 - In Problems 22-25, write each expression as the...Ch. 5 - In Problems 22-25, write each expression as the...Ch. 5 - In Problems 22-25, write each expression as the...Ch. 5 - In Problems 22-25, write each expression as the...Ch. 5 - In Problems 26-28, write each expression as a...Ch. 5 - In Problems 26-28, write each expression as a...Ch. 5 - In Problems 26-28, write each expression as a...Ch. 5 - Use the Change-of-Base Formula and a calculator to...Ch. 5 - Graph y= log 3 x using a graphing utility and the...Ch. 5 - In Problems 31-34, use the given function f to:...Ch. 5 - In Problems 31-34, use the given function f to:...Ch. 5 - In Problems 31-34, use the given function f to:...Ch. 5 - In Problems 31-34, use the given function f to:...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - In Problems 35-45, solve each equation. Express...Ch. 5 - Suppose that f( x )= log 2 (x2)+1 . (a) Graph f...Ch. 5 - Amplifying Sound An amplifier’s power output P...Ch. 5 - Limiting Magnitude of a Telescope A telescope is...Ch. 5 - Salvage Value The number of years n for a piece of...Ch. 5 - Funding a College Education A child's grandparents...Ch. 5 - Funding a College Education A child's grandparents...Ch. 5 - Estimating the Dale That a Prehistoric Man Died...Ch. 5 - Temperature of a Skillet A skillet is removed from...Ch. 5 - World Population The annual growth rate of the...Ch. 5 - Radioactive Decay The half-life of cobalt is 5.27...Ch. 5 - Logistic Growth The logistic growth model Pt= 0.8...Ch. 5 - Rising Tuition The following data represent the...Ch. 5 - Wind Chill Factor the following data represent the...Ch. 5 - Spreading of a Disease Jack and Diane live in a...Ch. 5 - Prob. 1CTCh. 5 - Prob. 2CTCh. 5 - Prob. 3CTCh. 5 - Prob. 4CTCh. 5 - Prob. 5CTCh. 5 - Prob. 6CTCh. 5 - Prob. 7CTCh. 5 - Prob. 8CTCh. 5 - Prob. 9CTCh. 5 - Prob. 10CTCh. 5 - Prob. 11CTCh. 5 - Prob. 12CTCh. 5 - Prob. 13CTCh. 5 - Prob. 14CTCh. 5 - Prob. 15CTCh. 5 - Prob. 16CTCh. 5 - Prob. 17CTCh. 5 - Prob. 18CTCh. 5 - Prob. 19CTCh. 5 - Prob. 20CTCh. 5 - Prob. 21CTCh. 5 - Prob. 22CTCh. 5 - Prob. 23CTCh. 5 - Prob. 1CRCh. 5 - Prob. 2CRCh. 5 - Prob. 3CRCh. 5 - Prob. 4CRCh. 5 - Prob. 5CRCh. 5 - Prob. 6CRCh. 5 - Prob. 7CRCh. 5 - Prob. 8CRCh. 5 - Prob. 9CRCh. 5 - Prob. 10CRCh. 5 - Prob. 11CRCh. 5 - Prob. 12CRCh. 5 - Prob. 13CRCh. 5 - Prob. 14CRCh. 5 - Prob. 15CRCh. 5 - Prob. 16CR
Additional Math Textbook Solutions
Find more solutions based on key concepts
Fill in each blanks so that the resulting statement is true. Any set of ordered pairs is called a/an _______. T...
College Algebra (7th Edition)
Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...
College Algebra with Modeling & Visualization (5th Edition)
Standard Normal Distribution. In Exercises 17–36, assume that a randomly selected subject is given a bone densi...
Elementary Statistics (13th Edition)
Fill in each blank so that the resulting statement is true. Any set of ordered pairs is called a/an ____.The se...
Algebra and Trigonometry (6th Edition)
The four flaws in the given survey.
Elementary Statistics
In Exercises 1–6, find the average rate of change of the function over the given interval or intervals.
3.
University Calculus: Early Transcendentals (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Evaluate the definite integral using the given integration limits and the limits obtained by trigonometric substitution. 14 x² dx 249 (a) the given integration limits (b) the limits obtained by trigonometric substitutionarrow_forwardAssignment #1 Q1: Test the following series for convergence. Specify the test you use: 1 n+5 (-1)n a) Σn=o √n²+1 b) Σn=1 n√n+3 c) Σn=1 (2n+1)3 3n 1 d) Σn=1 3n-1 e) Σn=1 4+4narrow_forwardanswer problem 1a, 1b, 1c, 1d, and 1e and show work/ explain how you got the answerarrow_forward
- Provethat a) prove that for any irrational numbers there exists? asequence of rational numbers Xn converg to S. b) let S: RR be a sunctions-t. f(x)=(x-1) arc tan (x), xe Q 3(x-1) 1+x² x&Q Show that lim f(x)= 0 14x C) For any set A define the set -A=yarrow_forwardQ2: Find the interval and radius of convergence for the following series: Σ n=1 (-1)η-1 xn narrow_forward8. Evaluate arctan x dx a) xartanx 2 2 In(1 + x²) + C b) xartanx + 1½-3ln(1 + x²) + C c) xartanx + In(1 + x²) + C d) (arctanx)² + C 2 9) Evaluate Inx³ dx 3 a) +C b) ln x² + C c)¾½ (lnx)² d) 3x(lnx − 1) + C - x 10) Determine which integral is obtained when the substitution x = So¹² √1 - x²dx sine is made in the integral πT π π a) √ sin cos e de b) √ cos² de c) c Ꮎ Ꮎ cos² 0 de c) cos e de d) for cos² e de πT 11. Evaluate tan³xdx 1 a) b) c) [1 - In 2] 2 2 c) [1 − In2] d)½½[1+ In 2]arrow_forward12. Evaluate ſ √9-x2 -dx. x2 a) C 9-x2 √9-x2 - x2 b) C - x x arcsin ½-½ c) C + √9 - x² + arcsin x d) C + √9-x2 x2 13. Find the indefinite integral S cos³30 √sin 30 dᎾ . 2√√sin 30 (5+sin²30) √sin 30 (3+sin²30) a) C+ √sin 30(5-sin²30) b) C + c) C + 5 5 5 10 d) C + 2√√sin 30 (3-sin²30) 2√√sin 30 (5-sin²30) e) C + 5 15 14. Find the indefinite integral ( sin³ 4xcos 44xdx. a) C+ (7-5cos24x)cos54x b) C (7-5cos24x)cos54x (7-5cos24x)cos54x - 140 c) C - 120 140 d) C+ (7-5cos24x)cos54x e) C (7-5cos24x)cos54x 4 4 15. Find the indefinite integral S 2x2 dx. ex - a) C+ (x²+2x+2)ex b) C (x² + 2x + 2)e-* d) C2(x²+2x+2)e¯* e) C + 2(x² + 2x + 2)e¯* - c) C2x(x²+2x+2)e¯*arrow_forward4. Which substitution would you use to simplify the following integrand? S a) x = sin b) x = 2 tan 0 c) x = 2 sec 3√√3 3 x3 5. After making the substitution x = = tan 0, the definite integral 2 2 3 a) ៖ ស្លឺ sin s π - dᎾ 16 0 cos20 b) 2/4 10 cos 20 π sin30 6 - dᎾ c) Π 1 cos³0 3 · de 16 0 sin20 1 x²√x²+4 3 (4x²+9)2 π d) cos²8 16 0 sin³0 dx d) x = tan 0 dx simplifies to: de 6. In order to evaluate (tan 5xsec7xdx, which would be the most appropriate strategy? a) Separate a sec²x factor b) Separate a tan²x factor c) Separate a tan xsecx factor 7. Evaluate 3x x+4 - dx 1 a) 3x+41nx + 4 + C b) 31n|x + 4 + C c) 3 ln x + 4+ C d) 3x - 12 In|x + 4| + C x+4arrow_forward1. Abel's Theorem. The goal in this problem is to prove Abel's theorem by following a series of steps (each step must be justified). Theorem 0.1 (Abel's Theorem). If y1 and y2 are solutions of the differential equation y" + p(t) y′ + q(t) y = 0, where p and q are continuous on an open interval, then the Wronskian is given by W (¥1, v2)(t) = c exp(− [p(t) dt), where C is a constant that does not depend on t. Moreover, either W (y1, y2)(t) = 0 for every t in I or W (y1, y2)(t) = 0 for every t in I. 1. (a) From the two equations (which follow from the hypotheses), show that y" + p(t) y₁ + q(t) y₁ = 0 and y½ + p(t) y2 + q(t) y2 = 0, 2. (b) Observe that Hence, conclude that (YY2 - Y1 y2) + P(t) (y₁ Y2 - Y1 Y2) = 0. W'(y1, y2)(t) = yY2 - Y1 y2- W' + p(t) W = 0. 3. (c) Use the result from the previous step to complete the proof of the theorem.arrow_forward2. Observations on the Wronskian. Suppose the functions y₁ and y2 are solutions to the differential equation p(x)y" + q(x)y' + r(x) y = 0 on an open interval I. 1. (a) Prove that if y₁ and y2 both vanish at the same point in I, then y₁ and y2 cannot form a fundamental set of solutions. 2. (b) Prove that if y₁ and y2 both attain a maximum or minimum at the same point in I, then y₁ and Y2 cannot form a fundamental set of solutions. 3. (c) show that the functions & and t² are linearly independent on the interval (−1, 1). Verify that both are solutions to the differential equation t² y″ – 2ty' + 2y = 0. Then justify why this does not contradict Abel's theorem. 4. (d) What can you conclude about the possibility that t and t² are solutions to the differential equation y" + q(x) y′ + r(x)y = 0?arrow_forwardQuestion 4 Find an equation of (a) The plane through the point (2, 0, 1) and perpendicular to the line x = y=2-t, z=3+4t. 3t, (b) The plane through the point (3, −2, 8) and parallel to the plane z = x+y. (c) The plane that contains the line x = 1+t, y = 2 − t, z = 4 - 3t and is parallel to the plane 5x + 2y + z = 1. (d) The plane that passes through the point (1,2,3) and contains the line x = 3t, y = 1+t, and z = 2-t. (e) The plane that contains the lines L₁: x = 1 + t, y = 1 − t, z = 2t and L2 : x = 2 − s, y = s, z = 2.arrow_forwardPlease find all values of x.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Implicit Differentiation with Transcendental Functions; Author: Mathispower4u;https://www.youtube.com/watch?v=16WoO59R88w;License: Standard YouTube License, CC-BY
How to determine the difference between an algebraic and transcendental expression; Author: Study Force;https://www.youtube.com/watch?v=xRht10w7ZOE;License: Standard YouTube License, CC-BY