Chapter 5, Problem 5.5.1P

To determine

(a)

Maximum permissible load using LFRD method.

Answer to Problem 5.5.1P

The maximum permissible load from LFRD method is $\text{P}\text{=}\text{29}\text{.34}\text{kips-ft}$.

Explanation of Solution

Given information:

A W 10X 77 has continuous lateral support. The load P is a service live load and $F_y=50\text{ksi}$.

Following is the given beam:

Calculation:

We have following properties for W 10X 77 from ASIC manual

DesignationImperial (in x lb/ft)	Depth h (in)	Width w (in)	Web Thickness tw (in)	Flange Thickness tf (in)	Sectional Area (in2)	Weight (lbf/ft)	Static Parameters
							Moment of Inertia		Elastic Section Modulus
							Ix (in4)	Iy (in4)	Sx (in3)	Sy (in3)
W 10 x 77	10.60	10.190	0.530	0.870	22.6	77	455	154	85.9	30.1

Let’s check for the compactness of the given W-shape beam using part $1$ of ASIC manual

For Flange:

$\frac{b_f}{2\times t_f}<0.38\times \left[\sqrt{\frac{E}{F_y}}\right]$

Where, $F_y$ is the characteristic strength of steel, E is the modulus of elasticity, $b_f$ is the width of flange and $t_f$ is the thickness of the flange.

If the above condition satisfies, then the flange is non compact for flexure

$\begin{array}{l}\text{Substitute 29000 for E, 50 for }{F}_y\\ \frac{b_f}{2t_f}<0.38\sqrt{\frac{E}{F_y}}\\ \frac{10.190}{2\times 0.870}<0.38\times \sqrt{\frac{29000}{50}}\\ 5.86<9.15\\ \text{Therefore, flange is compact}\text{.}\\ \text{So, the condition to check whether a web is non compact for flexure}\\ \frac{h}{t_w}<0.376\sqrt{\frac{E}{F_y}}\\ \frac{10.60}{0.530}<0.376\sqrt{\frac{29000}{50}}\\ 20<90.6.\end{array}$

Therefore, the web is compact.

Calculate the nominal flexural strength using the formula

$M_n=M_p=F_y{Z}_x$

Where, $Z$ is the plastic modulus of W-section and is equal to $\text{96}\text{.66}i{n}^3,$ it could be found in ASIC

Manual.

$\begin{array}{l}\text{Substitute 96}\text{.66}i{n}^3\text{ for }{Z}_x,50{\text{ksi for F}}_y\\ M_n=M_p=F_y{Z}_x\\ M_n=M_p=F_y{Z}_x\text{ =}\text{50ksi(96}\text{.66}i{n}^3\text{)}\end{array}$

$M_n=F_y{Z}_x\text{=}\text{4833}\text{in-kips}$

$M_n=F_y{Z}_x\text{=}\text{402}\text{.75}\text{ft-kips}\text{.}$

Now, calculate the maximum bending moment due to dead load, we have

$w_D=77\frac{lb}{ft}$

Maximum bending moment for a simply supported beam carrying a dead UDL

${\text{M}}_D=\frac{\left(w_D\times l^2\right)}{8}$

Where, $w_D$ is uniformly distributed load and $l$ is the length of the beam.

Substitute, $w_D=77\frac{lb}{ft}$ and $l=30ft$.

${\text{M}}_D=\frac{\left(w_D\times l^2\right)}{8}.$

$\begin{array}{l}{\text{M}}_D=\frac{\left(77\frac{lb}{ft}\times {\left(30ft\right)}^2\right)}{8}\\ {\text{M}}_D=\frac{\left(0.077\text{}\text{}\frac{Kips}{ft}\times 900f{t}^2\right)}{8}\\ {\text{M}}_D=\frac{\left(69.30Kipsft\right)}{8}\\ {\text{M}}_D=8.6625Kipsft.\end{array}$

Calculate the maximum bending moment for a simply supported beam carrying a concentrated

live load of the beam:

$M_L=\frac{P\times l}{4}$

Where, P is the concentrated load and L is the length of the beam is.

$\begin{array}{l}{M}_L=\frac{P\times l}{4}\\ M_L=\frac{P\times 30}{4}\text{kips}\text{.ft}\\ M_L=\left(7.5P\right)\text{kips}\text{.ft}\text{.}\end{array}$

Now, using Load Resistance and Factored design method:

Calculate the maximum permissible load P.

$M_u=\left(1.2\times M_D\right)+\left(1.6\times M_L\right)$

Substitute ${\text{M}}_D=8.6625Kipsft$ and $M_L=\left(7.5P\right)\text{kips}\text{.ft}$

$\begin{array}{l}{M}_u=\left(1.2\times M_D\right)+\left(1.6\times M_L\right)\\ M_u=\left(1.2\times 8.6625Kipsft\right)+\left(1.6\times \left(7.5P\right)\text{kips}\text{.ft}\right)\end{array}$

Calculate P, by equating the maximum bending moment with the flexural strength of the beam;

$M_u=({\varphi }_b\times M_n)$

Where, ${\varphi }_b$ is the resistance factor.

Substitute $M_n\text{=}\text{402}\text{.75}\text{ft-kips}$ and $M_u=\left(1.2\times 8.6625Kipsft\right)+\left(1.6\times \left(7.5P\right)\text{kips}\text{.ft}\right)$.

$\begin{array}{l}{M}_u=({\varphi }_b\times M_n)\\ \left(1.2\times 8.6625\text{Kips}\text{ft}\right)+\left(1.6\times \left(7.5P\right)\text{kips}\text{.ft}\right)=\left(0.90\times \text{402}\text{.75}\text{ft-kips}\right)\\ 10.395\text{Kips}\text{ft}+12\times P\text{Kips}\text{ft}=\text{362}\text{.475}\text{kips-ft}\text{.}\\ \text{362}\text{.475}\text{kips-ft}-10.395\text{Kips}\text{ft}=12\times P\text{Kips}\text{ft}\text{.}\\ \text{352}\text{.08}\text{kips-ft}=12\times P\text{Kips}\text{ft}\text{.}\\ \text{P}\text{=}\frac{\text{352}\text{.08}\text{kips-ft}}{12}\\ \text{P}\text{=}\text{29}\text{.34}\text{kips-ft}\text{.}\end{array}$

Conclusion:

Therefore, the maximum permissible load from LFRD method is $\text{P}\text{=}\text{29}\text{.34}\text{kips-ft}$.

To determine

(b)

Maximum permissible load using ASD method.

Answer to Problem 5.5.1P

The maximum permissible load from ASD method is $\text{P}\text{=}\text{31}\text{.00}\text{kips-ft}$.

Explanation of Solution

Given information:

A W 10X 77 has continuous lateral support. The load P is a service live load and $F_y=50\text{ksi}$. Following is the given beam

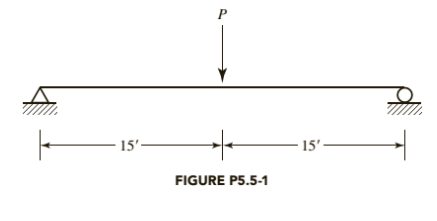
Calculation:

We have following properties for W 10X 77 from ASIC manual

DesignationImperial (in x lb/ft)	Depthh (in)	Widthw (in)	Web Thicknesstw (in)	Flange Thicknesstf (in)	Sectional Area (in2)	Weight (lbf/ft)	Static Parameters
							Moment of Inertia		Elastic Section Modulus
							Ix (in4)	Iy (in4)	Sx (in3)	Sy (in3)
W 10 x 77	10.60	10.190	0.530	0.870	22.6	77	455	154	85.9	30.1

Let’s check for the compactness of the given W-shape beam using part $1$ of ASIC manual

For Flange:

$\frac{b_f}{2\times t_f}<0.38\times \left[\sqrt{\frac{E}{F_y}}\right]$

Where, $F_y$ is the characteristic strength of steel, E is the modulus of elasticity, $b_f$ is the width of flange and $t_f$ is the thickness of the flange.

If the above condition satisfies, then the flange is non compact for flexure

$\begin{array}{l}\text{Substitute 29000 for E, 50 for }{F}_y\\ \frac{b_f}{2t_f}<0.38\sqrt{\frac{E}{F_y}}\\ \frac{10.190}{2\times 0.870}<0.38\times \sqrt{\frac{29000}{50}}\\ 5.86<9.15\\ \text{Therefore, flange is compact}\text{.}\\ \text{So, the condition to check whether a web is non compact for flexure}\\ \frac{h}{t_w}<0.376\sqrt{\frac{E}{F_y}}\\ \frac{10.60}{0.530}<0.376\sqrt{\frac{29000}{50}}\\ 20<90.6.\end{array}$

Therefore, the web is compact.

Calculate the nominal flexural strength using the formula

$M_n=M_p=F_y{Z}_x$

$\begin{array}{l}\text{Substitute 96}\text{.66}i{n}^3\text{ for }{Z}_x,50{\text{ksi for F}}_y\\ M_n=M_p=F_y{Z}_x\\ M_n=M_p=F_y{Z}_x\text{ =}\text{50ksi(96}\text{.66}i{n}^3\text{)}\end{array}$

$M_n=F_y{Z}_x\text{=}\text{4833}\text{in-kips}$

$M_n=F_y{Z}_x\text{=}\text{402}\text{.75}\text{ft-kips}\text{.}$

Now, calculate the maximum bending moment due to dead load, we have

$w_D=77\frac{lb}{ft}$ as per the properties of the given section.

Maximum bending moment for a simply supported beam carrying a dead UDL

${\text{M}}_D=\frac{\left(w_D\times l^2\right)}{8}$

Where, $w_D$ is uniformly distributed load and $l$ is the length of the beam.

Substitute, $w_D=77\frac{lb}{ft}$ and $l=30ft$.

${\text{M}}_D=\frac{\left(w_D\times l^2\right)}{8}.$

$\begin{array}{l}{\text{M}}_D=\frac{\left(77\frac{lb}{ft}\times {\left(30ft\right)}^2\right)}{8}\\ {\text{M}}_D=\frac{\left(0.077\text{}\text{}\frac{Kips}{ft}\times 900f{t}^2\right)}{8}\\ {\text{M}}_D=\frac{\left(69.30Kipsft\right)}{8}\\ {\text{M}}_D=8.6625Kipsft.\end{array}$

Calculate the maximum bending moment for a simply supported beam carrying a concentrated

live load of the beam:

$M_L=\frac{P\times l}{4}$

Where, P is the concentrated load and L is the length of the beam is.

$\begin{array}{l}{M}_L=\frac{P\times l}{4}\\ M_L=\frac{P\times 30}{4}\text{kips}\text{.ft}\\ M_L=\left(7.5P\right)\text{kips}\text{.ft}\text{.}\end{array}$

Calculate the uniformly distributed load on the beam by equating

Allowable stress design method:

$M_a=M_D+M_L$

Substitute ${\text{M}}_D=8.6625Kipsft$ and $M_L=\left(7.5P\right)\text{kips}\text{.ft}$

$\begin{array}{l}{M}_a=M_D+M_L\\ M_a=8.6625Kipsft+\left(7.5P\right)\text{kips}\text{.ft}\text{.}\end{array}$

Calculate P, by equating the maximum bending moment with the flexural strength of the beam:

$M_a=\frac{M_n}{{\Omega }_b}$

Substitute, $M_a=8.6625Kipsft+\left(7.5P\right)\text{kips}\text{.ft}\text{.}$, $M_n\text{=}\text{402}\text{.75}\text{ft-kips}$ and ${\Omega }_b=1.67$.

$\begin{array}{l}{M}_a=\frac{M_n}{\Omega }\\ 8.6625\text{kips}\text{ft}+\left(7.5P\right)\text{kips}\text{.ft}\text{=}\frac{\text{402}\text{.75}\text{ft-kips}}{1.67}\\ 8.6625\text{kips}\text{ft}+\left(7.5P\right)\text{kips}\text{.ft}\text{=}\text{241}\text{.167}\text{ft-kips}\\ 7.5P\text{kips}\text{.ft}\text{=}\text{241}\text{.167}\text{ft-kips}-8.6625\text{kips}\text{ft}\\ 7.5P\text{kips}\text{.ft}\text{=}232.51\text{ft-kips}.\\ P=\frac{232.51\text{ft-kips}}{7.5}.\\ P=31.00\text{kips}\text{.ft}.\end{array}$

Conclusion:

Therefore, the maximum permissible load from ASD method is $\text{P}\text{=}\text{31}\text{.00}\text{kips-ft}$.