Bundle: Physics for Scientists and Engineers with Modern Physics, Loose-leaf Version, 9th + WebAssign Printed Access Card, Multi-Term
9th Edition
ISBN: 9781305932302
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5, Problem 46P
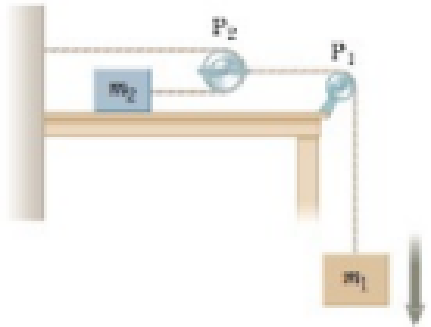
An object of mass m1 hangs from a string that passes over a very light fixed pulley P1 as shown in Figure P5.25. The string connects to a second very light pulley P2. A second string passes around this pulley with one end attached to a wall and the other to an object of mass m2 on a frictionless, horizontal table. (a) If a1 and a2 are the accelerations of m1 and m2, respectively, what is the relation between these accelerations? Find expressions for (b) the tensions in the strings and (c) the accelerations a1 and a2 in terms of the masses m1 and m2 and g.
Figure P5.25
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
ROTATIONAL DYNAMICS
Question 01
A solid circular cylinder and a solid spherical ball of the same mass and radius are rolling
together down the same inclined. Calculate the ratio of their kinetic energy. Assume pure
rolling motion Question 02
A sphere and cylinder of the same mass and radius start from ret at the same point and more
down the same plane inclined at 30° to the horizontal
Which body gets the bottom first and what is its acceleration
b) What angle of inclination of the plane is needed to give the slower body the same
acceleration
Question 03
i)
Define the angular velocity of a rotating body and give its SI unit
A car wheel has its angular velocity changing from 2rads to 30 rads
seconds. If the radius of the wheel is 400mm. calculate
ii)
The angular acceleration
iii)
The tangential linear acceleration of a point on the rim of the wheel
Question 04
in 20
Question B3
Consider the following FLRW spacetime:
t2
ds² = -dt² +
(dx²
+ dy²+ dz²),
t2
where t is a constant.
a)
State whether this universe is spatially open, closed or flat.
[2 marks]
b) Determine the Hubble factor H(t), and represent it in a (roughly drawn) plot as a function
of time t, starting at t = 0.
[3 marks]
c) Taking galaxy A to be located at (x, y, z) = (0,0,0), determine the proper distance to galaxy
B located at (x, y, z) = (L, 0, 0). Determine the recessional velocity of galaxy B with respect
to galaxy A.
d) The Friedmann equations are
2
k
8πG
а
4πG
+
a²
(p+3p).
3
a
3
[5 marks]
Use these equations to determine the energy density p(t) and the pressure p(t) for the
FLRW spacetime specified at the top of the page.
[5 marks]
e) Given the result of question B3.d, state whether the FLRW universe in question is (i)
radiation-dominated, (ii) matter-dominated, (iii) cosmological-constant-dominated, or (iv)
none of the previous. Justify your answer.
f)
[5 marks]
A conformally…
SECTION B
Answer ONLY TWO questions in Section B
[Expect to use one single-sided A4 page for each Section-B sub question.]
Question B1
Consider the line element
where w is a constant.
ds²=-dt²+e2wt dx²,
a) Determine the components of the metric and of the inverse metric.
[2 marks]
b) Determine the Christoffel symbols. [See the Appendix of this document.]
[10 marks]
c)
Write down the geodesic equations.
[5 marks]
d) Show that e2wt it is a constant of geodesic motion.
[4 marks]
e)
Solve the geodesic equations for null geodesics.
[4 marks]
Chapter 5 Solutions
Bundle: Physics for Scientists and Engineers with Modern Physics, Loose-leaf Version, 9th + WebAssign Printed Access Card, Multi-Term
Ch. 5.2 - Which of the following statements is correct? (a)...Ch. 5.4 - An object experiences no acceleration. Which of...Ch. 5.4 - You push an object, initially at rest, across a...Ch. 5.5 - Suppose you are talking by interplanetary...Ch. 5.6 - (i) If a fly collides with the windshield of a...Ch. 5.8 - You press your physics textbook flat against a...Ch. 5.8 - Prob. 5.7QQCh. 5 - The driver of a speeding empty truck slams on the...Ch. 5 - In Figure OQ5.2, a locomotive has broken through...Ch. 5 - Prob. 3OQ
Ch. 5 - Prob. 4OQCh. 5 - Prob. 5OQCh. 5 - The manager of a department store is pushing...Ch. 5 - Two objects are connected by a string that passes...Ch. 5 - Prob. 8OQCh. 5 - A truck loaded with sand accelerates along a...Ch. 5 - A large crate of mass m is place on the flatbed of...Ch. 5 - If an object is in equilibrium, which of the...Ch. 5 - A crate remains stationary after it has been...Ch. 5 - An object of mass m moves with acceleration a down...Ch. 5 - Prob. 1CQCh. 5 - Your hands are wet, and the restroom towel...Ch. 5 - In the motion picture It Happened One Night...Ch. 5 - If a car is traveling due westward with a constant...Ch. 5 - A passenger sitting in the rear of a bus claims...Ch. 5 - A child tosses a ball straight up. She says that...Ch. 5 - A person holds a ball in her hand. (a) Identify...Ch. 5 - Prob. 8CQCh. 5 - Prob. 9CQCh. 5 - Twenty people participate in a tug-of-war. The two...Ch. 5 - Prob. 11CQCh. 5 - Prob. 12CQCh. 5 - A weightlifter stands on a bathroom scale. He...Ch. 5 - Prob. 14CQCh. 5 - Suppose you are driving a classic car. Why should...Ch. 5 - Prob. 16CQCh. 5 - Describe two examples in which the force of...Ch. 5 - The mayor of a city reprimands some city employees...Ch. 5 - Give reasons for the answers to each of the...Ch. 5 - Prob. 20CQCh. 5 - Identify actionreaction pairs in the following...Ch. 5 - Prob. 22CQCh. 5 - Prob. 23CQCh. 5 - A certain orthodontist uses a wire brace to align...Ch. 5 - If a man weighs 900 N on the Earth, what would he...Ch. 5 - A 3.00-kg object undergoes an acceleration given...Ch. 5 - Prob. 4PCh. 5 - Prob. 5PCh. 5 - The average speed of a nitrogen molecule in air is...Ch. 5 - Prob. 7PCh. 5 - Prob. 8PCh. 5 - Review. The gravitational force exerted on a...Ch. 5 - Review. The gravitational force exerted on a...Ch. 5 - Review. An electron of mass 9. 11 1031 kg has an...Ch. 5 - Prob. 12PCh. 5 - One or more external forces, large enough to be...Ch. 5 - A brick of mass M has been placed on a rubber...Ch. 5 - Two forces, F1=(6.00i4.00j)N and...Ch. 5 - Prob. 16PCh. 5 - Prob. 17PCh. 5 - Prob. 18PCh. 5 - Prob. 19PCh. 5 - You stand on the seat of a chair and then hop off....Ch. 5 - Prob. 21PCh. 5 - Review. Three forces acting on an object are given...Ch. 5 - Prob. 23PCh. 5 - Prob. 24PCh. 5 - Review. Figure P5.15 shows a worker poling a boata...Ch. 5 - An iron bolt of mass 65.0 g hangs from a string...Ch. 5 - Prob. 27PCh. 5 - The systems shown in Figure P5.28 are in...Ch. 5 - Prob. 29PCh. 5 - A block slides down a frictionless plane having an...Ch. 5 - The distance between two telephone poles is 50.0...Ch. 5 - A 3.00-kg object is moving in a plane, with its x...Ch. 5 - A bag of cement weighing 325 N hangs in...Ch. 5 - A bag of cement whose weight is Fg hangs in...Ch. 5 - Prob. 35PCh. 5 - Prob. 36PCh. 5 - An object of mass m = 1.00 kg is observed to have...Ch. 5 - Prob. 38PCh. 5 - Prob. 39PCh. 5 - An object of mass m1 = 5.00 kg placed on a...Ch. 5 - Prob. 41PCh. 5 - Two objects are connected by a light string that...Ch. 5 - Prob. 43PCh. 5 - Prob. 44PCh. 5 - In the system shown in Figure P5.23, a horizontal...Ch. 5 - An object of mass m1 hangs from a string that...Ch. 5 - A block is given an initial velocity of 5.00 m/s...Ch. 5 - A car is stuck in the mud. A tow truck pulls on...Ch. 5 - Prob. 49PCh. 5 - Prob. 50PCh. 5 - In Example 5.8, we investigated the apparent...Ch. 5 - Consider a large truck carrying a heavy load, such...Ch. 5 - Prob. 53PCh. 5 - Prob. 54PCh. 5 - A 25.0-kg block is initially at rest on a...Ch. 5 - Why is the following situation impassible? Your...Ch. 5 - Prob. 57PCh. 5 - Before 1960m people believed that the maximum...Ch. 5 - Prob. 59PCh. 5 - A woman at an airport is towing her 20.0-kg...Ch. 5 - Review. A 3.00-kg block starts from rest at the...Ch. 5 - The person in Figure P5.30 weighs 170 lb. As seen...Ch. 5 - A 9.00-kg hanging object is connected by a light,...Ch. 5 - Three objects are connected on a table as shown in...Ch. 5 - Prob. 65PCh. 5 - A block of mass 3.00 kg is pushed up against a...Ch. 5 - Prob. 67PCh. 5 - Prob. 68PCh. 5 - Prob. 69PCh. 5 - A 5.00-kg block is placed on top of a 10.0-kg...Ch. 5 - Prob. 71PCh. 5 - A black aluminum glider floats on a film of air...Ch. 5 - Prob. 73APCh. 5 - Why is the following situation impossible? A book...Ch. 5 - Prob. 75APCh. 5 - A 1.00-kg glider on a horizontal air track is...Ch. 5 - Prob. 77APCh. 5 - Prob. 78APCh. 5 - Two blocks of masses m1 and m2, are placed on a...Ch. 5 - Prob. 80APCh. 5 - An inventive child named Nick wants to reach an...Ch. 5 - Prob. 82APCh. 5 - Prob. 83APCh. 5 - An aluminum block of mass m1 = 2.00 kg and a...Ch. 5 - Prob. 85APCh. 5 - Prob. 86APCh. 5 - Prob. 87APCh. 5 - Prob. 88APCh. 5 - A crate of weight Fg is pushed by a force P on a...Ch. 5 - Prob. 90APCh. 5 - A flat cushion of mass m is released from rest at...Ch. 5 - In Figure P5.46, the pulleys and pulleys the cord...Ch. 5 - What horizontal force must be applied to a large...Ch. 5 - Prob. 94APCh. 5 - A car accelerates down a hill (Fig. P5.95), going...Ch. 5 - Prob. 96CPCh. 5 - Prob. 97CPCh. 5 - Initially, the system of objects shown in Figure...Ch. 5 - A block of mass 2.20 kg is accelerated across a...Ch. 5 - Prob. 100CPCh. 5 - Prob. 101CPCh. 5 - In Figure P5.55, the incline has mass M and is...Ch. 5 - Prob. 103CPCh. 5 - Prob. 104CP
Additional Science Textbook Solutions
Find more solutions based on key concepts
Match the people in column A to their contribution toward the advancement of microbiology, in column B. Column ...
Microbiology: An Introduction
The active ingredient in Tylenol and a host of other over-the-counter pain relievers is acetaminophen (C8H9NO2)...
Chemistry: Atoms First
Why is it necessary to be in a pressurized cabin when flying at 30,000 feet?
Anatomy & Physiology (6th Edition)
Describe the evolution of mammals, tracing their synapsid lineage from early amniote ancestors to true mammals....
Loose Leaf For Integrated Principles Of Zoology
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Page 2 SECTION A Answer ALL questions in Section A [Expect to use one single-sided A4 page for each Section-A sub question.] Question A1 SPA6308 (2024) Consider Minkowski spacetime in Cartesian coordinates th = (t, x, y, z), such that ds² = dt² + dx² + dy² + dz². (a) Consider the vector with components V" = (1,-1,0,0). Determine V and V. V. (b) Consider now the coordinate system x' (u, v, y, z) such that u =t-x, v=t+x. [2 marks] Write down the line element, the metric, the Christoffel symbols and the Riemann curvature tensor in the new coordinates. [See the Appendix of this document.] [5 marks] (c) Determine V", that is, write the object in question A1.a in the coordinate system x'. Verify explicitly that V. V is invariant under the coordinate transformation. Question A2 [5 marks] Suppose that A, is a covector field, and consider the object Fv=AAμ. (a) Show explicitly that F is a tensor, that is, show that it transforms appropriately under a coordinate transformation. [5 marks] (b)…arrow_forwardHow does boiling point of water decreases as the altitude increases?arrow_forwardNo chatgpt pls will upvotearrow_forward
- 14 Z In figure, a closed surface with q=b= 0.4m/ C = 0.6m if the left edge of the closed surface at position X=a, if E is non-uniform and is given by € = (3 + 2x²) ŷ N/C, calculate the (3+2x²) net electric flux leaving the closed surface.arrow_forwardNo chatgpt pls will upvotearrow_forwardsuggest a reason ultrasound cleaning is better than cleaning by hand?arrow_forward
- Checkpoint 4 The figure shows four orientations of an electric di- pole in an external electric field. Rank the orienta- tions according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the di- pole, greatest first. (1) (2) E (4)arrow_forwardWhat is integrated science. What is fractional distillation What is simple distillationarrow_forward19:39 · C Chegg 1 69% ✓ The compound beam is fixed at Ę and supported by rollers at A and B. There are pins at C and D. Take F=1700 lb. (Figure 1) Figure 800 lb ||-5- F 600 lb بتا D E C BO 10 ft 5 ft 4 ft-—— 6 ft — 5 ft- Solved Part A The compound beam is fixed at E and... Hình ảnh có thể có bản quyền. Tìm hiểu thêm Problem A-12 % Chia sẻ kip 800 lb Truy cập ) D Lưu of C 600 lb |-sa+ 10ft 5ft 4ft6ft D E 5 ft- Trying Cheaa Những kết quả này có hữu ích không? There are pins at C and D To F-1200 Egue!) Chegg Solved The compound b... Có Không ☑ ||| Chegg 10 וחarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
Newton's Third Law of Motion: Action and Reaction; Author: Professor Dave explains;https://www.youtube.com/watch?v=y61_VPKH2B4;License: Standard YouTube License, CC-BY