
A short column is made by nailing four 1 × 4-in. planks to a 4 × 4-in. timber. Using an allowable stress of 600 psi, determine the largest compressive load P that can be applied at the center of the top section of the timber column as shown if (a) the column is as described, (b) plank 1 is removed, (c) planks 1 and 2 are removed, (d) planks 1, 2, and 3 are removed, (e) all planks are removed.
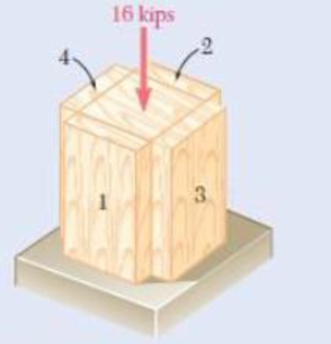
Fig. P4.112
(a)
Find the largest compressive load P that can be applied at the center of the top section of the timber column.
Answer to Problem 112P
The largest compressive load P is
Explanation of Solution
Given information:
The compressive load P is
The allowable stress
The width
The depth
The width
The depth
Calculation:
Sketch the centric loading as shown in Figure 1.
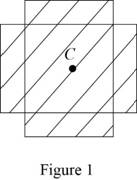
Refer to Figure 1.
Find the area of the timber section using the relation:
Substitute
Calculate the largest compressive load P using the relation:
Substitute
Thus, the largest compressive load P is
(b)
Find the largest compressive load P that can be applied at the center of the top section of the timber column without plank 1.
Answer to Problem 112P
The largest compressive load P that can be applied at the center of the top section of the timber column without plank 1 is
Explanation of Solution
Calculation:
Sketch the Eccentric loading as shown in Figure 2.
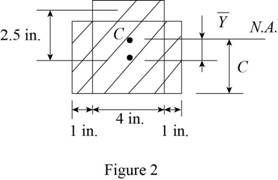
Find the area of the timber section using the relation:
Substitute
Refer to Figure 2.
Find the centroid
Substitute
Refer to Figure 2.
Find the moment of inertia
Substitute
Find the moment of inertia
Substitute
Find the total moment of inertia as follows:
Substitute
Calculate the largest compressive load P that can be applied at the center of the top section of the timber column without plank 1using the relation:
Here, e is the eccentricity, I is the moment of inertia, A is the area of cross section, and c is the distance between the centroid from extreme fibre.
Substitute
Thus, the largest compressive load P that can be applied at the center of the top section of the timber column without plank 1 is
(c)
Find the largest compressive load P that can be applied at the center of the top section of the timber column without plank 1and 2.
Answer to Problem 112P
The largest compressive load P that can be applied at the center of the top section of the timber column without plank 1 and 2 is
Explanation of Solution
Calculation:
Sketch the centric loading as shown in Figure 3.

Refer to Figure 3.
Find the area of the timber section using the relation:
Substitute
Calculate the largest compressive load P using the relation:
Substitute
Thus, the largest compressive load P is
(d)
Find the largest compressive load P that can be applied at the center of the top section of the timber column without plank , 2, and 3.
Answer to Problem 112P
The largest compressive load P that can be applied at the center of the top section of the timber column without plank 1, 2, and 3 is
Explanation of Solution
Calculation:
Sketch the Eccentric loading as shown in Figure 4.
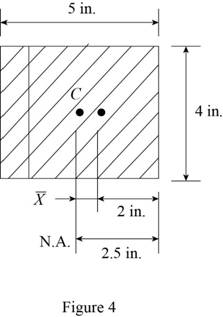
Refer to Figure 4.
Find the area of the timber section using the relation:
Substitute
Find the centroid
Determine the moment of inertia (I) of eccentric section as follows:
Substitute
Calculate the largest compressive load P that can be applied at the center of the top section of the timber column without plank , 2, and 3 using the relation:
Here, e is the eccentricity, I is the moment of inertia, A is the area of cross section, and c is the distance between the centroid from extreme fibre.
Substitute
The largest compressive load P that can be applied at the center of the top section of the timber column without plank 1, 2, and 3 is
(e)
Find the largest compressive load P that can be applied at the center of the top section of the timber all columns are removed.
Answer to Problem 112P
The largest compressive load P that can be applied at the center of the top section of the timber all columns are removed is
Explanation of Solution
Calculation:
Sketch the centric loading as shown in Figure 5.
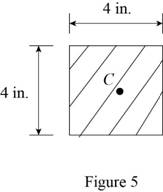
Refer to Figure 5.
Find the area of the timber section using the relation:
Substitute
Calculate the largest compressive load P using the relation:
Substitute
Thus, the largest compressive load P that can be applied at the center of the top section of the timber all columns are removed is
Want to see more full solutions like this?
Chapter 4 Solutions
EBK MECHANICS OF MATERIALS
- Draw left view of the first orthographic projectionarrow_forwardSketch and Describe a timing diagram for a 2 stroke diesel engine emphasis on the 2 stroke as my last answer explained 4 stroke please include a diagram or sketch.arrow_forwardA 4 ft 200 Ib 1000 Ib.ft C 2 ft 350 Ib - за в 2.5 ft 150 Ib 250 Ib 375 300 Ib Replace the force system acting on the frame. shown in the figure by a resultant force (magnitude and direction), and specify where its line of action intersects member (AB), measured from point (A).arrow_forward
- A continuous flow calorimeter was used to obtain the calorific value of a sample of fuel and the following data collected: Mass of fuel: 2.25 kgInlet water temperature: 11 ° COutlet water temperature 60 ° CQuantity of water: 360 Liters Calorimeter efficiency: 85%Calculate the calorific value of the sample ( kJ / kg ). ive submitted this question twice and have gotten two way different answers. looking for some help thanksarrow_forward15 kg of steel ball bearings at 100 ° C is immersed in 25 kg of water at 20 ° C . Assuming no loss of heat to or from the container, calculate the final temperature of the water after equilibrium has been attained.Specific heat of steel: 0.4857 kJ / kg / ° KSpecific heat of water: 4.187 kJ / kg / ° Karrow_forwardSketch and explain a PV Diagram and a Temperature Entropy Diagram for a 4 stroke diesel enginearrow_forward
- A continuous flow calorimeter was used to obtain the calorific value of a sample of fuel and the following data collected: Mass of fuel: 2.25 kgInlet water temperature: 11 ° COutlet water temperature 60 ° CQuantity of water: 360 Liters Calorimeter efficiency: 85%Calculate the calorific value of the sample ( kJ / kg ).arrow_forwardChapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... Scoresarrow_forwardmylabmastering.pearson.com Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... P Pearson MyLab and Mastering Scoresarrow_forwardanswer the fallowing Brake Specific Fuel Consumption - 0.3 kg/kwh, Mechanical Efficiency- 90% Calorific Value of Fuel -45 MJ/kg. Given these values, find the indicated power, indicated thermal efficiency and brake thermal efficiencyarrow_forwardProblem 6. The circular plate shown rotates about its vertical diameter. At the instant shown, the angular velocity ₁ of the plate is 10 rad/s and is decreasing at the rate of 25 rad/s². The disk lies in the XY plane and Point D of strap CD moves upward. The relative speed u of Point D of strap CD is 1.5 m/s and is decreasing at the rate of 3 m/s². Determine (a) the velocity of D, (b) the acceleration of D. Answers: =0.75 +1.299]-1.732k m/s a=-28.6 +3.03-10.67k m/s² 200 mm x Zarrow_forwardProblem 1. The flywheel A has an angular velocity o 5 rad/s. Link AB is connected via ball and socket joints to the flywheel at A and a slider at B. Find the angular velocity of link AB and the velocity of slider B at this instant. (Partial Answer: @ABN = -2î + 2.25; red Z -1.2 ft C -7 Y -1.5 ft- B 2.0 ftarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY