Chapter 4.4, Problem 43PPS

(a)

To determine

To calculate:Towrite an equation that represents the distance a butterfly will travel in $t$ days

Answer to Problem 43PPS

Equation that represents the distance a butterfly will travel in $t$ days is $d=50t$

Explanation of Solution

Given information:Every autumn, butterfly migrates up to $3000$ miles to California and Mexico where it hibernates until early spring. The butterfly travels on average $50$ miles per day.

Calculation:

Given thatthe butterfly travels on average $50$ miles per day.

Thus, the equation that represents the distance travelled by butterfly is

  $d=50t$

(b)

To determine

To calculate: Tocomplete the table

Answer to Problem 43PPS

Completed table is

Time (days)	1	2	3	4	5	6
Distance (miles)	50	100	150	200	250	300

Explanation of Solution

Given information:Equation that represents the distance travelled by butterfly is $d=50t$

Calculation:

Given that equation that represents the distance travelled by butterfly is follows:

  $50t=3000$

When $t=1$ , $d=50\left(1\right)=50$

When $t=2$ , $d=50\left(2\right)=100$

When $t=3$ , $d=50\left(3\right)=150$

When $t=4$ , $d=50\left(4\right)=200$

When $t=5$ , $d=50\left(5\right)=250$

When $t=6$ , $d=50\left(6\right)=300$

Hence, the completed table is as follows:

Time (days)	1	2	3	4	5	6
Distance (miles)	50	100	150	200	250	300

(c)

To determine

To calculate: Tograph the points the table on coordinate plane

Answer to Problem 43PPS

Points are graphed on coordinate plane

Explanation of Solution

Given information:Equation that represents the distance travelled by butterfly is $d=50t$

Calculation:

Table is given as

Time (days)	1	2	3	4	5	6
Distance (miles)	50	100	150	200	250	300

On plotting the points on coordinate plane,

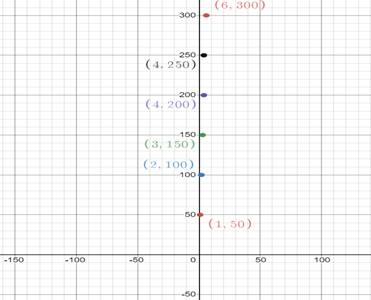
(d)

To determine

To calculate: Toestimate the number of days that butterfly will take to travel $450$ miles

Answer to Problem 43PPS

Butterfly will take $9$ daysto cover $450$ miles.

Explanation of Solution

Given information:Equation that represents the distance travelled by butterfly is $d=50t$

Calculation:

Table is given as

Time (days)	1	2	3	4	5	6
Distance (miles)	50	100	150	200	250	300

On plotting the points on coordinate plane,

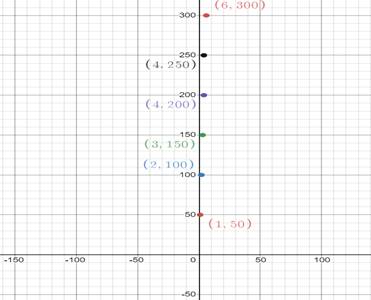
Hence number of days butterfly will take to cover $450$ miles is $9$ days.

(e)

To determine

To calculate: To estimate the number of days that butterfly will take to travel $2500$ miles

Answer to Problem 43PPS

Butterfly will take $50$ days to cover $2500$ miles.

Explanation of Solution

Given information:Equation that represents the distance travelled by butterfly is $d=50t$

Calculation:

Equation that represents the distance travelled by butterfly is $d=50t$

Here, $d=2500$

Substituting the value in above equation,

  $2500=50t$

On solving,

  $\begin{array}{l}50t=2500\\ t=\frac{2500}{50}\\ t=50\end{array}$

Hence number of days butterfly will take to cover $2500$ miles is $50$ days.