Chapter 4, Problem 41E

(a) Employ mesh analysis to determine the power dissipated by the 1 Ω resistor in the circuit represented schematically by Fig. 4.68. (b) Check your answer using nodal analysis.

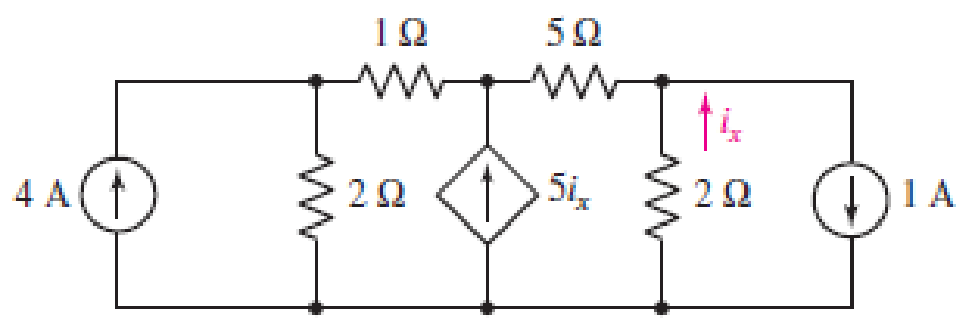
■ FIGURE 4.68

To determine

Employ mess analysis to find the power dissipated by the $1\Omega$ resistor.

Answer to Problem 41E

The power dissipated by the $1\Omega$ resistor is $1\text{ W}$.

Explanation of Solution

Calculation:

The circuit diagram is redrawn as shown in Figure 1,

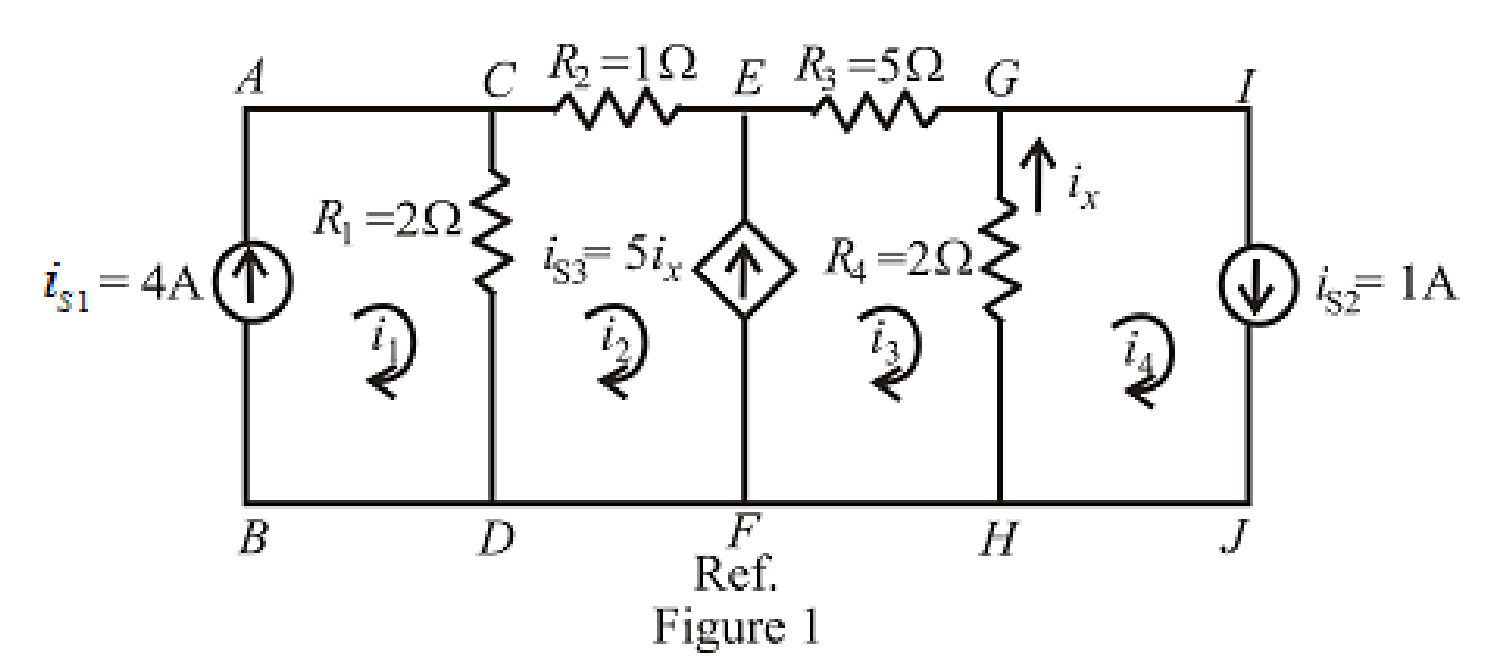
Refer to the redrawn Figure 1,

Apply KVL in the mesh $CEGHFDC$,

$(i_2-i_1)R_1+i_2{R}_2+i_3{R}_3+(i_3-i_4)R_4=0\text{ V}$ (1)

Here,

$i_1$ is the current flowing in the mesh $ACDBA$,

$i_2$ is the current flowing in the mesh $CEFDC$,

$i_3$ is the current flowing in the mesh $EGHFE$,

$i_4$ is the current flowing in the mesh $GIJHG$,

$R_1$ is the resistance across branch $CD$,

$R_2$ is the resistance across branch $CE$,

$R_3$ is the resistance across branch $EG$ and

$R_4$ is the resistance across branch $GH$.

The expression for the current flowing in the branch $EF$ is as follows,

$i_3-i_2=i_{S3}$ (2)

Here,

$i_{S3}$ is the current flowing in the branch $EF$.

The expression for the current flowing in the branch $GH$ is as follows,

$i_4-i_3=i_x$ (3)

Here,

$i_x$ is the current flowing in the branch $GH$.

The expression for the power dissipated by the $1\Omega$ resistor is as follows,

$p=i_2{R}_2$ (4)

Here,

$p$ is the power dissipated by the $1\Omega$ resistor.

Refer to the redrawn Figure 1,

Substitute $\text{4 A}$ for $i_1$, $\text{1 A}$ for $i_4$, $\text{2 }\Omega$ for $R_1$, $1\Omega$ for $R_2$, $\text{5 }\Omega$ for $R_3$ and $\text{2 }\Omega$ for $R_4$ in the equation (1),

$\left(\text{2 }\Omega \right)(i_2-\text{4 A})+\left(\text{1 }\Omega \right)i_2+\left(\text{5 }\Omega \right)i_3+\left(\text{2 }\Omega \right)(i_3-1\text{ A})=0\text{ V}$

$\left(\text{2 }\Omega \right)i_1-8\text{ V}+i_2+\left(\text{5 }\Omega \right)i_3+\left(\text{2 }\Omega \right)i_3-2\text{ V}=0\text{ V}$ (5)

Rearrange equation (5),

$3i_2+7i_3=10\text{ A}$ (6)

Substitute $5i_x$ for $i_{S3}$ in equation (2),

$i_3-i_2=5i_x$

Substitute $i_4-i_3$ for $i_x$ in the above equation,

$i_3-i_2=5\left(i_4-i_3\right)$

Substitute $\text{1 A}$ for $i_4$ in the above equation,

$\begin{array}{l}{i}_3-i_2=5\left(\text{1 A}-i_3\right)\\ i_3-i_2=\left(\text{5 A}-5i_3\right)\end{array}$

Rearrange the above equation for $i_2$,

$i_2=6i_3-5\text{ A}$ (7)

Substitute $6i_3-5\text{ A}$ for $i_2$ in equation (6),

$3\left(6i_3-5\text{ A}\right)+7i_3=10\text{ A}$

Rearrange for $i_3$,

$\begin{array}{c}\text{25}{i}_3=25\text{ A}\\ i_3=1\text{ A}\end{array}$

Substitute $1\text{ A}$ for $i_3$ in equation (7),

$\begin{array}{c}{i}_2=6\left(1\text{ A}\right)-5\text{ A}\\ =1\text{ A}\end{array}$

Substitute $1\text{ A}$ for $i_2$ and $1\Omega$ for $R_2$ in the equation (4),

$\begin{array}{c}p=\left(1\text{ A}\right)\left(1\Omega \right)\\ =1\text{ W}\end{array}$

Conclusion:

Thus, the power dissipated by the $1\Omega$ resistor is $1\text{ W}$.

To determine

Check the answer by nodal analysis.

Explanation of Solution

Formula used:

Refer to the redrawn Figure 1,

Apply KCL at node $C$.

$\frac{v_C-v_E}{R_2}+\frac{v_C}{R_1}=i_{S1}$ (8)

Here,

$v_E$ is the voltage at node $E$,

$v_C$ is the voltage at node $C$,

$R_1$ is the resistance across the branch $CD$,

$R_2$ is the resistance across the branch $CE$ and

$i_{S1}$ is the current through $4\text{ A}$ independent source.

Apply KCL at node $E$,

$\frac{v_E-v_C}{R_2}+\frac{v_E-v_G}{R_3}=i_{S3}$ (9)

Here,

$v_G$ is the voltage at node $G$,

$R_3$ is the resistance across the branch $EG$ and

$i_{S3}$ is the current through $5i_x$ dependent source

The expression for the current flowing in the branch $GH$ is as follows,

$i_x=\left(\frac{-v_G}{R_4}\right)$ (10)

Apply KCL at node $G$,

$\frac{v_G}{R_4}+\frac{v_G-v_E}{R_3}=-i_{S2}$ (11)

Here,

$R_4$ is the resistance across the branch $GH$ and

$i_{S2}$ is the current through $\text{1 A}$ independent source.

The expression for the power dissipated by the $1\Omega$ resistor is as follows,

$p_1=\frac{{\left(v_C-v_E\right)}^2}{R_2}$ (12)

Here,

$p_1$ is the power dissipated by the $1\Omega$ resistor.

Calculation:

Refer to the redrawn Figure 1,

Substitute $\text{2 }\Omega$ for $R_1$, $\text{1 }\Omega$ for $R_2$ and $\text{4 A}$ for $i_{S1}$ in equation (8),

$\frac{v_C-v_E}{\text{1 }\Omega }+\frac{v_C}{\text{2 }\Omega }=4\text{ A}$

$\frac{2v_C-2v_E+v_C}{\text{2 }\Omega }=4\text{ A}$ (13)

Substitute $\text{1 }\Omega$ for $R_2$, $\text{5 }\Omega$ for $R_3$ and ${\text{5i}}_x$ for $i_{S3}$ in the equation (9),

$\frac{v_E-v_C}{\text{1 }\Omega }+\frac{v_E-v_G}{\text{5 }\Omega }={\text{5i}}_x$

Substitute $\frac{-v_G}{R_4}$ for $i_x$ in the above equation.

$\frac{v_E-v_C}{\text{1 }\Omega }+\frac{v_E-v_G}{\text{5 }\Omega }=\text{5}\left(\frac{-v_G}{R_4}\right)$

Substitute $\text{2 }\Omega$ for $R_4$ in the above equation,

$\frac{v_E-v_C}{\text{1 }\Omega }+\frac{v_E-v_G}{\text{5 }\Omega }=\text{5}\left(\frac{-v_G}{\text{2 }\Omega }\right)$

$\frac{5v_E-5v_C+v_E-v_G}{\text{5 }\Omega }=\text{5}\left(\frac{-v_G}{\text{2 }\Omega }\right)$ (14)

Substitute $\text{5 }\Omega$ for $R_3$, $\text{2 }\Omega$ for $R_4$ and $\text{1 A}$ for $i_{S2}$ in equation (11),

$\frac{v_G}{\text{2 }\Omega }+\frac{v_G-v_E}{\text{5 }\Omega }=-\text{1 A}$

$\frac{5v_G+2v_G-2v_E}{\text{10 }\Omega }=-\text{1 A}$ (15)

Rearrange equation (13), (14) and (15),

$\begin{array}{c}3v_C-2v_E+0v_G=8\text{ V}\\ -5v_C+6v_E-11.5v_G=0\text{ V}\\ 0v_C-2v_E+7v_G=-10\text{ V}\end{array}$

The equations so formed can be written in matrix form as,

$\left(\begin{array}{ccc}3& -2& 0\\ -5& 6& -11.5\\ 0& -2& 7\end{array}\right)\left(\begin{array}{c}{v}_C\\ v_E\\ v_G\end{array}\right)=\left(\begin{array}{c}8\\ 0\\ -10\end{array}\right)$

Therefore, by Cramer’s rule,

The determinant of the coefficient matrix is as follows,

$\begin{array}{c}\Delta =\left|\begin{array}{ccc}3& -2& 0\\ -5& 6& -11.5\\ 0& -2& 7\end{array}\right|\\ =-13\end{array}$

The 1^st determinant is as follows,

$\begin{array}{c}{\Delta }_1=\left|\begin{array}{ccc}8& -2& 0\\ 0& 6& -11.5\\ 10& -2& 7\end{array}\right|\\ =-78\end{array}$

The 2^nd determinant is as follows,

$\begin{array}{c}{\Delta }_2=\left|\begin{array}{ccc}3& 8& 0\\ -5& 0& -11.5\\ 0& -10& 7\end{array}\right|\\ =-65\end{array}$

The 3^rd determinant is as follows,

$\begin{array}{c}{\Delta }_3=\left|\begin{array}{ccc}3& -2& 8\\ -5& 6& 0\\ 0& -2& -10\end{array}\right|\\ =0\end{array}$

Simplify for $v_C$,

$\begin{array}{c}{v}_C=\frac{{\Delta }_1}{\Delta }\\ =\frac{-78}{-13}\\ =6\text{ V}\end{array}$

Simplify for $v_E$,

$\begin{array}{c}{v}_E=\frac{{\Delta }_2}{\Delta }\\ =\frac{-65}{-13}\\ =5\text{ V}\end{array}$

Simplify for $v_G$,

$\begin{array}{c}{v}_G=\frac{{\Delta }_3}{\Delta }\\ =\frac{0}{-13}\\ =0\text{ V}\end{array}$

Substitute $6\text{ V}$ for $v_C$ and $5\text{ V}$ for $v_E$ in equation (12),

$\begin{array}{c}{p}_1=\frac{{\left(6\text{ V}-5\text{ V}\right)}^2}{1\Omega }\\ =\frac{{\left(\text{1 V}\right)}^2}{1\Omega }\\ =1\text{ W}\end{array}$

So, the power dissipated by the $1\Omega$ resistor is same by both mesh analysis and nodal analysis.

Conclusion:

Thus, the answer is checked by using nodal analysis.