Chapter 4, Problem 36E

To determine

Find the power dissipated by each resistor in the circuit.

Answer to Problem 36E

The power dissipated by $1\Omega$ resistor is $703.9\text{ mW}$, by $9\Omega$ resistor is $416.2\mu \text{W}$, by $5\Omega$ resistor is $3.46\text{ W}$, by $6\Omega$ resistor is $135.4\text{ mW}$ and by $7\Omega$ resistor is $172.5\text{ mW}$.

Explanation of Solution

Calculation:

The circuit diagram is redrawn as shown in Figure 1.

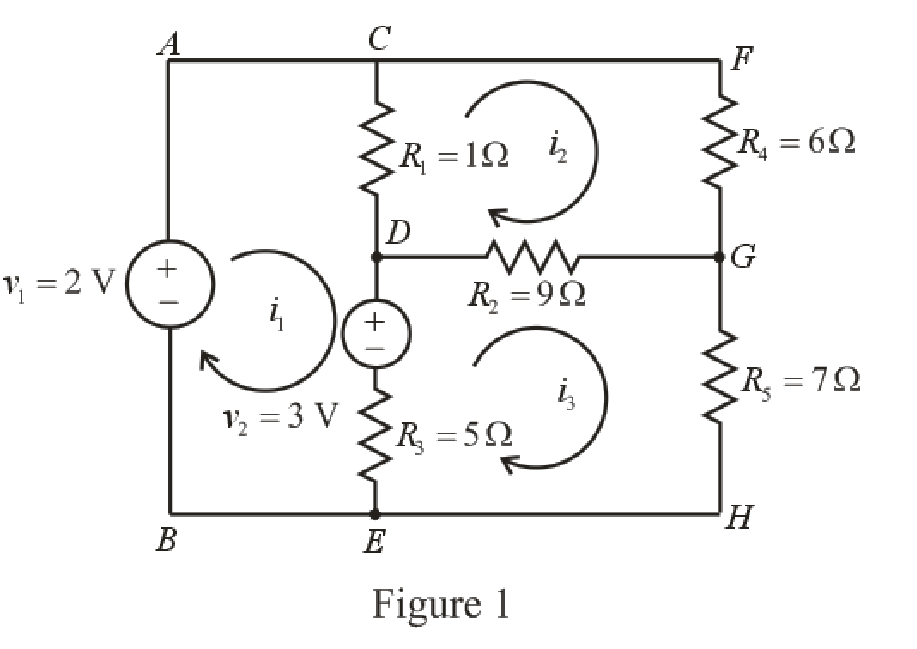
Refer to the redrawn Figure 1

Apply KVL in the mesh $ACDEA$.

$v_1=(i_1-i_2)R_1-v_2+(i_1-i_3)R_3$ (1)

Here,

$v_1$ is the voltage of $1\text{ V}$ independent source,

$v_2$ is the voltage of $3\text{ V}$ independent source,

$i_1$ is the current flowing in the mesh $ACDEA$,

$i_2$ is the current flowing in the mesh $CFGDC$,

$i_3$ is the current flowing in the mesh $DGHED$,

$R_1$ is the resistance across branch $CD$ and

$R_3$ is the resistance across branch $DE$.

Apply KVL in the mesh $CFGDC$.

$(i_2-i_1)R_1+i_2{R}_4+(i_2-i_3)R_2=0$ (2)

Here,

$R_2$ is the resistance across branch $DG$,

$R_4$ is the resistance across branch $FG$.

Apply KVL in the mesh $DGHED$.

$(i_3-i_1)R_3+v_2+(i_3-i_2)R_2+i_3{R}_5=0$ (3)

Here,

$R_5$ is the resistance across branch $GH$.

The expression for the power dissipated by the resistor is as follows.

$p=i^{2}R$ (4)

Here,

$i$ is the current flowing through resistor and

$R$ is the resistor.

The current flowing through the $R_1$ resistor is as follows.

$i_{1\Omega }=(i_1-i_2)$ (5)

Here,

$i_{1\Omega }$ is the current flowing through $1\Omega$ resistor.

The current flowing through the $R_2$ resistor is as follows.

$i_{\text{9 }\Omega }=(i_3-i_2)$ (6)

Here,

$i_{\text{9 }\Omega }$ is the current flowing through $9\Omega$ resistor.

The current flowing through the $R_3$ resistor is as follows.

$i_{\text{5 }\Omega }=(i_1-i_3)$ (7)

Here,

$i_{\text{5 }\Omega }$ is the current flowing through $5\Omega$ resistor.

Refer to the redrawn Figure 1.

Substitute $\text{2 V}$ for $v_1$, $\text{1 }\Omega$ for $R_1$, $5\Omega$ for $R_3$ and $3\text{ V}$ for $v_2$ in the equation (1).

$\text{2 V}=\left(\text{1 }\Omega \right)(i_1-i_2)-3\text{ V}+\left(5\Omega \right)(i_1-i_3)$ (8)

Substitute $\text{1 }\Omega$ for $R_1$, $9\Omega$ for $R_2$ and $6\Omega$ for $R_4$ in the equation (2).

$\left(\text{1 }\Omega \right)(i_2-i_1)+\left(\text{6 }\Omega \right)i_2+\left(\text{9 }\Omega \right)(i_2-i_3)=0$ (9)

Substitute $5\Omega$ for $R_3$, $9\Omega$ for $R_2$, $\text{7 }\Omega$ for $R_5$ and $3\text{ V}$ for $v_2$ in the equation (3).

$\left(5\Omega \right)(i_3-i_1)+3\text{ V}+\left(9\Omega \right)(i_3-i_2)+\left(7\Omega \right)i_3=0$ (10)

Rearrange the equation (8), (9) and (10).

$\begin{array}{l}6i_1-i_2-5i_3=5\text{ V}\\ -i_1+16i_2-9i_3=0\text{ V}\\ 5i_1+9i_2-21i_3=3\text{ V}\end{array}$

The equations so formed can be written in matrix form as,

$\left(\begin{array}{ccc}6& -1& -5\\ -1& 16& -9\\ 5& 9& -21\end{array}\right)\left(\begin{array}{c}{i}_1\\ i_2\\ i_3\end{array}\right)=\left(\begin{array}{c}5\\ 0\\ 3\end{array}\right)$

Therefore, by Cramer’s rule,

The determinant of coefficient matrix is as follows,

$\begin{array}{c}\Delta =\left|\begin{array}{ccc}6& -1& -5\\ -1& 16& -9\\ 5& 9& -21\end{array}\right|\\ =-1019\end{array}$

The 1^st determinant is as follows.

$\begin{array}{c}{\Delta }_{i_1}=\left|\begin{array}{ccc}5& -1& -5\\ 0& 16& -9\\ 3& 9& -21\end{array}\right|\\ =-1008\end{array}$

The 2^nd determinant is as follows.

$\begin{array}{c}{\Delta }_{i_2}=\left|\begin{array}{ccc}6& 5& -5\\ -1& 0& -9\\ 5& 3& -21\end{array}\right|\\ =-153\end{array}$

The 3rd determinant is as follows.

$\begin{array}{c}{\Delta }_{i_3}=\left|\begin{array}{ccc}6& -1& 5\\ -1& 16& 0\\ 5& 9& 3\end{array}\right|\\ =-160\end{array}$

Simplify for $i_1$.

$\begin{array}{c}{i}_1=\frac{{\Delta }_{i_1}}{\Delta }\\ =\frac{-1008}{-1019}\text{ A}\\ =0.9892\text{ A}\\ =989.2\text{ mA }\left\{\because 1\text{ A}={10}^3\text{ mA}\right\}\end{array}$

Simplify for $i_2$.

$\begin{array}{c}{i}_2=\frac{{\Delta }_{i_2}}{\Delta }\\ =\frac{-153}{-1019}\text{ A}\\ =0.1501\text{ A}\\ =150.1\text{ mA }\left\{\because 1\text{ A}={10}^3\text{ mA}\right\}\end{array}$

Simplify for $i_3$.

$\begin{array}{c}{i}_3=\frac{{\Delta }_{i_3}}{\Delta }\\ =\frac{-160}{-1019}\text{ A}\\ =0.1570\text{ A}\\ =157.0\text{ mA }\left\{\because 1\text{ A}={10}^3\text{ mA}\right\}\end{array}$

Substitute $989.2\text{ mA}$ for $i_1$ and $150.2\text{ mA}$ for $i_2$ in equation (5).

$\begin{array}{c}{i}_{1\Omega }=(989.2\text{ mA}-150.2\text{ mA})\\ =839\text{ mA}\end{array}$

Substitute $839.1\text{ mA}$ for $i$ and $\text{1 }\Omega$ for $R$ in equation (4).

$\begin{array}{c}p=\left({\left(839\text{ mA}\right)}^2\times \text{1 }\Omega \right)\\ =703921\mu \text{W}\\ =703.9\text{ mW }\left\{\because 1\mu \text{W}={10}^{-3}\text{ mW}\right\}\end{array}$

Substitute $157.0\text{ mA}$ for $i_3$ and $150.2\text{ mA}$ for $i_2$ in equation (6).

$\begin{array}{c}{i}_{\text{9 }\Omega }=(157.0\text{ mA}-150.2\text{ mA})\\ =6.8\text{ mA }\end{array}$

Substitute $6.8\text{ mA}$ for $i$ and $\text{9 }\Omega$ for $R$ in equation (4).

$\begin{array}{c}p=\left({\left(6.8\text{ mA}\right)}^2\times \text{9 }\Omega \right)\\ =416.2\text{ μW}\end{array}$

Substitute $157.0\text{ mA}$ for $i_3$ and $989.2\text{ mA}$ for $i_1$ in equation (7).

$\begin{array}{c}{i}_{\text{5 }\Omega }=(989.2\text{ mA}-157.0\text{ mA)}\\ =832.2\text{ mA }\end{array}$

Substitute $832.2\text{ mA}$ for $i$ and $\text{5 }\Omega$ for $R$ in equation (4).

$\begin{array}{c}p=\left({\left(832.2\text{ mA}\right)}^2\times \text{5 }\Omega \right)\\ =3462784.2\mu \text{W}\\ =3.46\text{ W }\left\{\because 1\mu \text{W}={10}^{-6}\text{ W}\right\}\end{array}$

Substitute $150.2\text{ mA}$ for $i$ and $\text{6 }\Omega$ for $R$ in equation (4).

$\begin{array}{c}p=\left({\left(150.2\text{ mA}\right)}^2\times \text{6 }\Omega \right)\\ =135360.24\mu \text{W}\\ =135.4\text{ mW }\left\{\because 1\mu \text{W}={10}^{-3}\text{ mW}\right\}\end{array}$

Substitute $157.0\text{ mA}$ for $i$ and $\text{7 }\Omega$ for $R$ in equation (4).

$\begin{array}{c}p=\left({\left(157.0\text{ mA}\right)}^2\times 7\Omega \right)\\ =172543\mu \text{W}\\ =172.5\text{ mW }\left\{\because 1\mu \text{W}={10}^{-3}\text{ mW}\right\}\end{array}$

Conclusion:

Thus, the power dissipated by $1\Omega$ resistor is $703.9\text{ mW}$, by $9\Omega$ resistor is $416.2\mu \text{W}$, by $5\Omega$ resistor is $3.46\text{ W}$, by $6\Omega$ resistor is $135.4\text{ mW}$ and by $7\Omega$ resistor is $172.5\text{ mW}$.