Algebra 2
1st Edition
ISBN: 9780078884825
Author: McGraw-Hill/Glencoe
Publisher: Glencoe/McGraw-Hill School Pub Co
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 3.3, Problem 2BCYP
To determine
To find: The solution of the given system of inequalities.
Expert Solution & Answer
Answer to Problem 2BCYP
The solution of the given system of inequalities is the common region of red and blue.
Explanation of Solution
Given information:
The given system of inequalities is,
The given system of inequalities is,
Consider the graph of the given inequalities as,
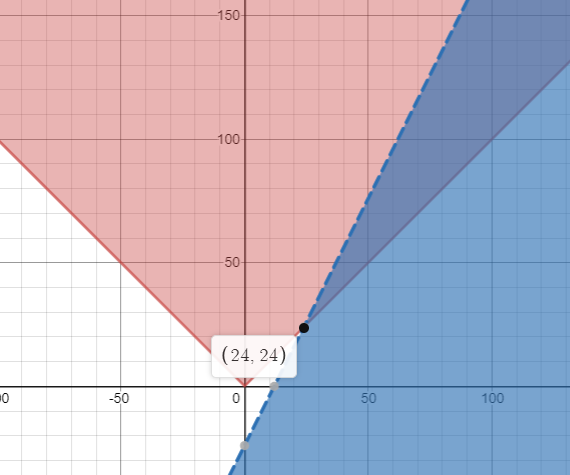
Thus, the solution of the given system of inequalities is the common region of red and blue.
Chapter 3 Solutions
Algebra 2
Ch. 3.1 - Prob. 1ACYPCh. 3.1 - Prob. 1BCYPCh. 3.1 - Prob. 2ACYPCh. 3.1 - Prob. 2BCYPCh. 3.1 - Prob. 3CYPCh. 3.1 - Prob. 4ACYPCh. 3.1 - Prob. 4BCYPCh. 3.1 - Prob. 4CCYPCh. 3.1 - Prob. 4DCYPCh. 3.1 - Prob. 1CYU
Ch. 3.1 - Prob. 2CYUCh. 3.1 - Prob. 3CYUCh. 3.1 - Prob. 4CYUCh. 3.1 - Prob. 5CYUCh. 3.1 - Prob. 6CYUCh. 3.1 - Prob. 7CYUCh. 3.1 - Prob. 8CYUCh. 3.1 - Prob. 9CYUCh. 3.1 - Prob. 10CYUCh. 3.1 - Prob. 11CYUCh. 3.1 - Prob. 12CYUCh. 3.1 - Prob. 13PPSCh. 3.1 - Prob. 14PPSCh. 3.1 - Prob. 15PPSCh. 3.1 - Prob. 16PPSCh. 3.1 - Prob. 17PPSCh. 3.1 - Prob. 18PPSCh. 3.1 - Prob. 19PPSCh. 3.1 - Prob. 20PPSCh. 3.1 - Prob. 21PPSCh. 3.1 - Prob. 22PPSCh. 3.1 - Prob. 23PPSCh. 3.1 - Prob. 24PPSCh. 3.1 - Prob. 25PPSCh. 3.1 - Prob. 26PPSCh. 3.1 - Prob. 27PPSCh. 3.1 - Prob. 28PPSCh. 3.1 - Prob. 29PPSCh. 3.1 - Prob. 30PPSCh. 3.1 - Prob. 31PPSCh. 3.1 - Prob. 32PPSCh. 3.1 - Prob. 33PPSCh. 3.1 - Prob. 34PPSCh. 3.1 - Prob. 35PPSCh. 3.1 - Prob. 36PPSCh. 3.1 - Prob. 37PPSCh. 3.1 - Prob. 38PPSCh. 3.1 - Prob. 39PPSCh. 3.1 - Prob. 40PPSCh. 3.1 - Prob. 41PPSCh. 3.1 - Prob. 42HPCh. 3.1 - Prob. 43HPCh. 3.1 - Prob. 44HPCh. 3.1 - Prob. 45HPCh. 3.1 - Prob. 46HPCh. 3.1 - Prob. 47HPCh. 3.1 - Prob. 48HPCh. 3.1 - Prob. 49HPCh. 3.1 - Prob. 50HPCh. 3.1 - Prob. 51STPCh. 3.1 - Prob. 52STPCh. 3.1 - Prob. 53STPCh. 3.1 - Prob. 54STPCh. 3.1 - Prob. 55STPCh. 3.1 - Prob. 56STPCh. 3.1 - Prob. 57STPCh. 3.1 - Prob. 58STPCh. 3.1 - Prob. 59STPCh. 3.1 - Prob. 60STPCh. 3.1 - Prob. 61SCh. 3.1 - Prob. 62SCh. 3.1 - Prob. 63SCh. 3.1 - Prob. 64SCh. 3.1 - Prob. 65SCh. 3.1 - Prob. 66SCh. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10ECh. 3.2 - Prob. 1ACYPCh. 3.2 - Prob. 1BCYPCh. 3.2 - Prob. 1CCYPCh. 3.2 - Prob. 2ACYPCh. 3.2 - Prob. 2BCYPCh. 3.2 - Prob. 2CCYPCh. 3.2 - Prob. 3CYPCh. 3.2 - Prob. 4ACYPCh. 3.2 - Prob. 4BCYPCh. 3.2 - Prob. 1CYUCh. 3.2 - Prob. 2CYUCh. 3.2 - Prob. 3CYUCh. 3.2 - Prob. 4CYUCh. 3.2 - Prob. 5CYUCh. 3.2 - Prob. 6CYUCh. 3.2 - Prob. 7CYUCh. 3.2 - Prob. 8CYUCh. 3.2 - Prob. 9CYUCh. 3.2 - Prob. 10CYUCh. 3.2 - Prob. 11CYUCh. 3.2 - Prob. 12CYUCh. 3.2 - Prob. 13CYUCh. 3.2 - Prob. 14CYUCh. 3.2 - Prob. 15PPSCh. 3.2 - Prob. 16PPSCh. 3.2 - Prob. 17PPSCh. 3.2 - Prob. 18PPSCh. 3.2 - Prob. 19PPSCh. 3.2 - Prob. 20PPSCh. 3.2 - Prob. 21PPSCh. 3.2 - Prob. 22PPSCh. 3.2 - Prob. 23PPSCh. 3.2 - Prob. 24PPSCh. 3.2 - Prob. 25PPSCh. 3.2 - Prob. 26PPSCh. 3.2 - Prob. 27PPSCh. 3.2 - Prob. 28PPSCh. 3.2 - Prob. 29PPSCh. 3.2 - Prob. 30PPSCh. 3.2 - Prob. 31PPSCh. 3.2 - Prob. 32PPSCh. 3.2 - Prob. 33PPSCh. 3.2 - Prob. 34PPSCh. 3.2 - Prob. 35PPSCh. 3.2 - Prob. 36PPSCh. 3.2 - Prob. 37PPSCh. 3.2 - Prob. 38PPSCh. 3.2 - Prob. 39PPSCh. 3.2 - Prob. 40PPSCh. 3.2 - Prob. 41PPSCh. 3.2 - Prob. 42PPSCh. 3.2 - Prob. 43PPSCh. 3.2 - Prob. 44PPSCh. 3.2 - Prob. 45PPSCh. 3.2 - Prob. 46PPSCh. 3.2 - Prob. 47PPSCh. 3.2 - Prob. 48PPSCh. 3.2 - Prob. 49PPSCh. 3.2 - Prob. 50PPSCh. 3.2 - Prob. 51PPSCh. 3.2 - Prob. 52PPSCh. 3.2 - Prob. 53PPSCh. 3.2 - Prob. 54PPSCh. 3.2 - Prob. 55PPSCh. 3.2 - Prob. 56PPSCh. 3.2 - Prob. 57PPSCh. 3.2 - Prob. 58PPSCh. 3.2 - Prob. 59PPSCh. 3.2 - Prob. 60PPSCh. 3.2 - Prob. 61PPSCh. 3.2 - Prob. 62PPSCh. 3.2 - Prob. 63PPSCh. 3.2 - Prob. 64HPCh. 3.2 - Prob. 65HPCh. 3.2 - Prob. 66HPCh. 3.2 - Prob. 67HPCh. 3.2 - Prob. 68HPCh. 3.2 - Prob. 69HPCh. 3.2 - Prob. 70HPCh. 3.2 - Prob. 71HPCh. 3.2 - Prob. 72HPCh. 3.2 - Prob. 73STPCh. 3.2 - Prob. 74STPCh. 3.2 - Prob. 75STPCh. 3.2 - Prob. 76STPCh. 3.2 - Prob. 77STPCh. 3.2 - Prob. 78STPCh. 3.2 - Prob. 79STPCh. 3.2 - Prob. 80STPCh. 3.2 - Prob. 81SCh. 3.2 - Prob. 82SCh. 3.2 - Prob. 83SCh. 3.3 - Prob. 1ACYPCh. 3.3 - Prob. 1BCYPCh. 3.3 - Prob. 2ACYPCh. 3.3 - Prob. 2BCYPCh. 3.3 - Prob. 3CYPCh. 3.3 - Prob. 4ACYPCh. 3.3 - Prob. 4BCYPCh. 3.3 - Prob. 1CYUCh. 3.3 - Prob. 2CYUCh. 3.3 - Prob. 3CYUCh. 3.3 - Prob. 4CYUCh. 3.3 - Prob. 5CYUCh. 3.3 - Prob. 6CYUCh. 3.3 - Prob. 7PPSCh. 3.3 - Prob. 8PPSCh. 3.3 - Prob. 9PPSCh. 3.3 - Prob. 10PPSCh. 3.3 - Prob. 11PPSCh. 3.3 - Prob. 12PPSCh. 3.3 - Prob. 13PPSCh. 3.3 - Prob. 14PPSCh. 3.3 - Prob. 15PPSCh. 3.3 - Prob. 16PPSCh. 3.3 - Prob. 17PPSCh. 3.3 - Prob. 18PPSCh. 3.3 - Prob. 19PPSCh. 3.3 - Prob. 20PPSCh. 3.3 - Prob. 21PPSCh. 3.3 - Prob. 22PPSCh. 3.3 - Prob. 23PPSCh. 3.3 - Prob. 24PPSCh. 3.3 - Prob. 25PPSCh. 3.3 - Prob. 26PPSCh. 3.3 - Prob. 27PPSCh. 3.3 - Prob. 28PPSCh. 3.3 - Prob. 29PPSCh. 3.3 - Prob. 30PPSCh. 3.3 - Prob. 31PPSCh. 3.3 - Prob. 32PPSCh. 3.3 - Prob. 33PPSCh. 3.3 - Prob. 34PPSCh. 3.3 - Prob. 35PPSCh. 3.3 - Prob. 36PPSCh. 3.3 - Prob. 37PPSCh. 3.3 - Prob. 38PPSCh. 3.3 - Prob. 39PPSCh. 3.3 - Prob. 40PPSCh. 3.3 - Prob. 41PPSCh. 3.3 - Prob. 42PPSCh. 3.3 - Prob. 43PPSCh. 3.3 - Prob. 44PPSCh. 3.3 - Prob. 45HPCh. 3.3 - Prob. 46HPCh. 3.3 - Prob. 47HPCh. 3.3 - Prob. 48HPCh. 3.3 - Prob. 49HPCh. 3.3 - Prob. 50HPCh. 3.3 - Prob. 51HPCh. 3.3 - Prob. 52HPCh. 3.3 - Prob. 53HPCh. 3.3 - Prob. 54HPCh. 3.3 - Prob. 55STPCh. 3.3 - Prob. 56STPCh. 3.3 - Prob. 57STPCh. 3.3 - Prob. 58STPCh. 3.3 - Prob. 59STPCh. 3.3 - Prob. 60STPCh. 3.3 - Prob. 61STPCh. 3.3 - Prob. 62STPCh. 3.3 - Prob. 63SCh. 3.3 - Prob. 64SCh. 3.3 - Prob. 65SCh. 3.3 - Prob. 66SCh. 3.3 - Prob. 67SCh. 3.3 - Prob. 68SCh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.4 - Prob. 1ACYPCh. 3.4 - Prob. 1BCYPCh. 3.4 - Prob. 2ACYPCh. 3.4 - Prob. 2BCYPCh. 3.4 - Prob. 3CYPCh. 3.4 - Prob. 1CYUCh. 3.4 - Prob. 2CYUCh. 3.4 - Prob. 3CYUCh. 3.4 - Prob. 4CYUCh. 3.4 - Prob. 5CYUCh. 3.4 - Prob. 6CYUCh. 3.4 - Prob. 7CYUCh. 3.4 - Prob. 8PPSCh. 3.4 - Prob. 9PPSCh. 3.4 - Prob. 10PPSCh. 3.4 - Prob. 11PPSCh. 3.4 - Prob. 12PPSCh. 3.4 - Prob. 13PPSCh. 3.4 - Prob. 14PPSCh. 3.4 - Prob. 15PPSCh. 3.4 - Prob. 16PPSCh. 3.4 - Prob. 17PPSCh. 3.4 - Prob. 18PPSCh. 3.4 - Prob. 19PPSCh. 3.4 - Prob. 20PPSCh. 3.4 - Prob. 21PPSCh. 3.4 - Prob. 22PPSCh. 3.4 - Prob. 23PPSCh. 3.4 - Prob. 24PPSCh. 3.4 - Prob. 25PPSCh. 3.4 - Prob. 26PPSCh. 3.4 - Prob. 27PPSCh. 3.4 - Prob. 28PPSCh. 3.4 - Prob. 29PPSCh. 3.4 - Prob. 30HPCh. 3.4 - Prob. 31HPCh. 3.4 - Prob. 32HPCh. 3.4 - Prob. 33HPCh. 3.4 - Prob. 34HPCh. 3.4 - Prob. 35HPCh. 3.4 - Prob. 36HPCh. 3.4 - Prob. 37HPCh. 3.4 - Prob. 38STPCh. 3.4 - Prob. 39STPCh. 3.4 - Prob. 40STPCh. 3.4 - Prob. 41STPCh. 3.4 - Prob. 42STPCh. 3.4 - Prob. 43STPCh. 3.4 - Prob. 44STPCh. 3.4 - Prob. 45STPCh. 3.4 - Prob. 46STPCh. 3.4 - Prob. 47STPCh. 3.4 - Prob. 48STPCh. 3.4 - Prob. 49STPCh. 3.4 - Prob. 50SCh. 3.4 - Prob. 51SCh. 3.4 - Prob. 52SCh. 3.4 - Prob. 53SCh. 3.4 - Prob. 54SCh. 3.4 - Prob. 55SCh. 3.5 - Prob. 1ACYPCh. 3.5 - Prob. 1BCYPCh. 3.5 - Prob. 2ACYPCh. 3.5 - Prob. 2BCYPCh. 3.5 - Prob. 3CYPCh. 3.5 - Prob. 1CYUCh. 3.5 - Prob. 2CYUCh. 3.5 - Prob. 3CYUCh. 3.5 - Prob. 4CYUCh. 3.5 - Prob. 5CYUCh. 3.5 - Prob. 6CYUCh. 3.5 - Prob. 7CYUCh. 3.5 - Prob. 8PPSCh. 3.5 - Prob. 9PPSCh. 3.5 - Prob. 10PPSCh. 3.5 - Prob. 11PPSCh. 3.5 - Prob. 12PPSCh. 3.5 - Prob. 13PPSCh. 3.5 - Prob. 14PPSCh. 3.5 - Prob. 15PPSCh. 3.5 - Prob. 16PPSCh. 3.5 - Prob. 17PPSCh. 3.5 - Prob. 18PPSCh. 3.5 - Prob. 19PPSCh. 3.5 - Prob. 20PPSCh. 3.5 - Prob. 21PPSCh. 3.5 - Prob. 22PPSCh. 3.5 - Prob. 23PPSCh. 3.5 - Prob. 24HPCh. 3.5 - Prob. 25HPCh. 3.5 - Prob. 26HPCh. 3.5 - Prob. 27HPCh. 3.5 - Prob. 28HPCh. 3.5 - Prob. 29HPCh. 3.5 - Prob. 30HPCh. 3.5 - Prob. 31HPCh. 3.5 - Prob. 32HPCh. 3.5 - Prob. 33HPCh. 3.5 - Prob. 34STPCh. 3.5 - Prob. 35STPCh. 3.5 - Prob. 36STPCh. 3.5 - Prob. 37STPCh. 3.5 - Prob. 38STPCh. 3.5 - Prob. 39SCh. 3.5 - Prob. 40SCh. 3.5 - Prob. 41SCh. 3.5 - Prob. 42SCh. 3 - Prob. 1QCCh. 3 - Prob. 2QCCh. 3 - Prob. 3QCCh. 3 - Prob. 4QCCh. 3 - Prob. 5QCCh. 3 - Prob. 6QCCh. 3 - Prob. 7QCCh. 3 - Prob. 8QCCh. 3 - Prob. 9QCCh. 3 - Prob. 10QCCh. 3 - Prob. 11QCCh. 3 - Prob. 12QCCh. 3 - Prob. 13QCCh. 3 - Prob. 14QCCh. 3 - Prob. 1MCQCh. 3 - Prob. 2MCQCh. 3 - Prob. 3MCQCh. 3 - Prob. 4MCQCh. 3 - Prob. 5MCQCh. 3 - Prob. 6MCQCh. 3 - Prob. 7MCQCh. 3 - Prob. 8MCQCh. 3 - Prob. 9MCQCh. 3 - Prob. 10MCQCh. 3 - Prob. 11MCQCh. 3 - Prob. 12MCQCh. 3 - Prob. 13MCQCh. 3 - Prob. 14MCQCh. 3 - Prob. 15MCQCh. 3 - Prob. 16MCQCh. 3 - Prob. 17MCQCh. 3 - Prob. 18MCQCh. 3 - Prob. 19MCQCh. 3 - Prob. 20MCQCh. 3 - Prob. 21MCQCh. 3 - Prob. 22MCQCh. 3 - Prob. 1SGRCh. 3 - Prob. 2SGRCh. 3 - Prob. 3SGRCh. 3 - Prob. 4SGRCh. 3 - Prob. 5SGRCh. 3 - Prob. 6SGRCh. 3 - Prob. 7SGRCh. 3 - Prob. 8SGRCh. 3 - Prob. 9SGRCh. 3 - Prob. 10SGRCh. 3 - Prob. 11SGRCh. 3 - Prob. 12SGRCh. 3 - Prob. 13SGRCh. 3 - Prob. 14SGRCh. 3 - Prob. 15SGRCh. 3 - Prob. 16SGRCh. 3 - Prob. 17SGRCh. 3 - Prob. 18SGRCh. 3 - Prob. 19SGRCh. 3 - Prob. 20SGRCh. 3 - Prob. 21SGRCh. 3 - Prob. 22SGRCh. 3 - Prob. 23SGRCh. 3 - Prob. 24SGRCh. 3 - Prob. 25SGRCh. 3 - Prob. 26SGRCh. 3 - Prob. 27SGRCh. 3 - Prob. 28SGRCh. 3 - Prob. 29SGRCh. 3 - Prob. 30SGRCh. 3 - Prob. 1PTCh. 3 - Prob. 2PTCh. 3 - Prob. 3PTCh. 3 - Prob. 4PTCh. 3 - Prob. 5PTCh. 3 - Prob. 6PTCh. 3 - Prob. 7PTCh. 3 - Prob. 8PTCh. 3 - Prob. 9PTCh. 3 - Prob. 10PTCh. 3 - Prob. 11PTCh. 3 - Prob. 12PTCh. 3 - Prob. 13PTCh. 3 - Prob. 14PTCh. 3 - Prob. 15PTCh. 3 - Prob. 16PTCh. 3 - Prob. 17PTCh. 3 - Prob. 18PTCh. 3 - Prob. 19PTCh. 3 - Prob. 1ECh. 3 - Prob. 2ECh. 3 - Prob. 3ECh. 3 - Prob. 4ECh. 3 - Prob. 1STPCh. 3 - Prob. 2STPCh. 3 - Prob. 3STPCh. 3 - Prob. 4STPCh. 3 - Prob. 5STPCh. 3 - Prob. 6STPCh. 3 - Prob. 7STPCh. 3 - Prob. 8STPCh. 3 - Prob. 9STPCh. 3 - Prob. 10STPCh. 3 - Prob. 11STPCh. 3 - Prob. 12STPCh. 3 - Prob. 13STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
Rational functions Determine limxf(x) and limxf(x) for the following rational functions. Then give the horizont...
Calculus: Early Transcendentals (2nd Edition)
ASSESSMENT Find the first five terms in sequences with the following nth terms. a. n2+2 b. 5n+1 c. 10n1 d. 3n2 ...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
A linear equation is solved by using the intersection of graphs method. Find the solution by interpreting the g...
College Algebra with Modeling & Visualization (5th Edition)
A child has 12 blocks, of which 6 are black, 4 are red, 1 is white, and 1 is blue. If the child puts the blocks...
A First Course in Probability (10th Edition)
IQ Scores. In Exercises 5–8, find the area of the shaded region. The graphs depict IQ scores of adults, and tho...
Elementary Statistics (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Let & be linear map from as Pacex into aspace and {X1, X2, – 1— x3 basis for x show that f a one-to-one isf {f(x1), f (xx); — F (Kn) } linearly independent. மம் let M be a Proper sub space of aspace X then M is ahyper space iff for any text&M X=. C) let X be a linear space and fe X1{0} Show that is bjective or not and why? ***********arrow_forwardQ₁/(a) Let S and T be subsets of a vector space X over a field F such that SCT,show that whether (1) if S generate X then T generate X or not. (2) if T generate X then S generate X or not. (b) Let X be a vector space over a field F and A,B are subsets of X such that A is convex set and B is affine set, show that whether AnB is convex set or not, and if f be a function from X into a space Y then f(B) is an affine set or not. /(a) Let M and N be two hyperspaces of a space X write a condition to prove MUN is a hyperspace of X and condition to get that MUN is not hyperspace of X. Write with prove application n Panach theoremarrow_forwardMatch the division problem on the left with the correct quotient on the left. Note that the denominators of the reminders are omitted and replaced with R. 1) (k3-10k²+k+1) ÷ (k − 1) 2) (k4-4k-28k45k+26)+(k+7) 3) (20k+222-7k+7)+(5k-2) 4) (3+63-15k +32k-25)+(k+4) 5) (317k 13) ÷ (k+4) - 6) (k-k+8k+5)+(k+1) 7) (4-12k+6) + (k-3) 8) (3k+4k3 + 15k + 10) ÷ (3k+4) A) 3k3-6k29k - 4 B) 4k2 + 6 R 7 C)²-9k-8- R D) 4k2+6x+1+ E) 10 Elk³-5-12 R 9 F) k² - 4k R 9 R G) k3-3k2-7k+4 H) k³-k²+8 - 3 R - R 9 Rarrow_forward
- Answer choices are: 35 7 -324 4 -9 19494 5 684 3 -17 -3 20 81 15 8 -1 185193arrow_forwardlearn.edgenuity : C&C VIP Unit Test Unit Test Review Active 1 2 3 4 Which statement is true about the graph of the equation y = csc¯¹(x)? There is a horizontal asymptote at y = 0. उद There is a horizontal asymptote at y = 2. There is a vertical asymptote at x = 0. O There is a vertical asymptote at x=- R Mark this and return C Save and Exit emiarrow_forwardے ملزمة احمد Q (a) Let f be a linear map from a space X into a space Y and (X1,X2,...,xn) basis for X, show that fis one-to- one iff (f(x1),f(x2),...,f(x) } linearly independent. (b) Let X= {ao+ax₁+a2x2+...+anxn, a;ER} be a vector space over R, write with prove a hyperspace and a hyperplane of X. مبر خد احمد Q₂ (a) Let M be a subspace of a vector space X, and A= {fex/ f(x)=0, x E M ), show that whether A is convex set or not, affine set or not. Write with prove an application of Hahn-Banach theorem. Show that every singleton set in a normed space X is closed and any finite set in X is closed (14M)arrow_forward
- Let M be a proper subspace of a finite dimension vector space X over a field F show that whether: (1) If S is a base for M then S base for X or not, (2) If T base for X then base for M or not. (b) Let X-P₂(x) be a vector space over polynomials a field of real numbers R, write with L prove convex subset of X and hyperspace of X. Q₂/ (a) Let X-R³ be a vector space over a over a field of real numbers R and A=((a,b,o), a,bE R), A is a subspace of X, let g be a function from A into R such that gla,b,o)-a, gEA, find fe X such that g(t)=f(t), tEA. (b) Let M be a non-empty subset of a space X, show that M is a hyperplane of X iff there Xiff there exists fE X/10) and tE F such that M=(xE X/ f(x)=t). (c) Show that the relation equivalent is an equivalence relation on set of norms on a space X.arrow_forwardQ/(a)Let X be a finite dimension vector space over a field F and S₁,S2CX such that S₁SS2. Show that whether (1) if S, is a base for X then base for X or not (2) if S2 is a base for X then S, is a base for X or not (b) Show that every subspace of vector space is convex and affine set but the conevrse need not to be true. allet M be a non-empty subset of a vector space X over a field F and x,EX. Show that M is a hyperspace iff xo+ M is a hyperplane and xo€ xo+M. bState Hahn-Banach theorem and write with prove an application about it. Show that every singleten subset and finite subset of a normed space is closed. Oxfallet f he a function from a normad roace YI Show tha ir continuour aty.GYiffarrow_forward7 3 2 x+11x+24 9 2 5 x+11x+24arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY