
Concept explainers
Two circular aluminum pipes of equal length L = 24 in. arc loaded by torsional moments T (sec figure). Pipe I has outside and inside diameters d2= 3 in. and L2, = 2.5 in., respectively. Pipe 2 has a constant outer diameter of d2along its entire length L and an inner diameter of d1but has an increased inner diameter of d3= 2.65 in. over the middle third.
Assume that E = 10,400 ksi, u = 0.33, and allowable shear stress ra= 6500 psi.
- Find the maximum acceptable torques that can be applied to Pipe 1; repeat for Pipe 2.
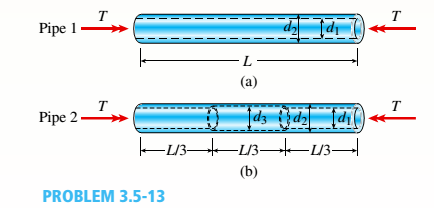
(a)
The maximum acceptable torques for pipe (1).
The maximum acceptable torques for pipe (2).
Answer to Problem 3.5.13P
Maximum acceptable torques for pipe (1) is =
Maximum acceptable torques for pipe (2) is =
Explanation of Solution
Given information:
The following figure shows the free body diagram of pipe 1:
Figure-(1) shows the diagram of two pipes:
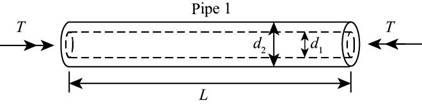
Figure-(1)
The following figure shows the free body diagram of pipe 2:
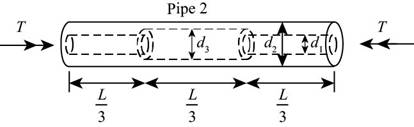
Figure-(2)
The length of pipe is
Write the expression for polar moment of inertia for pipe (1)
Here, the polar moment of inertia is
Write the expression for maximum torque for pipe (1)
Here, acceptable shear stress is
Write the expression for polar moment of inertia for pipe (2)
Here, the polar moment of inertia is
Write the expression for maximum torque for pipe (2)
Here, acceptable shear stress is
Calculation:
Substitute,
Substitute
Substitute,
Substitute
Conclusion:
Maximum acceptable torques for pipe (1) is =
Maximum acceptable torques for pipe (2) is =
(b)
The maximum acceptable length of the middle segment.
Answer to Problem 3.5.13P
The maximum acceptable length of the middle segment.
Explanation of Solution
Given information:
Maximum twist of pipe (2) cannot exceed
Write the expression for the angle of twist for pipe (1).
Here the angle of twist is
Write the expression for total angle of twist for pipe (2)
Here, the total angle of twist is
Write the expression for the length of the segment
Write expression for the angle of twist in the section
Write expression for the angle of twist in the section
Write expression for the angle of twist in the section
Substitute
Write the expression for relation between
Calculation:
Substitute
Substitute
Substitute
Conclusion:
The maximum acceptable length of the middle segment is =
(c)
The inner diameter for the given parameters.
Answer to Problem 3.5.13P
The inner diameter for the given parameters is =
Explanation of Solution
Given information:
the maximum torque carried by pipe (2) is
Write the expression for allowable torque.
Here, the allowable torque is
Substitute
Calculation:
Substitute
Conclusion:
The inner diameter for the given parameters is
(c)
Applied torque on pipe (1)
Maximum twist of pipe (1)
Answer to Problem 3.5.13P
Applied torque on pipe (1) is =
Applied torque on pipe (2) is =
Maximum twist of pipe (1) is =
Explanation of Solution
Write the expression for maximum shear strain.
Here, maximum shear strain is
Write the expression for maximum shear stress.
Here, the maximum shear stress is
Write the expression for shear modulus of elasticity.
Write the expression for maximum torque for pipe (1)
Write the expression for maximum angle of twist for pipe (1)
Maximum angle of twist in pipe (1) is
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
Applied torque on pipe (1) is =
Applied torque on pipe (2) is =
Maximum twist of pipe (1) is =
Want to see more full solutions like this?
Chapter 3 Solutions
Mechanics of Materials (MindTap Course List)
- A steel riser pipe hangs from a drill rig located offshore in deep water (see figure). Separate segments are joined using bolted flange plages (see figure part b and photo). Assume that there are six bolts at each pipe segment connection. Assume that the total length of the riser pipe is L = 5000 ft: outer and inner diameters are d2= l6in.and d1= 15 in.; flange plate thickness t1= 1.75 in.; and bolt and washer diameters are db= 1.125 in..and dW. = 1.875 in., respectively. (a) If the entire length of the riser pipe is suspended in air. find the average normal stress a in each bolt, the average bearing stress abbeneath each washer, and the average shear stress t through the flange plate at each bolt location for the topmost bolted connection. (b) If the same riser pipe hangs from a drill rig at sea. what are the normal, bearing, and shear stresses in the connection? Obtain the weight densities of steel and sea water from Table I-1. Appendix I. Neglect the effect of buoyant foam casings on the riser pipearrow_forwardA square steel tube of a length L = 20 ft and width b2= 10.0 in. is hoisted by a crane (see figure). The lube hangs from a pin of diameter d that is held by the cables at points A and B. The cross section is a hollow square with an inner dimension b1= 8.5 in. and outer dimension b2= 10,0 in. The allowable shear stress in the pin is 8,700 psi. and the allowable bearing stress between the pin and the tube is 13,000 psi. Determine the minimum diameter of the pin in order to support the weight of the tube. Note: Disregard the rounded corners of the tube when calculating its weight.arrow_forwardSolve the preceding problem for the following data: diameter LO m, thickness 48 mm, pressure 22 MPa, modulus 210 GPa. and Poisson's ratio 0.29arrow_forward
- Solve the preceding problem for a W 200 × 41,7 shape with h = 166 mm, h = 205 mm. rw = 7.24 mm, tE= ILS mm,andV = 38 kN.arrow_forwardRepeat Problem 11.3-9. Use two C 150 × 12.2 steel shapes and assume that E = 205 GPa and L = 6 m.arrow_forwardA vertical pole of solid, circular cross section is twisted by horizontal forces P = 5kN acting at the ends of a rigid horizontal arm AB (see figure part a). The distance from the outside of the pole to the line of action of each force is c = 125 mm (sec figure part b) and the pole height L = 350 mm. (a) If the allowable shear stress in the pole is 30 MPa, what is the minimum required diameter dminof the pole? (b) What is the torsional stiffness of the pole (kN · m/rad)? Assume that G = 28 GPa. (c) If two translation al springs, each with stiffness k =2550 kN/m, are added at 2c/5 from A and B (see figure part c), repeat part (a) to find dmin. Hint: Consider the pole and pair of springs as "springs in parallel."arrow_forward
- A plumber's valve wrench is used to replace valves in plumbing fixtures. A simplified model of the wrench (see figure part a) consists of pipe AB (length L. outer diameter D inner diameter dy), which is fixed at A and has holes of a diameter dhon either side of the pipe at B. A solid, cylindrical bar CBD (lengths, diameter^) is inserted into the holes at B and only one force F = 55 lb is applied in the -Z direction at C to loosen the fixture valve at A (see figure part c). Let G = 11,800 ksi, v = 0.30, L = 4 in., a = 4.5 in., d2= 1.25 in., dx= 1 in., and dh= 0.25 in. Find the state of plane stress on the top of the pipe near A (at coordinates A" = 0,Y = Q,Z = d->12), and show all stresses on a plane stress element (see figure part b). Compute the principal stresses and maximum shear stress, and show them on properly rotated stress elementsarrow_forwardA cantilever beam(Z, = 6 ft) with a rectangular cross section (/> = 3.5 in., h = 12 in.) supports an upward load P = 35 kips at its free end. (a) Find the state of stress ((7T, o^., and r in ksi) on a plane-stress element at L/2 that is i/ = 8 in. up from the bottom of the beam. Find the principal normal stresses and maximum shear stress. Show these stresses on sketches of properly oriented elements. (b) Repeat part (a) if an axial compressive centroidal load N = 40 kips is added at Barrow_forwardCompare the angle of twist 1 for a thin-walled circular tube (see figure) calculated from the approximate theory for thin-walled bars with the angle of twist 2 calculated from the exact theory of torsion for circular bars, Express the ratio 12terms of the non-dimensional ratio ß = r/t. Calculate the ratio of angles of twist for ß = 5, 10, and 20. What conclusion about the accuracy of the approximate theory do you draw from these results?arrow_forward
- Repeat Problem 3.3-1, but now use a circular tube with outer diameter d0= 2.5 in. and inner diameter di= 1.5 in.arrow_forwardA rigid Trame ABC is formed by welding two steel pipes at B (see figure). Each pipe has cross-sectional area A = 11.31 × 10 mm2, moment of inertia I = 46.37 × 106 mm4, and outside diameter d = 200 mm. Find the maximum tensile and compressive stresses e1and e2, respectively, in the frame due to the load P = 8.0 kN if L = H = 1.4 m.arrow_forwardTwo pipes {L, = 2.5 m and L, = 1.5 m) are joined al B by flange plales (thickness (, = 14 mm) with five bolts [dlt, = 13 mm] arranged in a circular pal tor n (see figure). Also, each pipe segment is atlaehed to a wall (at .1 and ( '. see figure! using a base plate Uh = 15 mm) and four bolts (dM, = 16 mm). All bolts are tightened until just snug. Assume £, = 110 GPa,E2 = 73 GPa,», = 0.33,andv, = 0.25. Neglect the self-weight of the pipes, and assume the pipes are in a stress-free stale initially. The cross-sectional areas of the pipes are At = 1500 mm: and A2 = (3/5)4. The ollter diameter of Pipe 1 is 60 mm. The outer diameter of Pipe 2 is equal to the inner diameter of Pipe 1. The bolt radius r = 64 mm for both base and flange plates. (a) If torque '/'is applied at .v = Lt. find an expression for reactive torques Iit and IL in terms of T. (b) Find the maximum load variable /'(i.e., Tmal) if allowable torsional stress in the two pipes is Tall0* = 65 MPa-id Draw torsional moment iTMD i and torsional displacement (TDD) diagrams. Label all key ordinales. What is '/>.ll('.' (d) Find mail, if allowable shear and bearing stresses in the base plate and flange bolts cannot be exceeded. Assume allowable stresses in shear an.: :vari:'.g I all bolls are r |Nill, = 45 MPa andtr MaK =90 MPa. (e) Remove torque Tat x — L,. Now assume the flange-plate bolt holes are misaligned by some angle ß (see figure). Find the expressions for reactive torques Rx and R2 if the pipes are twisted to align the flange-plate bolt holes, bolts are then inserted, and the pipes released. (f) What is the maximum permissible misalignment angle ß mix if allowable stresses in shear and bearing for all bolts [from part (d)] are not to be exceeded?arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
