
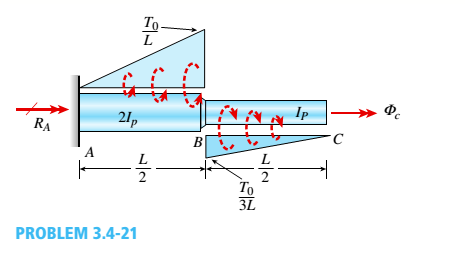
A nonprismatic bar ABC with a solid circular cross section is loaded by distributed torques (sec figure). The intensity of the torques, that is, the torque per unit distance, is denoted t(x) and varies linearly from zero at A to a maximum value T0/L at B. Segment BC has linearly distributed torque of intensity r(x) = T0/3L of opposite sign to that applied along AB. Also, the polar moment of inertia of AB is twice that of BC and the shear modulus of elasticity of the material is G.
- Find the reaction torque RA.
(a)
The reaction torque
Answer to Problem 3.4.21P
The reaction torque
Explanation of Solution
Given information:
The intensity of torque at point (A) is
Write the expression for equilibrium torque equation.
Here, the reaction torque is at point (A) is
Write the expression for the reaction torque is at point (A) from Equation (I)
Conclusion:
The reaction torque
(b)
The internal torsional moment in the segment
The internal torsional moment in the segment
Answer to Problem 3.4.21P
The internal torsional moment in the segment
The internal torsional moment in the segment
Explanation of Solution
Write the expression for internal torsional moment in section
Write the expression for internal torsional moment in section
Conclusion:
The internal torsional moment in the segment
The internal torsional moment in the segment
(c)
The twist rotation at point (C).
Answer to Problem 3.4.21P
The twist rotation at point (C) is
Explanation of Solution
Write the expression angle of twist at point (C).
Here, the angle of twist at point (C) is
Write the expression for polar moment of inertia of the bar.
Write the expression for polar moment of inertia in the section
Here, polar moment of inertia is in the section
Integrate Equation (IV).
Write the expression for angle of twist in
Here, angle of twist in section
Substitute
Substitute
Conclusion:
The twist rotation at point (C) is
(d)
The maximum stress and the location of maximum stress in the bar.
Answer to Problem 3.4.21P
The maximum stress is
The maximum stress in the bar is at point (A).
Explanation of Solution
Write the expression for the polar moment of inertia of section
Here, the polar moment of inertia is
Write the expression for the polar moment of inertia of section
Here, the polar moment of inertia is
Write the expression for the shear stress at point (A) from torsional equation.
Here, the shear stress is
Write the expression for the shear stress at point (A) from torsional equation.
Here, the shear stress is
Substitute
Substitute
Substitute,
Substitute
Conclusion:
The maximum stress is=
The maximum stress in the bar is at point (A).
(d)
The torsional moment diagrams.
Explanation of Solution
Write the torsional moment at point (A)
Write the torsional moment at point (B).
The following diagram shows the torsional moment diagram:

Figure-(1)
Want to see more full solutions like this?
Chapter 3 Solutions
Mechanics of Materials (MindTap Course List)
- A long, thin-walled tapered tube AB with a circular cross section (see figure) is subjected to a torque T. The tube has length L and constant wall thickness t. The diameter to the median lines of the cross sections at the ends A and B are dAand dB, respectively. Derive the following formula for the angle of twist of the tube: Hint: If the angle of taper is small, you may obtain approximate results by applying the formulas for a thin-walled prismatic tube to a differential element of the tapered tube and then integrating along the axis of the tube.arrow_forwardA solid circular bar A BCD with fixed supports at ends A and D is acted upon by two equal and oppositely directed torques T0, as shown in the figure. The torques arc applied at points B and C each of which is located at distance x from one end of the bar. (The distance x may vary from zero to L/2.) For what distance x will the angle of twist at points B and C be a maximum? What is the corresponding angle of twist 0max?arrow_forwardA tubular bar with outside diameterd2= 4.0 in, is twisted by torques T = 70,0 kip-in. (see figure). Under the action of these torques, the maximum tensile stress in the bar is found to be 6400 psi. Determine the inside diameter rtf of the bar. If the bar has length L = 48.0 in. and is made of aluminum with shear modulus G = 4,0 × 106 psi, what is the angle of twist d (in degrees) between the ends of the bar? (c) Determine the maximum shear strain y (in radians)?arrow_forward
- A stepped shaft ABC consisting of two solid, circular segments is subjected to uniformly distributed torque t1acting aver segment 1 and concentrated torque t2applied at C, as shown in the figure. Segment 1 of the shaft has a diameter of d1= 57 mm and length of L1= 0.75 m; segment 2 has a diameter d2— 44 mm and length L2= 0.5 m. Torque intensity /,"= 3100 N . m/m and T2= 1100 N. m. (a) Find reaction torque TAat support A. (b) Find the internal torque T(x) at two locations: .x = L1/2 and at .x = L1+ L2/2. Show these internal torques on properly drawn free-body diagrams.arrow_forwardA stepped shaft ABC consisting of two solid, circular segments is subjected to torques T}and T2acting in opposite directions, as shown in the figure. The larger segment of the shaft has a diameter of dv- 2.25 in. and a length Lt= 30 in.; the smaller segment has a diameter d2— 1.75 in. and a length L, = 20 in. The torques are T, = 21,000 lb-in. and fz=10.000 lb-in. (a) Find reaction torque TAat support A. (b) Find the internal torque T(x) at two locations: x = L1/2 and x = L1+ L2/2. Show these internal torques on properly drawn free-body diagrams (FBDs).arrow_forwardA vertical pole of solid, circular cross section is twisted by horizontal forces P = 5kN acting at the ends of a rigid horizontal arm AB (see figure part a). The distance from the outside of the pole to the line of action of each force is c = 125 mm (sec figure part b) and the pole height L = 350 mm. (a) If the allowable shear stress in the pole is 30 MPa, what is the minimum required diameter dminof the pole? (b) What is the torsional stiffness of the pole (kN · m/rad)? Assume that G = 28 GPa. (c) If two translation al springs, each with stiffness k =2550 kN/m, are added at 2c/5 from A and B (see figure part c), repeat part (a) to find dmin. Hint: Consider the pole and pair of springs as "springs in parallel."arrow_forward
- A uniformly tapered tube AB with a hollow circular cross section is shown in the figure. The tube has constant wall thickness t and length L, The average diameters at the ends are dAand dB= 2dA. The polar moment of inertia may be represented by the approximate formula Ipttd3t4[see Eq. (3-21)]. Derive a formula for the angle of twist e of the tube when it is subjected to torques T acting at the ends.arrow_forwardA prismatic bar AB of length L and solid circular cross section (diameter d) is loaded by a distributed torque of constant intensity t per unit distance (sec figure). Determine the maximum shear stress tmaxin the bar. Determine the angle of twist between t the ends of the bar.arrow_forwardA stepped shaft ACE is held against rotation at ends A and B and subjected to a torque T0acting at section C(see figure). The two segments of the shaft (AC and CB) have diameters dAand dg, respectively, and polar moments of inertia IpAand IpBrespectively. The shaft has length L and segment AC has length a. For what ratio a/L will the maximum shear stresses be the same in both segments of the shaft? For what ratio a/L will the internal torques be the same in both segments of the shaft?arrow_forward
- A stepped shaft consisting of solid circular segments having diameters D1= 2.0 in, and D2= 2.4 in. (see figure) is subjected to torques T. The radius of the fillet is R = 0,1 in. If the allowable shear stress at the stress concentration is 6000 psi, what is the maximum permissible torque Tmax?arrow_forwardA solid circular bar ABCD with fixed supports is acted upon by torques T0and 2T0at the locations shown in the figure. (a) Obtain a formula for the maximum angle of twist 0maxof the bar. (b) What is 0max if the applied torque T0at B is reversed in direction?arrow_forwardA prismatic bar AB with a solid circular cross section (diameter d) is loaded by a distributed torque (see figure). The intensity of the torque, that is, the torque per unit distance, is denoted i(x) and varies linearly from a maximum value iAat end A to zero at end B. Also, the length of the bar is L and the shear modulus of elasticity of the material is G. Determine the maximum shear stress in the bar. Determine the angle of twist between the ends of the bar.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
