
Concept explainers
(a)
The equation of motion of the scale.
Answer to Problem 3.39P
Explanation of Solution
Given:
Friction of the pivot and mass of the scale arm are neglected.
Concept used:
For an objects’ planar motion which rotates only about an axis perpendicular to the plane, the equation of motion can be written down using Newton’s Second Law.
Equation of Motion:
Where
Let the angular displacement be
The angular velocity,
Hence, the equation of motion of this object can be rewritten by substituting,
Derivation of Equation of motion:
Free body diagram:
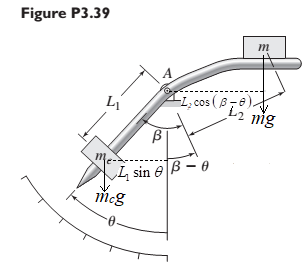
To find the equation of motion, the required unknowns are
The mass moment of Inertia, I about a specified reference axis is given as:
Where r = distance from the reference axis to mass element
Mass moment of Inertia of a rotating pendulum =
Inertia of mass,
Inertia of mass,
Total Inertia,
Sum of moments about the point, A:
Conclusion:
The equation of motion of the scale is
(b)
The equilibrium relation between weight and angle.
Answer to Problem 3.39P
Explanation of Solution
Given:
The system is in equilibrium.
Concept used:
For an objects’ planar motion which rotates only about an axis perpendicular to the plane, the equation of motion can be written down using Newton’s Second Law.
Equation of Motion:
Where
Let the angular displacement be
The angular velocity,
Hence, the equation of motion of this object can be rewritten by substituting,
Derivation of mg at equilibrium:
Free body diagram:
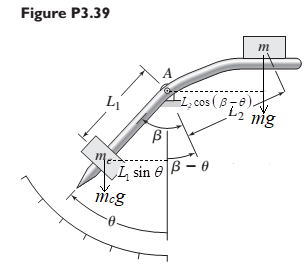
To find the equation of motion, the required unknowns are
The mass moment of Inertia, I about a specified reference axis is given as:
Where r = distance from the reference axis to mass element
Mass moment of Inertia of a rotating pendulum =
Inertia of mass,
Inertia of mass,
Total Inertia,
Sum of moments about the point, A:
At equilibrium, the angular acceleration,
Substitute the value of
Conclusion:
When system is at equilibrium, the relation between mg and
(c)
The value of weightof the object.
Answer to Problem 3.39P
22. 713N.
Explanation of Solution
Given:
The mass of counterweight,
Concept used:
For an objects’ planar motion which rotates only about an axis perpendicular to the plane, the equation of motion can be written down using Newton’s Second Law.
Equation of Motion:
Where
Let the angular displacement be
The angular velocity,
Hence, the equation of motion of this object can be rewritten by substituting,
Derivation of mg at equilibrium:
Free body diagram:
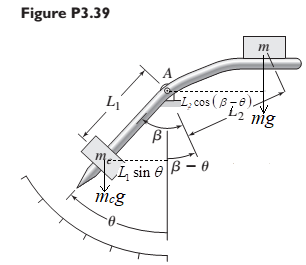
To find the equation of motion, the required unknowns are
The mass moment of Inertia, I about a specified reference axis is given as:
Where r = distance from the reference axis to mass element
Mass moment of Inertia of a rotating pendulum =
Inertia of mass,
Inertia of mass,
Total Inertia,
Sum of moments about the point, A:
At equilibrium, the angular acceleration,
Substitute the value of
Substitute the given values in equation
Conclusion:
The weight of the object is 22. 713N.
Want to see more full solutions like this?
Chapter 3 Solutions
System Dynamics
- ### Superheated steam powers a steam turbine for the production of electrical energy. The steam expands in the turbine and at an intermediate expansion pressure (0.1 Mpa) a fraction is extracted for a regeneration process in a surface regenerator. The turbine has an isentropic efficiency of 90% Design the simplified power plant schematic Analyze it on the basis of the attached figure Determine the power generated and the thermal efficiency of the plant ### Dados in the attached imagesarrow_forwardThe machine below forms metal plates through the application of force. Two toggles (ABC and DEF) transfer forces from the central hydraulic cylinder (H) to the plates that will be formed. The toggles then push bar G to the right, which then presses a plate (p) into the cavity, thus shaping it. In this case, the plate becomes a section of a sphere. If the hydraulic cylinder can produce a maximum force of F = 10 kN, then what is the maximum P value (i.e. Pmax) that can be applied to the plate when θ = 35°? Also, what are the compressive forces in the toggle rods in that situation? Finally, what happens to Pmax and the forces in the rods as θ decreases in magnitude?arrow_forwardDetermine the magnitude of the minimum force P needed to prevent the 20 kg uniform rod AB from sliding. The contact surface at A is smooth, whereas the coefficient of static friction between the rod and the floor is μs = 0.3.arrow_forward
- Determine the magnitudes of the reactions at the fixed support at A.arrow_forwardLet Hill frame H = {i-hat_r, i-hat_θ, i-hat_h} be the orbit frame of the LMO satellite. These base vectors are generally defined as:i-hat_r = r_LM / |r_LM|, i-hat_theta = i-hat_h X i-hat_r, i-hat_h = r_LM X r-dot_LMO /( | r_LM X r-dot_LMO | ) How would you: • Determine an analytic expressions for [HN]arrow_forwardDe Moivre’s Theoremarrow_forward
- hand-written solutions only, please.arrow_forwardDetermine the shear flow qqq for the given profile when the shear forces acting at the torsional center are Qy=30Q_y = 30Qy=30 kN and Qz=20Q_z = 20Qz=20 kN. Also, calculate qmaxq_{\max}qmax and τmax\tau_{\max}τmax. Given:Iy=10.5×106I_y = 10.5 \times 10^6Iy=10.5×106 mm4^44,Iz=20.8×106I_z = 20.8 \times 10^6Iz=20.8×106 mm4^44,Iyz=6×106I_{yz} = 6 \times 10^6Iyz=6×106 mm4^44. Additional parameters:αy=0.5714\alpha_y = 0.5714αy=0.5714,αz=0.2885\alpha_z = 0.2885αz=0.2885,γ=1.1974\gamma = 1.1974γ=1.1974. (Check hint: τmax\tau_{\max}τmax should be approximately 30 MPa.)arrow_forwardhand-written solutions only, please.arrow_forward
- In the bending of a U-profile beam, the load path passes through the torsional center C, causing a moment of 25 kNm at the cross-section under consideration. Additionally, the beam is subjected to an axial tensile force of 100 kN at the centroid. Determine the maximum absolute normal stress.(Check hint: approximately 350 MPa, but where?)arrow_forward### Make an introduction to a report of a rocket study project, in the OpenRocket software, where the project consists of the simulation of single-stage and two-stage rockets, estimating the values of the exhaust velocities of the engines used, as well as obtaining the graphs of "altitude", "mass ratio x t", "thrust x t" and "ψ × t".arrow_forwardA 6305 ball bearing is subjected to a steady 5000-N radial load and a 2000-N thrust load and uses a very clean lubricant throughout its life. If the inner race angular velocity is 500 rpm find The equivalent radial load the L10 life and the L50 lifearrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





