Chapter 3, Problem 10CRP

Agriculture: Bell Peppers The pathogen Phytophthora capsici causes bell pepper plants to wilt and die. A research project was designed to study the effect of soil water content and the spread of the disease in fields of bell peppers (Source: Journal of Agricultural, Biological, and Environmental Statistics, Vol. 2, No. 2). It is thought that too much water helps spread the disease. The fields were divided into rows and quadrants. The soil water content (percent of water by volume of soil) was determined for each plot. An important first step in such a research project is to give a statistical description of the data.

soil water content for bell Pepper study

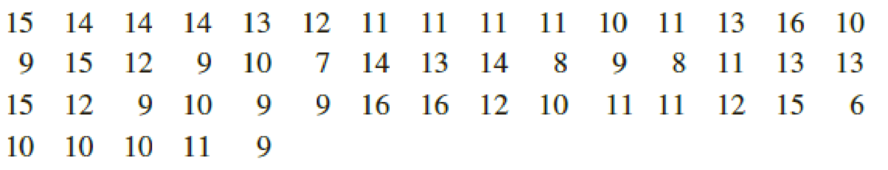
1. (a) Make a box-and-whisker plot of the data. Find the interquartile range.
2. (b) Grouped Data Make a frequency table using four classes. Then estimate the mean and sample standard deviation using the frequency table. Compute a 75% Chebyshev interval centered about the mean.
3. (c) If you have a statistical calculator or computer, use it to find the actual sample mean and sample standard deviation.

To determine

Draw the box-and-whisker plot.

Find the interquartile range.

Answer to Problem 10CRP

The box-and-whisker plot is shown below:

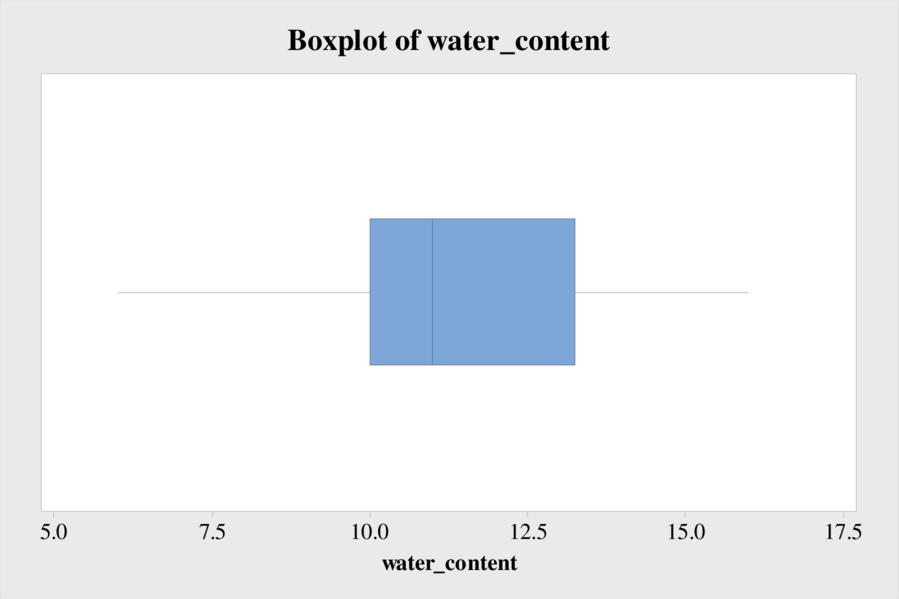
The interquartile range is 3.25.

Explanation of Solution

Step-by-step procedure to draw the box-and-whisker plot using MINITAB software:

• Choose Graph > Boxplot or Stat > EDA > Boxplot.
• Under One Y, choose Simple. Click OK.
• In Graph variables, enter the data of water_content.
• Click OK in all dialogue boxes.

Step-by-step procedure to obtain the interquartile range using MINITAB software:

• Choose Stat > Basic Statistics > Display Descriptive Statistics.
• In Variables enter the columns water_content.
• Check Options, Select Interquartile range.
• Click OK in all dialogue boxes.

Output obtained using the MINITAB software is given below:

From the output, the interquartile range is 3.25.

To determine

Create a table for a frequency table with four classes.

Find the mean and sample standard deviation using the frequency table.

Find the 75% Chebyshev interval centered about the mean.

Answer to Problem 10CRP

The frequency distribution table is given below:

Class Limits	Midpoints	Frequency
6-8	7	4
9-11	10	24
12-14	13	15
15-17	16	7

The value of the sample mean is 11.5.

Thesample standard deviation is 2.52.

The 75% Chebyshev interval centered about the mean isbetween 6.46 and 16.54.

Explanation of Solution

Midpoint:

The midpoint is calculated as given below:

$\text{Midpoint=}\frac{\left(\text{Lower class limit}+\text{Upper class limit}\right)}{2}$

Frequency:

Frequency is the number of data points that fall under each class.

From the given data set, the largest data point is 16 and the smallest data point is 6.

Class Width:

The class width is calculated as follows:

$\begin{array}{c}\text{Class width=}\frac{\left(\text{Largest data point}-\text{Smallest data point}\right)}{\text{Number of classes}}\\ \text{=}\frac{\left(16-6\right)}{4}\\ =2.5\\ \approx 3\end{array}$

The class width is 3. Hence, the lower class limit for the second class 9 is calculated by adding 3 to 6. Following this pattern, all the lower class limits are established. Then, the upper class limits are calculated.

The frequency distribution table is given below:

Class Limits	Midpoints	Frequency
6-8	7	4
9-11	10	24
12-14	13	15
15-17	16	7

The formulaefor the sample mean, the sample variance, and the sample standard deviation for grouped data aregiven below:

$\begin{array}{c}\overline{x}=\frac{{\displaystyle \sum xf}}{n}\\ s^2=\frac{{\displaystyle \sum {\left(x-\overline{x}\right)}^{2}f}}{n-1}\\ s=\sqrt{\frac{{\displaystyle \sum {\left(x-\overline{x}\right)}^{2}f}}{n-1}}\end{array}$

Where, x is the midpoint, $\overline{x}$ is the mean, n is the total number of values in the data, and f is the number of entries in that class.

The midpoint and the frequency areobtained from the histogram.

The value of ${\displaystyle \sum xf}$ is obtained below:

Midpoint (x)	Frequency (f)	xf
7	4	28
10	24	240
13	15	195
16	7	112
	${\displaystyle \sum f}=n=50$	${\displaystyle \sum xf}=575$

The value of sample mean is obtained below:

$\begin{array}{c}\overline{x}=\frac{575}{50}\\ =11.5\end{array}$

Thus, the value of the sample mean is 11.5.

The value of ${\displaystyle \sum {\left(x-\overline{x}\right)}^{2}f}$ is obtained below:

Midpoint (x)	Frequency (f)	$x-\overline{x}$	${\left(x-\overline{x}\right)}^2$	${\left(x-\overline{x}\right)}^{2}f$
7	4	–4.5	20.25	81
10	24	–1.5	2.25	54
13	15	1.5	2.25	33.75
16	7	4.5	20.25	141.75
				${\displaystyle \sum {\left(x-\overline{x}\right)}^{2}f}=310.5$

The sample standard deviation is obtained below:

$\begin{array}{c}s=\sqrt{\frac{310.5}{50-1}}\\ =\sqrt{\frac{310.5}{49}}\\ =2.52\end{array}$

Thus, the sample standard deviation is 2.52.

The 75% Chebyshev interval centered on the mean is obtained below:

$\begin{array}{c}\overline{x}-2s=11.5-2\left(2.52\right)\\ =11.5-5.04\\ =6.46\\ \overline{x}+2s=11.5+2\left(2.52\right)\\ =11.5+5.04\\ =16.54\end{array}$

Thus, the 75% Chebyshev interval centered about the mean isbetween 6.46 and 16.54.

To determine

Find the actual sample mean and sample standard deviation using a statistical computer.

Answer to Problem 10CRP

The value of actual sample mean is 11.5.

The value of sample standard deviation is 2.44.

Explanation of Solution

Step-by-step procedure to obtain the mean and standard deviation using MINITAB software:

• Choose Stat > Basic Statistics > Display Descriptive Statistics.
• In Variables enter the columns Percentage_Democrats.
• Check Options, Select Mean, and standard deviation.
• Click OK in all dialogue boxes.

Output obtained using the MINITAB software is given below:

From the MINITAB output, the value of actual sample mean is 11.5 and the value of sample standard deviation is 2.44.