Algebra 2
1st Edition
ISBN: 9780078884825
Author: McGraw-Hill/Glencoe
Publisher: Glencoe/McGraw-Hill School Pub Co
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 2.2, Problem 63STP
To determine
To state: the domain and range of relation. Then determine whether relation is a function, if it is determine if it is one-to-one, onto, both , or neither.
Expert Solution & Answer
Answer to Problem 63STP
Domain and Range are all real numbers.
The relation is a function.
The function is one-to-one and onto.
Explanation of Solution
Given information:
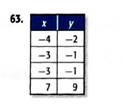
Formula used:
A function is a relation in which each element of the domain is paired with exactly one element in the range.
One-to −One function: Each element of the domain pairs exactly one unique element of the range.
Onto function: Each element of the range corresponds to an element of the domain.
Vertical−Test: If no vertical line intersects a graph in more than one point, the graph represents a function whereas if vertical line intersects a graph more than one point ,the graph does not represent a function.
Calculation:
According to the question ,
Every real number is the x -coordinate of points showed in table and every real number is
y -coordinate of points showed in table.
So, the domain and range are both all real numbers.
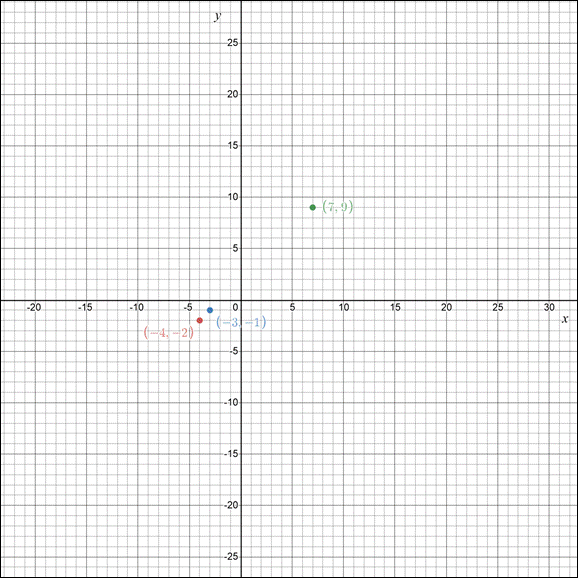
The graph passes the vertical test. Therefore, it is a function.
The graph shows the following coordinates:
Every x -value is paired with exactly one unique y -value, and every y -value corresponds to an x -value.
Thus, the function is both one-to-one and onto.
Chapter 2 Solutions
Algebra 2
Ch. 2.1 - Prob. 1ACYPCh. 2.1 - Prob. 1BCYPCh. 2.1 - Prob. 2CYPCh. 2.1 - Prob. 3CYPCh. 2.1 - Prob. 4ACYPCh. 2.1 - Prob. 4BCYPCh. 2.1 - Prob. 1CYUCh. 2.1 - Prob. 2CYUCh. 2.1 - Prob. 3CYUCh. 2.1 - Prob. 4CYU
Ch. 2.1 - Prob. 5CYUCh. 2.1 - Prob. 6CYUCh. 2.1 - Prob. 7CYUCh. 2.1 - Prob. 8CYUCh. 2.1 - Prob. 9CYUCh. 2.1 - Prob. 10CYUCh. 2.1 - Prob. 11PPSCh. 2.1 - Prob. 12PPSCh. 2.1 - Prob. 13PPSCh. 2.1 - Prob. 14PPSCh. 2.1 - Prob. 15PPSCh. 2.1 - Prob. 16PPSCh. 2.1 - Prob. 17PPSCh. 2.1 - Prob. 18PPSCh. 2.1 - Prob. 19PPSCh. 2.1 - Prob. 20PPSCh. 2.1 - Prob. 21PPSCh. 2.1 - Prob. 22PPSCh. 2.1 - Prob. 23PPSCh. 2.1 - Prob. 24PPSCh. 2.1 - Prob. 25PPSCh. 2.1 - Prob. 26PPSCh. 2.1 - Prob. 27PPSCh. 2.1 - Prob. 28PPSCh. 2.1 - Prob. 29PPSCh. 2.1 - Prob. 30PPSCh. 2.1 - Prob. 31PPSCh. 2.1 - Prob. 32PPSCh. 2.1 - Prob. 33PPSCh. 2.1 - Prob. 34PPSCh. 2.1 - Prob. 35HPCh. 2.1 - Prob. 36HPCh. 2.1 - Prob. 37HPCh. 2.1 - Prob. 38HPCh. 2.1 - Prob. 39HPCh. 2.1 - Prob. 40HPCh. 2.1 - Prob. 41HPCh. 2.1 - Prob. 42HPCh. 2.1 - Prob. 43HPCh. 2.1 - Prob. 44HPCh. 2.1 - Prob. 45STPCh. 2.1 - Prob. 46STPCh. 2.1 - Prob. 47STPCh. 2.1 - Prob. 48STPCh. 2.1 - Prob. 49STPCh. 2.1 - Prob. 50STPCh. 2.1 - Prob. 51STPCh. 2.1 - Prob. 52STPCh. 2.1 - Prob. 53STPCh. 2.1 - Prob. 54STPCh. 2.1 - Prob. 55STPCh. 2.1 - Prob. 56SCh. 2.1 - Prob. 57SCh. 2.1 - Prob. 58SCh. 2.1 - Prob. 59SCh. 2.1 - Prob. 60SCh. 2.1 - Prob. 61SCh. 2.1 - Prob. 62SCh. 2.1 - Prob. 63SCh. 2.1 - Prob. 64SCh. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.2 - Prob. 1ACYPCh. 2.2 - Prob. 1BCYPCh. 2.2 - Prob. 2ACYPCh. 2.2 - Prob. 2BCYPCh. 2.2 - Prob. 3ACYPCh. 2.2 - Prob. 3BCYPCh. 2.2 - Prob. 4CYPCh. 2.2 - Prob. 1CYUCh. 2.2 - Prob. 2CYUCh. 2.2 - Prob. 3CYUCh. 2.2 - Prob. 4CYUCh. 2.2 - Prob. 5CYUCh. 2.2 - Prob. 6CYUCh. 2.2 - Prob. 7CYUCh. 2.2 - Prob. 8CYUCh. 2.2 - Prob. 9CYUCh. 2.2 - Prob. 10CYUCh. 2.2 - Prob. 11CYUCh. 2.2 - Prob. 12CYUCh. 2.2 - Prob. 13CYUCh. 2.2 - Prob. 14CYUCh. 2.2 - Prob. 15CYUCh. 2.2 - Prob. 16PPSCh. 2.2 - Prob. 17PPSCh. 2.2 - Prob. 18PPSCh. 2.2 - Prob. 19PPSCh. 2.2 - Prob. 20PPSCh. 2.2 - Prob. 21PPSCh. 2.2 - Prob. 22PPSCh. 2.2 - Prob. 23PPSCh. 2.2 - Prob. 24PPSCh. 2.2 - Prob. 25PPSCh. 2.2 - Prob. 26PPSCh. 2.2 - Prob. 27PPSCh. 2.2 - Prob. 28PPSCh. 2.2 - Prob. 29PPSCh. 2.2 - Prob. 30PPSCh. 2.2 - Prob. 31PPSCh. 2.2 - Prob. 32PPSCh. 2.2 - Prob. 33PPSCh. 2.2 - Prob. 34PPSCh. 2.2 - Prob. 35PPSCh. 2.2 - Prob. 36PPSCh. 2.2 - Prob. 37PPSCh. 2.2 - Prob. 38PPSCh. 2.2 - Prob. 39PPSCh. 2.2 - Prob. 40PPSCh. 2.2 - Prob. 41PPSCh. 2.2 - Prob. 42PPSCh. 2.2 - Prob. 43PPSCh. 2.2 - Prob. 44PPSCh. 2.2 - Prob. 45PPSCh. 2.2 - Prob. 46PPSCh. 2.2 - Prob. 47PPSCh. 2.2 - Prob. 48PPSCh. 2.2 - Prob. 49PPSCh. 2.2 - Prob. 50PPSCh. 2.2 - Prob. 51PPSCh. 2.2 - Prob. 52HPCh. 2.2 - Prob. 53HPCh. 2.2 - Prob. 54HPCh. 2.2 - Prob. 55HPCh. 2.2 - Prob. 56HPCh. 2.2 - Prob. 57HPCh. 2.2 - Prob. 58HPCh. 2.2 - Prob. 59HPCh. 2.2 - Prob. 60HPCh. 2.2 - Prob. 61STPCh. 2.2 - Prob. 62STPCh. 2.2 - Prob. 63STPCh. 2.2 - Prob. 64STPCh. 2.2 - Prob. 65STPCh. 2.2 - Prob. 66STPCh. 2.2 - Prob. 67STPCh. 2.2 - Prob. 68STPCh. 2.2 - Prob. 69SCh. 2.2 - Prob. 70SCh. 2.2 - Prob. 71SCh. 2.2 - Prob. 72SCh. 2.2 - Prob. 73SCh. 2.2 - Prob. 74SCh. 2.2 - Prob. 75SCh. 2.2 - Prob. 76SCh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.3 - Prob. 1CYPCh. 2.3 - Prob. 2CYPCh. 2.3 - Prob. 3ACYPCh. 2.3 - Prob. 3BCYPCh. 2.3 - Prob. 4ACYPCh. 2.3 - Prob. 4BCYPCh. 2.3 - Prob. 1CYUCh. 2.3 - Prob. 2CYUCh. 2.3 - Prob. 3CYUCh. 2.3 - Prob. 4CYUCh. 2.3 - Prob. 5CYUCh. 2.3 - Prob. 6CYUCh. 2.3 - Prob. 7CYUCh. 2.3 - Prob. 8CYUCh. 2.3 - Prob. 9PPSCh. 2.3 - Prob. 10PPSCh. 2.3 - Prob. 11PPSCh. 2.3 - Prob. 12PPSCh. 2.3 - Prob. 13PPSCh. 2.3 - Prob. 14PPSCh. 2.3 - Prob. 15PPSCh. 2.3 - Prob. 16PPSCh. 2.3 - Prob. 17PPSCh. 2.3 - Prob. 18PPSCh. 2.3 - Prob. 19PPSCh. 2.3 - Prob. 20PPSCh. 2.3 - Prob. 21PPSCh. 2.3 - Prob. 22PPSCh. 2.3 - Prob. 23PPSCh. 2.3 - Prob. 24PPSCh. 2.3 - Prob. 25PPSCh. 2.3 - Prob. 26PPSCh. 2.3 - Prob. 27PPSCh. 2.3 - Prob. 28PPSCh. 2.3 - Prob. 29PPSCh. 2.3 - Prob. 30PPSCh. 2.3 - Prob. 31PPSCh. 2.3 - Prob. 32PPSCh. 2.3 - Prob. 33PPSCh. 2.3 - Prob. 34PPSCh. 2.3 - Prob. 35PPSCh. 2.3 - Prob. 36HPCh. 2.3 - Prob. 37HPCh. 2.3 - Prob. 38HPCh. 2.3 - Prob. 39HPCh. 2.3 - Prob. 40HPCh. 2.3 - Prob. 41HPCh. 2.3 - Prob. 42HPCh. 2.3 - Prob. 43HPCh. 2.3 - Prob. 44HPCh. 2.3 - Prob. 45STPCh. 2.3 - Prob. 46STPCh. 2.3 - Prob. 47STPCh. 2.3 - Prob. 48STPCh. 2.3 - Prob. 49STPCh. 2.3 - Prob. 50STPCh. 2.3 - Prob. 51STPCh. 2.3 - Prob. 52STPCh. 2.3 - Prob. 53STPCh. 2.3 - Prob. 54STPCh. 2.3 - Prob. 55SCh. 2.3 - Prob. 56SCh. 2.3 - Prob. 57SCh. 2.4 - Prob. 1ACYPCh. 2.4 - Prob. 1BCYPCh. 2.4 - Prob. 2ACYPCh. 2.4 - Prob. 2BCYPCh. 2.4 - Prob. 3CYPCh. 2.4 - Prob. 4CYPCh. 2.4 - Prob. 1CYUCh. 2.4 - Prob. 2CYUCh. 2.4 - Prob. 3CYUCh. 2.4 - Prob. 4CYUCh. 2.4 - Prob. 5CYUCh. 2.4 - Prob. 6CYUCh. 2.4 - Prob. 7CYUCh. 2.4 - Prob. 8PPSCh. 2.4 - Prob. 9PPSCh. 2.4 - Prob. 10PPSCh. 2.4 - Prob. 11PPSCh. 2.4 - Prob. 12PPSCh. 2.4 - Prob. 13PPSCh. 2.4 - Prob. 14PPSCh. 2.4 - Prob. 15PPSCh. 2.4 - Prob. 16PPSCh. 2.4 - Prob. 17PPSCh. 2.4 - Prob. 18PPSCh. 2.4 - Prob. 19PPSCh. 2.4 - Prob. 20PPSCh. 2.4 - Prob. 21PPSCh. 2.4 - Prob. 22PPSCh. 2.4 - Prob. 23PPSCh. 2.4 - Prob. 24PPSCh. 2.4 - Prob. 25PPSCh. 2.4 - Prob. 26PPSCh. 2.4 - Prob. 27PPSCh. 2.4 - Prob. 28PPSCh. 2.4 - Prob. 29PPSCh. 2.4 - Prob. 30PPSCh. 2.4 - Prob. 31PPSCh. 2.4 - Prob. 32PPSCh. 2.4 - Prob. 33PPSCh. 2.4 - Prob. 34PPSCh. 2.4 - Prob. 35PPSCh. 2.4 - Prob. 36PPSCh. 2.4 - Prob. 37HPCh. 2.4 - Prob. 38HPCh. 2.4 - Prob. 39HPCh. 2.4 - Prob. 40HPCh. 2.4 - Prob. 41HPCh. 2.4 - Prob. 42HPCh. 2.4 - Prob. 43HPCh. 2.4 - Prob. 44HPCh. 2.4 - Prob. 45HPCh. 2.4 - Prob. 46HPCh. 2.4 - Prob. 47STPCh. 2.4 - Prob. 48STPCh. 2.4 - Prob. 49STPCh. 2.4 - Prob. 50STPCh. 2.4 - Prob. 51STPCh. 2.4 - Prob. 52STPCh. 2.4 - Prob. 53STPCh. 2.4 - Prob. 54STPCh. 2.4 - Prob. 55STPCh. 2.4 - Prob. 56STPCh. 2.4 - Prob. 57STPCh. 2.4 - Prob. 58STPCh. 2.4 - Prob. 59STPCh. 2.4 - Prob. 60SCh. 2.4 - Prob. 61SCh. 2.4 - Prob. 62SCh. 2.4 - Prob. 63SCh. 2.4 - Prob. 64SCh. 2.4 - Prob. 65SCh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.5 - Prob. 1CYPCh. 2.5 - Prob. 2CYPCh. 2.5 - Prob. 1CYUCh. 2.5 - Prob. 2CYUCh. 2.5 - Prob. 3PPSCh. 2.5 - Prob. 4PPSCh. 2.5 - Prob. 5PPSCh. 2.5 - Prob. 6PPSCh. 2.5 - Prob. 7PPSCh. 2.5 - Prob. 8PPSCh. 2.5 - Prob. 9PPSCh. 2.5 - Prob. 10PPSCh. 2.5 - Prob. 11PPSCh. 2.5 - Prob. 12HPCh. 2.5 - Prob. 13HPCh. 2.5 - Prob. 14HPCh. 2.5 - Prob. 15HPCh. 2.5 - Prob. 16HPCh. 2.5 - Prob. 17HPCh. 2.5 - Prob. 18HPCh. 2.5 - Prob. 19HPCh. 2.5 - Prob. 20HPCh. 2.5 - Prob. 21STPCh. 2.5 - Prob. 22STPCh. 2.5 - Prob. 23STPCh. 2.5 - Prob. 24STPCh. 2.5 - Prob. 25STPCh. 2.5 - Prob. 26STPCh. 2.5 - Prob. 27STPCh. 2.5 - Prob. 28STPCh. 2.5 - Prob. 29STPCh. 2.5 - Prob. 30SCh. 2.5 - Prob. 31SCh. 2.5 - Prob. 32SCh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.6 - Prob. 1CYPCh. 2.6 - Prob. 2ACYPCh. 2.6 - Prob. 2BCYPCh. 2.6 - Prob. 3CYPCh. 2.6 - Prob. 4ACYPCh. 2.6 - Prob. 4BCYPCh. 2.6 - Prob. 1CYUCh. 2.6 - Prob. 2CYUCh. 2.6 - Prob. 3CYUCh. 2.6 - Prob. 4CYUCh. 2.6 - Prob. 5CYUCh. 2.6 - Prob. 6CYUCh. 2.6 - Prob. 7CYUCh. 2.6 - Prob. 8CYUCh. 2.6 - Prob. 9CYUCh. 2.6 - Prob. 10CYUCh. 2.6 - Prob. 11CYUCh. 2.6 - Prob. 12PPSCh. 2.6 - Prob. 13PPSCh. 2.6 - Prob. 14PPSCh. 2.6 - Prob. 15PPSCh. 2.6 - Prob. 16PPSCh. 2.6 - Prob. 17PPSCh. 2.6 - Prob. 18PPSCh. 2.6 - Prob. 19PPSCh. 2.6 - Prob. 20PPSCh. 2.6 - Prob. 21PPSCh. 2.6 - Prob. 22PPSCh. 2.6 - Prob. 23PPSCh. 2.6 - Prob. 24PPSCh. 2.6 - Prob. 25PPSCh. 2.6 - Prob. 26PPSCh. 2.6 - Prob. 27PPSCh. 2.6 - Prob. 28PPSCh. 2.6 - Prob. 29PPSCh. 2.6 - Prob. 30PPSCh. 2.6 - Prob. 31PPSCh. 2.6 - Prob. 32PPSCh. 2.6 - Prob. 33PPSCh. 2.6 - Prob. 34PPSCh. 2.6 - Prob. 35PPSCh. 2.6 - Prob. 36PPSCh. 2.6 - Prob. 37PPSCh. 2.6 - Prob. 38PPSCh. 2.6 - Prob. 39PPSCh. 2.6 - Prob. 40HPCh. 2.6 - Prob. 41HPCh. 2.6 - Prob. 42HPCh. 2.6 - Prob. 43HPCh. 2.6 - Prob. 44HPCh. 2.6 - Prob. 45HPCh. 2.6 - Prob. 46HPCh. 2.6 - Prob. 47HPCh. 2.6 - Prob. 48HPCh. 2.6 - Prob. 49STPCh. 2.6 - Prob. 50STPCh. 2.6 - Prob. 51STPCh. 2.6 - Prob. 52STPCh. 2.6 - Prob. 53STPCh. 2.6 - Prob. 54STPCh. 2.6 - Prob. 55STPCh. 2.6 - Prob. 56STPCh. 2.6 - Prob. 57SCh. 2.6 - Prob. 58SCh. 2.6 - Prob. 59SCh. 2.7 - Prob. 1ACYPCh. 2.7 - Prob. 1BCYPCh. 2.7 - Prob. 2ACYPCh. 2.7 - Prob. 2BCYPCh. 2.7 - Prob. 3ACYPCh. 2.7 - Prob. 3BCYPCh. 2.7 - Prob. 4ACYPCh. 2.7 - Prob. 4BCYPCh. 2.7 - Prob. 5CYPCh. 2.7 - Prob. 1CYUCh. 2.7 - Prob. 2CYUCh. 2.7 - Prob. 3CYUCh. 2.7 - Prob. 4CYUCh. 2.7 - Prob. 5CYUCh. 2.7 - Prob. 6CYUCh. 2.7 - Prob. 7CYUCh. 2.7 - Prob. 8CYUCh. 2.7 - Prob. 9CYUCh. 2.7 - Prob. 10PPSCh. 2.7 - Prob. 11PPSCh. 2.7 - Prob. 12PPSCh. 2.7 - Prob. 13PPSCh. 2.7 - Prob. 14PPSCh. 2.7 - Prob. 15PPSCh. 2.7 - Prob. 16PPSCh. 2.7 - Prob. 17PPSCh. 2.7 - Prob. 18PPSCh. 2.7 - Prob. 19PPSCh. 2.7 - Prob. 20PPSCh. 2.7 - Prob. 21PPSCh. 2.7 - Prob. 22PPSCh. 2.7 - Prob. 23PPSCh. 2.7 - Prob. 24PPSCh. 2.7 - Prob. 25PPSCh. 2.7 - Prob. 26PPSCh. 2.7 - Prob. 27PPSCh. 2.7 - Prob. 28PPSCh. 2.7 - Prob. 29PPSCh. 2.7 - Prob. 30PPSCh. 2.7 - Prob. 31PPSCh. 2.7 - Prob. 32PPSCh. 2.7 - Prob. 33PPSCh. 2.7 - Prob. 34PPSCh. 2.7 - Prob. 35PPSCh. 2.7 - Prob. 36PPSCh. 2.7 - Prob. 37PPSCh. 2.7 - Prob. 38PPSCh. 2.7 - Prob. 39PPSCh. 2.7 - Prob. 40PPSCh. 2.7 - Prob. 41PPSCh. 2.7 - Prob. 42PPSCh. 2.7 - Prob. 43HPCh. 2.7 - Prob. 44HPCh. 2.7 - Prob. 45HPCh. 2.7 - Prob. 46HPCh. 2.7 - Prob. 47HPCh. 2.7 - Prob. 48HPCh. 2.7 - Prob. 49HPCh. 2.7 - Prob. 50HPCh. 2.7 - Prob. 51HPCh. 2.7 - Prob. 52STPCh. 2.7 - Prob. 53STPCh. 2.7 - Prob. 54STPCh. 2.7 - Prob. 55STPCh. 2.7 - Prob. 56STPCh. 2.7 - Prob. 57STPCh. 2.7 - Prob. 58STPCh. 2.7 - Prob. 59STPCh. 2.7 - Prob. 60STPCh. 2.7 - Prob. 61STPCh. 2.7 - Prob. 62STPCh. 2.7 - Prob. 63SCh. 2.7 - Prob. 64SCh. 2.7 - Prob. 65SCh. 2.8 - Prob. 1ACYPCh. 2.8 - Prob. 1BCYPCh. 2.8 - Prob. 2CYPCh. 2.8 - Prob. 3ACYPCh. 2.8 - Prob. 3BCYPCh. 2.8 - Prob. 1CYUCh. 2.8 - Prob. 2CYUCh. 2.8 - Prob. 3CYUCh. 2.8 - Prob. 4CYUCh. 2.8 - Prob. 5CYUCh. 2.8 - Prob. 6CYUCh. 2.8 - Prob. 7CYUCh. 2.8 - Prob. 8PPSCh. 2.8 - Prob. 9PPSCh. 2.8 - Prob. 10PPSCh. 2.8 - Prob. 11PPSCh. 2.8 - Prob. 12PPSCh. 2.8 - Prob. 13PPSCh. 2.8 - Prob. 14PPSCh. 2.8 - Prob. 15PPSCh. 2.8 - Prob. 16PPSCh. 2.8 - Prob. 17PPSCh. 2.8 - Prob. 18PPSCh. 2.8 - Prob. 19PPSCh. 2.8 - Prob. 20PPSCh. 2.8 - Prob. 21PPSCh. 2.8 - Prob. 22PPSCh. 2.8 - Prob. 23PPSCh. 2.8 - Prob. 24PPSCh. 2.8 - Prob. 25PPSCh. 2.8 - Prob. 26PPSCh. 2.8 - Prob. 27PPSCh. 2.8 - Prob. 28PPSCh. 2.8 - Prob. 29PPSCh. 2.8 - Prob. 30PPSCh. 2.8 - Prob. 31PPSCh. 2.8 - Prob. 32PPSCh. 2.8 - Prob. 33HPCh. 2.8 - Prob. 34HPCh. 2.8 - Prob. 35HPCh. 2.8 - Prob. 36HPCh. 2.8 - Prob. 37HPCh. 2.8 - Prob. 38HPCh. 2.8 - Prob. 39HPCh. 2.8 - Prob. 40HPCh. 2.8 - Prob. 41HPCh. 2.8 - Prob. 42STPCh. 2.8 - Prob. 43STPCh. 2.8 - Prob. 44STPCh. 2.8 - Prob. 45STPCh. 2.8 - Prob. 46STPCh. 2.8 - Prob. 47STPCh. 2.8 - Prob. 48STPCh. 2.8 - Prob. 49STPCh. 2.8 - Prob. 50STPCh. 2.8 - Prob. 51STPCh. 2.8 - Prob. 52STPCh. 2.8 - Prob. 53STPCh. 2.8 - Prob. 54STPCh. 2.8 - Prob. 55SCh. 2.8 - Prob. 56SCh. 2.8 - Prob. 57SCh. 2 - Prob. 1QCCh. 2 - Prob. 2QCCh. 2 - Prob. 3QCCh. 2 - Prob. 4QCCh. 2 - Prob. 5QCCh. 2 - Prob. 6QCCh. 2 - Prob. 7QCCh. 2 - Prob. 8QCCh. 2 - Prob. 9QCCh. 2 - Prob. 10QCCh. 2 - Prob. 11QCCh. 2 - Prob. 12QCCh. 2 - Prob. 13QCCh. 2 - Prob. 14QCCh. 2 - Prob. 15QCCh. 2 - Prob. 16QCCh. 2 - Prob. 1MCQCh. 2 - Prob. 2MCQCh. 2 - Prob. 3MCQCh. 2 - Prob. 4MCQCh. 2 - Prob. 5MCQCh. 2 - Prob. 6MCQCh. 2 - Prob. 7MCQCh. 2 - Prob. 8MCQCh. 2 - Prob. 9MCQCh. 2 - Prob. 10MCQCh. 2 - Prob. 11MCQCh. 2 - Prob. 12MCQCh. 2 - Prob. 13MCQCh. 2 - Prob. 14MCQCh. 2 - Prob. 15MCQCh. 2 - Prob. 16MCQCh. 2 - Prob. 17MCQCh. 2 - Prob. 18MCQCh. 2 - Prob. 19MCQCh. 2 - Prob. 20MCQCh. 2 - Prob. 21MCQCh. 2 - Prob. 22MCQCh. 2 - Prob. 23MCQCh. 2 - Prob. 24MCQCh. 2 - Prob. 25MCQCh. 2 - Prob. 1SGRCh. 2 - Prob. 2SGRCh. 2 - Prob. 3SGRCh. 2 - Prob. 4SGRCh. 2 - Prob. 5SGRCh. 2 - Prob. 6SGRCh. 2 - Prob. 7SGRCh. 2 - Prob. 8SGRCh. 2 - Prob. 9SGRCh. 2 - Prob. 10SGRCh. 2 - Prob. 11SGRCh. 2 - Prob. 12SGRCh. 2 - Prob. 13SGRCh. 2 - Prob. 14SGRCh. 2 - Prob. 15SGRCh. 2 - Prob. 16SGRCh. 2 - Prob. 17SGRCh. 2 - Prob. 18SGRCh. 2 - Prob. 19SGRCh. 2 - Prob. 20SGRCh. 2 - Prob. 21SGRCh. 2 - Prob. 22SGRCh. 2 - Prob. 23SGRCh. 2 - Prob. 24SGRCh. 2 - Prob. 25SGRCh. 2 - Prob. 26SGRCh. 2 - Prob. 27SGRCh. 2 - Prob. 28SGRCh. 2 - Prob. 29SGRCh. 2 - Prob. 30SGRCh. 2 - Prob. 31SGRCh. 2 - Prob. 32SGRCh. 2 - Prob. 33SGRCh. 2 - Prob. 34SGRCh. 2 - Prob. 35SGRCh. 2 - Prob. 36SGRCh. 2 - Prob. 37SGRCh. 2 - Prob. 38SGRCh. 2 - Prob. 39SGRCh. 2 - Prob. 40SGRCh. 2 - Prob. 41SGRCh. 2 - Prob. 42SGRCh. 2 - Prob. 43SGRCh. 2 - Prob. 44SGRCh. 2 - Prob. 45SGRCh. 2 - Prob. 46SGRCh. 2 - Prob. 47SGRCh. 2 - Prob. 48SGRCh. 2 - Prob. 49SGRCh. 2 - Prob. 50SGRCh. 2 - Prob. 51SGRCh. 2 - Prob. 52SGRCh. 2 - Prob. 53SGRCh. 2 - Prob. 54SGRCh. 2 - Prob. 55SGRCh. 2 - Prob. 56SGRCh. 2 - Prob. 57SGRCh. 2 - Prob. 58SGRCh. 2 - Prob. 59SGRCh. 2 - Prob. 60SGRCh. 2 - Prob. 61SGRCh. 2 - Prob. 62SGRCh. 2 - Prob. 1PTCh. 2 - Prob. 2PTCh. 2 - Prob. 3PTCh. 2 - Prob. 4PTCh. 2 - Prob. 5PTCh. 2 - Prob. 6PTCh. 2 - Prob. 7PTCh. 2 - Prob. 8PTCh. 2 - Prob. 9PTCh. 2 - Prob. 10PTCh. 2 - Prob. 11PTCh. 2 - Prob. 12PTCh. 2 - Prob. 13PTCh. 2 - Prob. 14PTCh. 2 - Prob. 15PTCh. 2 - Prob. 16PTCh. 2 - Prob. 17PTCh. 2 - Prob. 18PTCh. 2 - Prob. 19PTCh. 2 - Prob. 20PTCh. 2 - Prob. 1ECh. 2 - Prob. 2ECh. 2 - Prob. 1STPCh. 2 - Prob. 2STPCh. 2 - Prob. 3STPCh. 2 - Prob. 4STPCh. 2 - Prob. 5STPCh. 2 - Prob. 6STPCh. 2 - Prob. 7STPCh. 2 - Prob. 8STPCh. 2 - Prob. 9STPCh. 2 - Prob. 10STPCh. 2 - Prob. 11STPCh. 2 - Prob. 12STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
Solve the inequality 3x27 .
Precalculus
Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...
Algebra and Trigonometry (6th Edition)
Earnings A sociologist says, “Typically, men in the United States still earn more than women.” What does this s...
Introductory Statistics
In Exercises 7–14, write out the first eight terms of each series to show how the series starts. Then find the ...
University Calculus: Early Transcendentals (4th Edition)
Explain the meaning of the term “statistically significant difference” in statistics terminology.
Intro Stats, Books a la Carte Edition (5th Edition)
In hypothesis testing, the common level of significance is =0.05. Some might argue for a level of significance ...
Basic Business Statistics, Student Value Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- 2. What is the total length of the shortest path that goes from (0,4) to a point on the x-axis, then to a point on the line y = 6, then to (18.4)?arrow_forwardموضوع الدرس Prove that Determine the following groups Homz(QZ) Hom = (Q13,Z) Homz(Q), Hom/z/nZ, Qt for neN- (2) Every factor group of adivisible group is divisble. • If R is a Skew ficald (aring with identity and each non Zero element is invertible then every R-module is free.arrow_forwardI have ai answers but incorrectarrow_forward
- Answersarrow_forward************* ********************************* Q.1) Classify the following statements as a true or false statements: a. If M is a module, then every proper submodule of M is contained in a maximal submodule of M. b. The sum of a finite family of small submodules of a module M is small in M. c. Zz is directly indecomposable. d. An epimorphism a: M→ N is called solit iff Ker(a) is a direct summand in M. e. The Z-module has two composition series. Z 6Z f. Zz does not have a composition series. g. Any finitely generated module is a free module. h. If O→A MW→ 0 is short exact sequence then f is epimorphism. i. If f is a homomorphism then f-1 is also a homomorphism. Maximal C≤A if and only if is simple. Sup Q.4) Give an example and explain your claim in each case: Monomorphism not split. b) A finite free module. c) Semisimple module. d) A small submodule A of a module N and a homomorphism op: MN, but (A) is not small in M.arrow_forwardI need diagram with solutionsarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
What is a Relation? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=hV1_wvsdJCE;License: Standard YouTube License, CC-BY
RELATIONS-DOMAIN, RANGE AND CO-DOMAIN (RELATIONS AND FUNCTIONS CBSE/ ISC MATHS); Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=u4IQh46VoU4;License: Standard YouTube License, CC-BY