Calculus Volume 1
17th Edition
ISBN: 9781938168024
Author: Strang, Gilbert
Publisher: OpenStax College
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.2, Problem 58E
In the following exercises, use the graph of function
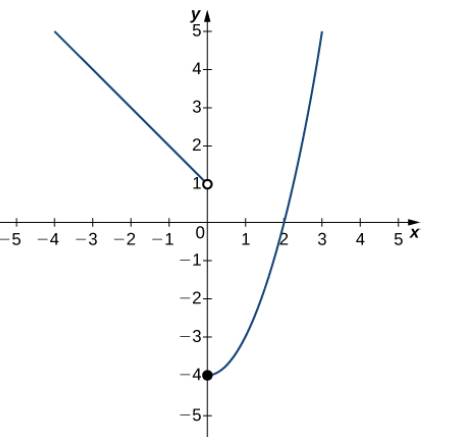
58.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
3) Which of the following are equivalent to 3? (There may be more than one that is
equivalent!)
-1
(a) (9)¯¹
3.
(b) (-3)-1
(c) (-3)
-1
(d) -(¯3)
(e) 11
3-1
(f) 3-4
Y- ___b=_____ (X- )
For each of the time series, construct a line chart of the data and identify the characteristics of the time series (that is, random, stationary, trend, seasonal, or cyclical)
Date IBM9/7/2010 $125.959/8/2010 $126.089/9/2010 $126.369/10/2010 $127.999/13/2010 $129.619/14/2010 $128.859/15/2010 $129.439/16/2010 $129.679/17/2010 $130.199/20/2010 $131.79
Chapter 2 Solutions
Calculus Volume 1
Ch. 2.1 - For the following exercises, points P(l, 2) and...Ch. 2.1 - For the following exercises, points P(l, 2) and...Ch. 2.1 - For the following exercises, points P(l, 2) and...Ch. 2.1 - For the following exercises, points P(l, 1) and...Ch. 2.1 - For the following exercises, points P(l, 1) and...Ch. 2.1 - For the following exercises, points P(l, 1) and...Ch. 2.1 - For the following exercises, points P(4, 2) and...Ch. 2.1 - For the following exercises, points P(4, 2) and...Ch. 2.1 - For the following exercises, points P(4, 2) and...Ch. 2.1 - For the following exercises, points P(l.5, 0) and...
Ch. 2.1 - For the following exercises, points P( 1.5, 0) and...Ch. 2.1 - For the following exercises, points P( 1.5, 0) and...Ch. 2.1 - For the following exercises, points P(-1, -1) and...Ch. 2.1 - For the following exercises, points P(-1,-1) and...Ch. 2.1 - For the following exercises, points P(-1, - 1) and...Ch. 2.1 - For the following exercises, the position function...Ch. 2.1 - For the following exercises, the position function...Ch. 2.1 - For the following exercises, consider a stone...Ch. 2.1 - For the following exercises, consider a stone...Ch. 2.1 - For the following exercises, consider a rocket...Ch. 2.1 - For the following exercises, consider a rocket...Ch. 2.1 - For the following exercises, consider an athlete...Ch. 2.1 - For the following exercises, consider an athlete...Ch. 2.1 - For the following exercises, consider the...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.1 - For the following exercises, consider the...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - Shock waves arise in many physical applications,...Ch. 2.2 - A track coach uses a camera with a fast shutter to...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - In the following exercises, use the limit Laws to...Ch. 2.3 - In the following exercises, use the limit laws to...Ch. 2.3 - In the following exercises, use the limit laws to...Ch. 2.3 - In the following exercises, use the limit laws to...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - ]In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - [T] In the following exercises, use a calculator...Ch. 2.3 - [T] In the following exercises, use a calculator...Ch. 2.3 - [T] In the following exercises, use a calculator...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - yIn the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - For the following problems, evaluate the limit...Ch. 2.3 - For the following problems, evaluate the limit...Ch. 2.3 - For the following problems, evaluate the limit...Ch. 2.3 - [T] In physics, the magnitude of an electric field...Ch. 2.3 - [T] The density of an object is given by its mass...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - Consider the graph of the function y=f(x) shown in...Ch. 2.4 - Let f(x)={3x,x1x3,x1 . Sketch the graph of f. Is...Ch. 2.4 - Let f(x)=x41x21forx1,1 . a. Sketch the graph of f....Ch. 2.4 - Sketch the graph of the function y=f(x) with...Ch. 2.4 - Sketch the graph of the function y=f(x) with...Ch. 2.4 - In the following exercises, suppose y=f(x) is...Ch. 2.4 - In the following exercises, suppose y=f(x) is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - [T] The following problems consider the scalar...Ch. 2.4 - [T] The following problems consider the scalar...Ch. 2.4 - [T] The following problems consider the scalar...Ch. 2.4 - [T] After a certain distance D has passed, the...Ch. 2.4 - As the rocket travels away from Earth’s surface,...Ch. 2.4 - wqProve the following functions are continuous...Ch. 2.4 - Prove the following functions are continuous...Ch. 2.4 - Prove the following functions are continuous...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - [T] In the following exercises, use a graphing...Ch. 2.5 - [T] In the following exercises, use a graphing...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - An engineer is using a machine to cut a flat...Ch. 2.5 - Use the precise definition of limit to prove that...Ch. 2.5 - Using precise definitions of limits, prove that...Ch. 2.5 - Using precise definitions of limits, prove that...Ch. 2.5 - Using precise definitions of limits, prove that...Ch. 2.5 - Using the function from the previous exercise, use...Ch. 2.5 - limxa(f(x)g(x))=LMCh. 2.5 - limxa[cf(x)]=cL for any real constant c (Hint....Ch. 2.5 - ...Ch. 2 - wTrue or False. In the following exercises,...Ch. 2 - True or False. In the following exercises, justify...Ch. 2 - True or False. In the following exercises, justify...Ch. 2 - True or False. In the following exercises, justify...Ch. 2 - Using the graph, find each limit or explain why...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - wIn the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, use the squeeze...Ch. 2 - In the following exercises, use the squeeze...Ch. 2 - In the following exercises, use the squeeze...Ch. 2 - In the following exercises, determine the value of...Ch. 2 - In the following exercises, determine the value of...Ch. 2 - In the following exercises, use the precise...Ch. 2 - In the following exercises, use the precise...Ch. 2 - A ball is thrown into the air and the vertical...Ch. 2 - A particle moving along a line has a displacement...Ch. 2 - From the previous exercises, estimate the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How many choices a...
A First Course in Probability (10th Edition)
In track, the second lane from the inside of the track is longer than the inside lane. Use this information to ...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Express the side length of a square as a function of the length d of the square’s diagonal. Then express the ar...
University Calculus: Early Transcendentals (4th Edition)
Arc length calculations Find the arc length of the following curves on the given interval by integrating with r...
Calculus: Early Transcendentals (2nd Edition)
CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...
Thinking Mathematically (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 5) State any theorems that you use in determining your solution. a) Suppose you are given a model with two explanatory variables such that: Yi = a +ẞ1x1 + ẞ2x2i + Ui, i = 1, 2, ... n Using partial differentiation derive expressions for the intercept and slope coefficients for the model above. [25 marks] b) A production function is specified as: Yi = α + B₁x1i + ẞ2x2i + Ui, i = 1, 2, ... n, u₁~N(0,σ²) where: y = log(output), x₁ = log(labor input), x2 = log(capital input) The results are as follows: x₁ = 10, x2 = 5, ỹ = 12, S11 = 12, S12= 8, S22 = 12, S₁y = 10, = 8, Syy = 10, S2y n = 23 (individual firms) i) Compute values for the intercept, the slope coefficients and σ². [20 marks] ii) Show that SE (B₁) = 0.102. [15 marks] iii) Test the hypotheses: ẞ1 = 1 and B2 = 0, separately at the 5% significance level. You may take without calculation that SE (a) = 0.78 and SE (B2) = 0.102 [20 marks] iv) Find a 95% confidence interval for the estimate ẞ2. [20 marks]arrow_forwardPage < 2 of 2 - ZOOM + The set of all 3 x 3 upper triangular matrices 6) Determine whether each of the following sets, together with the standard operations, is a vector space. If it is, then simply write 'Vector space'. You do not have to prove all ten vector space axioms. If it is not, then identify one of the ten vector space axioms with its number in the attached sheet that fails and also show that how it fails. a) The set of all polynomials of degree four or less. b) The set of all 2 x 2 singular matrices. c) The set {(x, y) : x ≥ 0, y is a real number}. d) C[0,1], the set of all continuous functions defined on the interval [0,1]. 7) Given u = (-2,1,1) and v = (4,2,0) are two vectors in R³-space. Find u xv and show that it is orthogonal to both u and v. 8) a) Find the equation of the least squares regression line for the data points below. (-2,0), (0,2), (2,2) b) Graph the points and the line that you found from a) on the same Cartesian coordinate plane.arrow_forward1. A consumer group claims that the mean annual consumption of cheddar cheese by a person in the United States is at most 10.3 pounds. A random sample of 100 people in the United States has a mean annual cheddar cheese consumption of 9.9 pounds. Assume the population standard deviation is 2.1 pounds. At a = 0.05, can you reject the claim? (Adapted from U.S. Department of Agriculture) State the hypotheses: Calculate the test statistic: Calculate the P-value: Conclusion (reject or fail to reject Ho): 2. The CEO of a manufacturing facility claims that the mean workday of the company's assembly line employees is less than 8.5 hours. A random sample of 25 of the company's assembly line employees has a mean workday of 8.2 hours. Assume the population standard deviation is 0.5 hour and the population is normally distributed. At a = 0.01, test the CEO's claim. State the hypotheses: Calculate the test statistic: Calculate the P-value: Conclusion (reject or fail to reject Ho): Statisticsarrow_forward
- Page < 1 of 2 - ZOOM + 1) a) Find a matrix P such that PT AP orthogonally diagonalizes the following matrix A. = [{² 1] A = b) Verify that PT AP gives the correct diagonal form. 2 01 -2 3 2) Given the following matrices A = -1 0 1] an and B = 0 1 -3 2 find the following matrices: a) (AB) b) (BA)T 3) Find the inverse of the following matrix A using Gauss-Jordan elimination or adjoint of the matrix and check the correctness of your answer (Hint: AA¯¹ = I). [1 1 1 A = 3 5 4 L3 6 5 4) Solve the following system of linear equations using any one of Cramer's Rule, Gaussian Elimination, Gauss-Jordan Elimination or Inverse Matrix methods and check the correctness of your answer. 4x-y-z=1 2x + 2y + 3z = 10 5x-2y-2z = -1 5) a) Describe the zero vector and the additive inverse of a vector in the vector space, M3,3. b) Determine if the following set S is a subspace of M3,3 with the standard operations. Show all appropriate supporting work.arrow_forwardFind the Laplace Transform of the function to express it in frequency domain form.arrow_forwardPlease draw a graph that represents the system of equations f(x) = x2 + 2x + 2 and g(x) = –x2 + 2x + 4?arrow_forward
- Given the following system of equations and its graph below, what can be determined about the slopes and y-intercepts of the system of equations? 7 y 6 5 4 3 2 -6-5-4-3-2-1 1+ -2 1 2 3 4 5 6 x + 2y = 8 2x + 4y = 12 The slopes are different, and the y-intercepts are different. The slopes are different, and the y-intercepts are the same. The slopes are the same, and the y-intercepts are different. O The slopes are the same, and the y-intercepts are the same.arrow_forwardChoose the function to match the graph. -2- 0 -7 -8 -9 --10- |--11- -12- f(x) = log x + 5 f(x) = log x - 5 f(x) = log (x+5) f(x) = log (x-5) 9 10 11 12 13 14arrow_forwardQ2 H let x(+) = &cos (Ait+U) and. 4(+) = ß cos(12t +V), where d. B. 1. In Constants and U,V indep.rus have uniform dist. (-π,π) Show that: ①Rxy (+,4+1)=0 @ Rxy (++) = cos [ when U=V Q3 let x(t) is stochastic process with Wss -121 e, and Rx ltst+1) = ( 2, show that E(X) = E(XS-X₁)² = 2(-1). Qu let x(t) = U Cost + (V+1) Sint, tεIR. where UV indep.rus, and let E (U)-E(V)=0 and E(U) = E(V) = 1, show that Cov (Xt, Xs) = K (t,s) = cos(s-t) X(+) is not WSS.arrow_forward
- Which of the following represents the graph of f(x)=3x-2? 7 6 5 4 ++ + + -7-6-5-4-3-2-1 1 2 3 4 5 6 7 -2 3 -5 6 -7 96 7 5 4 O++ -7-6-5-4-3-2-1 -2 -3 -4 -5 -7 765 432 -7-6-5-4-3-2-1 -2 ++ -3 -4 -5 -6 2 3 4 5 6 7 7 6 2 345 67 -7-6-5-4-3-2-1 2 3 4 5 67 4 -5arrow_forward21. find the mean. and variance of the following: Ⓒ x(t) = Ut +V, and V indepriv. s.t U.VN NL0, 63). X(t) = t² + Ut +V, U and V incepires have N (0,8) Ut ①xt = e UNN (0162) ~ X+ = UCOSTE, UNNL0, 62) SU, Oct ⑤Xt= 7 where U. Vindp.rus +> ½ have NL, 62). ⑥Xn = ΣY, 41, 42, 43, ... Yn vandom sample K=1 Text with mean zen and variance 6arrow_forwardA psychology researcher conducted a Chi-Square Test of Independence to examine whether there is a relationship between college students’ year in school (Freshman, Sophomore, Junior, Senior) and their preferred coping strategy for academic stress (Problem-Focused, Emotion-Focused, Avoidance). The test yielded the following result: image.png Interpret the results of this analysis. In your response, clearly explain: Whether the result is statistically significant and why. What this means about the relationship between year in school and coping strategy. What the researcher should conclude based on these findings.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY