
Concept explainers
Interpretation:
The reason as to why the
Concept introduction:
A unit cell of the crystal is the three-dimensional arrangement of the atoms present in the crystal. The unit cell is the smallest and simplest unit of the crystal which on repetition forms an entire crystal. Unit cell can be a cubic unit cell or hexagonal unit cell. The classification of a unit cell depends on the lattice site occupied by the atoms.
Answer to Problem 21.39E
The
Explanation of Solution
Consider a cube having a side of
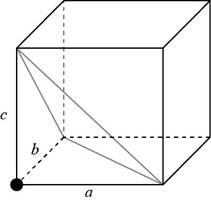
Figure 1
Similarly, consider another
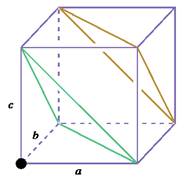
Figure 2
Both the planes are redrawn by using the atoms as shown below.
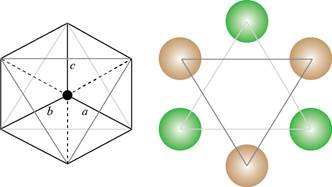
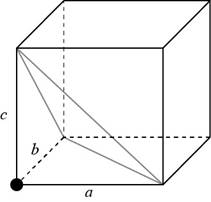
Figure 3
The repeating pattern of Figure 3 is drawn and the path of the diffracted light is shown below.
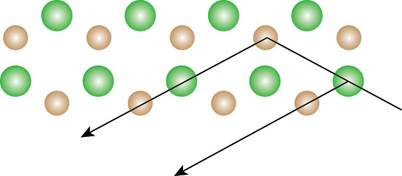
Figure 4
In the body-centered cubic lattice, the atoms are present at the center as well as at the corners. The light is diffracted by the center atoms. The path of diffracted light is shown below.
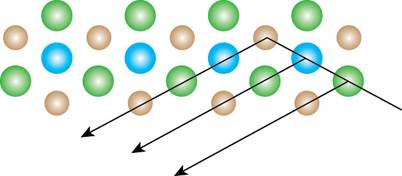
Figure 5
The above diagram is drawn according to the Bragg’s law. The representation of above diagram is shown below.
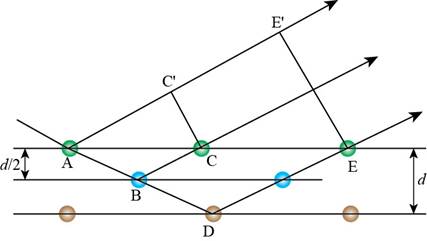
Figure 6
From the Figure 6, the extra distance covered by the light when it is diffracted by the yellow atom (D) is calculated as follows.
Where,
•
• .
•
The distance between two layers is
Substitute
Similarly, the extra distance covered by the light when it is diffracted by the blue atom (B) is calculated as follows.
Where,
•
•
The distance between two layers is
Substitute
Trigonometry is used to calculate the length of
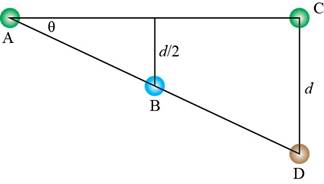
Figure 7
The expression for
The expression for
Substitute equation (5) in above expression.
The trigonometry is used to calculate the length of
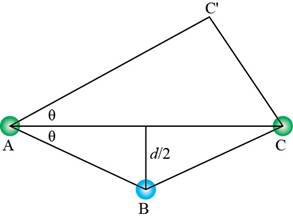
Figure 8
The expression for
The expression for
Substitute equation (8) in equation (7).
Similarly, trigonometry is used to calculate the length of
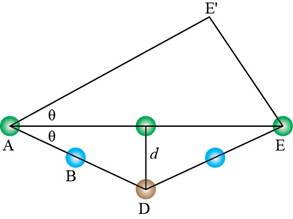
Figure 9
The expression for
The expression for
Substitute equation (11) in equation (10).
Substitute equation (8) in above expression.
Substitute equation (12) and equation (6) in equation (4).
Substitute equation (2) in the above expression.
The above expression shows that the length of thelight passed through the improperly diffracted path is half of the length of the light passed through the properly diffracted path. This indicates that only destructive interference is experienced by the light and it would be cancelled out. Therefore, the
The
Want to see more full solutions like this?
Chapter 21 Solutions
PHYSICAL CHEMISTRY-STUDENT SOLN.MAN.
- Determine the structures of the missing organic molecules in the following reaction: + H₂O +H OH O OH +H OH X Note: Molecules that share the same letter have the exact same structure. In the drawing area below, draw the skeletal ("line") structure of the missing organic molecule X. Click and drag to start drawing a structure.arrow_forwardIdentify the missing organic reactant in the following reaction: x + x O OH H* + ☑- X H+ O O Х Note: This chemical equation only focuses on the important organic molecules in the reaction. Additional inorganic or small-molecule reactants or products (like H₂O) are not shown. In the drawing area below, draw the skeletal ("line") structure of the missing organic reactant X. Click and drag to start drawing a structure. Carrow_forwardCH3O OH OH O hemiacetal O acetal O neither O 0 O hemiacetal acetal neither OH hemiacetal O acetal O neither CH2 O-CH2-CH3 CH3-C-OH O hemiacetal O acetal CH3-CH2-CH2-0-c-O-CH2-CH2-CH3 O neither HO-CH2 ? 000 Ar Barrow_forward
- What would be the best choices for the missing reagents 1 and 3 in this synthesis? 1. PPh3 2 2. n-BuLi 3 Draw the missing reagents in the drawing area below. You can draw them in any arrangement you like. • Do not draw the missing reagent 2. If you draw 1 correctly, we'll know what it is. • Note: if one of your reagents needs to contain a halogen, use bromine. Explanation Check Click and drag to start drawing a structure.arrow_forwardPredict the products of this organic reaction: NaBH3CN + NH2 ? H+ Click and drag to start drawing a structure. ×arrow_forwardPredict the organic products that form in the reaction below: + OH +H H+ ➤ ☑ X - Y Note: You may assume you have an excess of either reactant if the reaction requires more than one of those molecules to form the products. In the drawing area below, draw the skeletal ("line") structures of the missing organic products X and Y. You may draw the structures in any arrangement that you like, so long as they aren't touching. Click and drag to start drawing a structure. Garrow_forward
- Predict the organic products that form in the reaction below: OH H+ H+ + ☑ Y Note: You may assume you have an excess of either reactant if the reaction requires more than one of those molecules to form the products. In the drawing area below, draw the skeletal ("line") structures of the missing organic products X and Y. You may draw the structures in any arrangement that you like, so long as they aren't touching. Click and drag to start drawing a structure. ✓ marrow_forwardDetermine the structures of the missing organic molecules in the following reaction: + H₂O +H H+ Y Z ☑ ☑ Note: Molecules that share the same letter have the exact same structure. In the drawing area below, draw the skeletal ("line") structures of the missing organic molecules X, Y, and Z. You may draw the structures in any arrangement that you like, so long as they aren't touching. Molecule X shows up in multiple steps, but you only have to draw its structure once. Click and drag to start drawing a structure. AP +arrow_forwardPlease help, this is all the calculations i got!!! I will rate!!!Approx mass of KMnO in vial: 3.464 4 Moss of beaker 3×~0. z Nax200: = 29.9219 Massof weacerv after remosimgain N2C2O4. Need to fill in all the missing blanks. ง ง Approx mass of KMnO4 in vials 3.464 Mass of beaker + 3x ~0-304: 29.9219 2~0.20 Miss of beaker + 2x- 29.7239 Mass of beaker + 1x~0.2g Naz (204 29-5249 Mass of beaver after removing as qa Na₂ C₂O T1 T2 T3 Final Buiet reading Initial butet reading (int)) Hass of NaOr used for Titration -reading (mL) calculation Results: 8.5ml 17mL 27.4mL Oml Om Oml T1 T2 T3 Moles of No CO Moles of KMO used LOF KM. O used Molenty of KMNO Averagem Of KMOWLarrow_forward
- Draw the skeletal ("line") structure of 2-hydroxy-4-methylpentanal. Click and drag to start drawing a structure. Xarrow_forwardDetermine whether the following molecule is a hemiacetal, acetal, or neither and select the appropriate box below. Also, highlight the hemiacetal or acetal carbon if there is one. hemiacetal acetal Oneither OHarrow_forwardWhat is the missing reactant R in this organic reaction? ་ ་ ་ ་ ་ ་ ་ ་ ་ ་ +R H3O+ • Draw the structure of R in the drawing area below. N • Be sure to use wedge and dash bonds if it's necessary to draw one particular enantiomer. Click and drag to start drawing a structure.arrow_forward
 Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning, Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning





