Chapter 2.1, Problem 16P

A 250-mm-long aluminum tube (E = 70 GPa) of 36-mm outer diameter and 28-mm inner diameter can be closed at both ends by means of single-threaded screw-on covers of 1.5-mm pitch. With one cover screwed on tight, a solid brass rod (E = 105 GPa) of 25-mm diameter is placed inside the tube and the second cover is screwed on. Since the rod is slightly longer than the tube, it is observed that the cover must be forced against the rod by rotating it one-quarter of a turn before it can be tightly closed. Determine (a) the average normal stress in the tube and in the rod, (b) the deformations of the tube and of the rod.

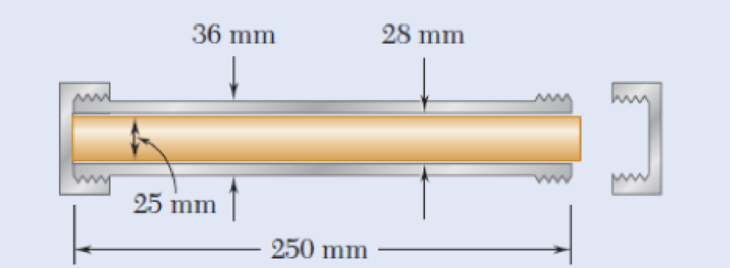
Fig. P2.16

To determine

The average normal stress in the tube $\left({\sigma }_{\text{t}}\right)$ and in the rod $\left({\sigma }_{\text{r}}\right)$.

Answer to Problem 16P

The average normal stress in the tube $\left({\sigma }_{\text{t}}\right)$ and in the rod $\left({\sigma }_{\text{r}}\right)$ are $\underset{\_}{67.9\text{MPa}}$ and $\underset{\_}{-55.6\text{MPa}}$.

Explanation of Solution

Given information:

The length of the tube (L) is $250\text{mm}$.

The outer diameter of the tube $\left(D_{\text{t}}\right)$ is $36\text{mm}$.

The inner diameter of the tube $\left(d_{\text{t}}\right)$ is $28\text{mm}$.

The Young’s modulus of the aluminium $\left(E_{\text{t}}\right)$ is $70\text{GPa}$.

The diameter of the rod $\left(d_{\text{r}}\right)$ is $25\text{mm}$.

The Young’s modulus of the brass $\left(E_{\text{r}}\right)$ is $105\text{GPa}$.

The pitch of the single-threaded screw-on cover (p) is $1.5\text{mm}$.

The load act in the tube is P.

Calculation:

Calculate the cross sectional area of the tube $\left(A_{\text{t}}\right)$ using the formula:

$A_{\text{t}}=\frac{\pi }{4}\left(D_{\text{t}}^2-d_{\text{t}}^2\right)$

Substitute $36\text{mm}$ for $D_{\text{t}}$ and $28\text{mm}$ for $d_{\text{t}}$.

$\begin{array}{c}{A}_{\text{t}}=\frac{\pi }{4}\times \left({36}^2-{28}^2\right)\\ =402.124{\text{mm}}^2\end{array}$

Calculate the cross sectional area of the rod $\left(A_{\text{r}}\right)$ using the formula:

$A_{\text{r}}=\frac{\pi }{4}{d}_{\text{r}}^2$

Substitute $25\text{mm}$ for $d_{\text{r}}$.

$\begin{array}{c}{A}_{\text{r}}=\frac{\pi }{4}\times {25}^2\\ =490.874{\text{mm}}^2\end{array}$

Calculate the deformation of the tube $\left({\delta }_{\text{t}}\right)$ using the formula:

${\delta }_{\text{t}}=\frac{PL}{A_{\text{t}}{E}_{\text{t}}}$

Substitute $250\text{mm}$ for L, $402.124{\text{mm}}^2$ for $A_{\text{t}}$, and $70\text{GPa}$ for $E_{\text{t}}$.

$\begin{array}{c}{\delta }_{\text{t}}=\frac{P\times 250}{402.124{\text{mm}}^2\times 70\text{GPa}\times \frac{{10}^3{\text{N/mm}}^2}{1\text{GPa}}}\\ =8.8814\times {10}^{-6}P\end{array}$

Calculate the deformation of the rod $\left({\delta }_{\text{r}}\right)$ using the formula:

${\delta }_{\text{r}}=-\frac{PL}{A_{\text{r}}{E}_{\text{r}}}$

Substitute $250\text{mm}$ for L, $490.874{\text{mm}}^2$ for $A_{\text{r}}$, and $105\text{GPa}$ for $E_{\text{r}}$.

$\begin{array}{c}{\delta }_{\text{r}}=-\frac{P\times 250}{490.874{\text{mm}}^2\times 105\text{GPa}\times \frac{{10}^3{\text{N/mm}}^2}{1\text{GPa}}}\\ =-4.8504\times {10}^{-6}P\end{array}$

Calculate the deformation of the screw $\left(\delta \right)$ using the formula:

$\delta =\frac{1}{4}p$

Substitute $1.5\text{mm}$ for p.

$\begin{array}{c}\delta =\frac{1}{4}\times 1.5\\ =0.375\text{mm}\end{array}$

Calculate the load (P) act in the tube using the formula:

$\delta ={\delta }_{\text{t}}-{\delta }_{\text{r}}$

Substitute $0.375\text{mm}$ for $\delta$, $-4.8504\times {10}^{-6}P$ for ${\delta }_{\text{r}}$, and $8.8814\times {10}^{-6}P$ for ${\delta }_{\text{t}}$.

$\begin{array}{c}0.375=-4.8504\times {10}^{-6}P-8.8814\times {10}^{-6}P\\ 0.375=1.37318\times {10}^{-5}P\\ P=\frac{0.375}{1.37318\times {10}^{-5}}\\ =27.308\times {10}^3\text{N}\end{array}$

Calculate the average normal stress in the tube $\left({\sigma }_{\text{t}}\right)$ using the formula:

${\sigma }_{\text{t}}=\frac{P}{A_{\text{t}}}$

Substitute $402.124{\text{mm}}^2$ for $A_{\text{t}}$ and $27.308\times {10}^3\text{N}$ for P.

$\begin{array}{c}{\sigma }_{\text{t}}=\frac{27.308\times {10}^3}{402.124}\\ =67.9{\text{N/mm}}^{\text{2}}\times \frac{1\text{MPa}}{1{\text{N/mm}}^2}\\ =67.9\text{MPa}\end{array}$

Calculate the average normal stress in the rod $\left({\sigma }_{\text{r}}\right)$ using the formula:

${\sigma }_{\text{r}}=-\frac{P}{A_{\text{r}}}$

Substitute $490.874{\text{mm}}^2$ for $A_{\text{r}}$ and $27.308\times {10}^3\text{N}$ for P.

$\begin{array}{c}{\sigma }_{\text{r}}=-\frac{27.308\times {10}^3}{490.874}\\ =-55.6{\text{N/mm}}^{\text{2}}\times \frac{1\text{MPa}}{1{\text{N/mm}}^2}\\ =-55.6\text{MPa}\end{array}$

Hence, the average normal stress in the tube $\left({\sigma }_{\text{t}}\right)$ and in the rod $\left({\sigma }_{\text{r}}\right)$ are $\underset{\_}{67.9\text{MPa}}$ and $\underset{\_}{-55.6\text{MPa}}$.

To determine

The deformations of the tube $\left({\delta }_{\text{t}}\right)$ and of the rod $\left({\delta }_{\text{r}}\right)$.

Answer to Problem 16P

The deformations of the tube $\left({\delta }_{\text{t}}\right)$ and of the rod $\left({\delta }_{\text{r}}\right)$ are $\underset{\_}{0.243\text{mm}}$ and $\underset{\_}{-0.1325\text{mm}}$.

Explanation of Solution

Given information:

The length of the tube (L) is $250\text{mm}$.

The outer diameter of the tube $\left(D_{\text{t}}\right)$ is $36\text{mm}$.

The inner diameter of the tube $\left(d_{\text{t}}\right)$ is $28\text{mm}$.

The Young’s modulus of the aluminium $\left(E_{\text{t}}\right)$ is $70\text{GPa}$.

The diameter of the rod $\left(d_{\text{r}}\right)$ is $25\text{mm}$.

The Young’s modulus of the brass $\left(E_{\text{r}}\right)$ is $105\text{GPa}$.

The pitch of the single-threaded screw-on cover (p) is $1.5\text{mm}$.

The load act in the tube is P.

Calculation:

Calculate the cross sectional area of the tube $\left(A_{\text{t}}\right)$ using the formula:

$A_{\text{t}}=\frac{\pi }{4}\left(D_{\text{t}}^2-d_{\text{t}}^2\right)$

Substitute $36\text{mm}$ for $D_{\text{t}}$ and $28\text{mm}$ for $d_{\text{t}}$.

$\begin{array}{c}{A}_{\text{t}}=\frac{\pi }{4}\times \left({36}^2-{28}^2\right)\\ =402.124{\text{mm}}^2\end{array}$

Calculate the cross sectional area of the rod $\left(A_{\text{r}}\right)$ using the formula:

$A_{\text{r}}=\frac{\pi }{4}{d}_{\text{r}}^2$

Substitute $25\text{mm}$ for $d_{\text{r}}$.

$\begin{array}{c}{A}_{\text{r}}=\frac{\pi }{4}\times {25}^2\\ =490.874{\text{mm}}^2\end{array}$

Calculate the deformation of the tube $\left({\delta }_{\text{t}}\right)$ using the formula:

${\delta }_{\text{t}}=\frac{PL}{A_{\text{t}}{E}_{\text{t}}}$

Substitute $250\text{mm}$ for L, $402.124{\text{mm}}^2$ for $A_{\text{t}}$, and $70\text{GPa}$ for $E_{\text{t}}$.

$\begin{array}{c}{\delta }_{\text{t}}=\frac{P\times 250}{402.124{\text{mm}}^2\times 70\text{GPa}\times \frac{{10}^3{\text{N/mm}}^2}{1\text{GPa}}}\\ =8.8814\times {10}^{-6}P\end{array}$ (1)

Calculate the deformation of the rod $\left({\delta }_{\text{r}}\right)$ using the formula:

${\delta }_{\text{r}}=-\frac{PL}{A_{\text{r}}{E}_{\text{r}}}$

Substitute $250\text{mm}$ for L, $490.874{\text{mm}}^2$ for $A_{\text{r}}$, and $105\text{GPa}$ for $E_{\text{r}}$.

$\begin{array}{c}{\delta }_{\text{r}}=-\frac{P\times 250}{490.874{\text{mm}}^2\times 105\text{GPa}\times \frac{{10}^3{\text{N/mm}}^2}{1\text{GPa}}}\\ =-4.8504\times {10}^{-6}P\end{array}$ (2)

Calculate the deformation of the screw $\left(\delta \right)$ using the formula:

$\delta =\frac{1}{4}p$

Substitute $1.5\text{mm}$ for p.

$\begin{array}{c}\delta =\frac{1}{4}\times 1.5\\ =0.375\text{mm}\end{array}$

Calculate the load (P) act in the tube using the formula:

$\delta ={\delta }_{\text{t}}-{\delta }_{\text{r}}$

Substitute $0.375\text{mm}$ for $\delta$, $-4.8504\times {10}^{-6}P$ for ${\delta }_{\text{r}}$, and $8.8814\times {10}^{-6}P$ for ${\delta }_{\text{t}}$.

$\begin{array}{c}0.375=-4.8504\times {10}^{-6}P-8.8814\times {10}^{-6}P\\ 0.375=1.37318\times {10}^{-5}P\\ P=\frac{0.375}{1.37318\times {10}^{-5}}\\ =27.308\times {10}^3\text{N}\end{array}$

Calculate the deformations of the tube $\left({\delta }_{\text{t}}\right)$:

Substitute $27.308\times {10}^3\text{N}$ for P in Equation (1).

$\begin{array}{c}{\delta }_{\text{t}}=8.8814\times {10}^{-6}\times 27.308\times {10}^3\\ =0.243\text{mm}\end{array}$

Calculate the deformations of the rod $\left({\delta }_{\text{r}}\right)$:

Substitute $27.308\times {10}^3\text{N}$ for P in Equation (2).

$\begin{array}{c}{\delta }_{\text{r}}=-4.8504\times {10}^{-6}\times 27.308\times {10}^3\\ =0.1325\text{mm}\end{array}$

Hence, the deformations of the tube $\left({\delta }_{\text{t}}\right)$ and of the rod $\left({\delta }_{\text{r}}\right)$ are $\underset{\_}{0.243\text{mm}}$ and $\underset{\_}{-0.1325\text{mm}}$.