EBK MECHANICS OF MATERIALS
7th Edition
ISBN: 8220100257063
Author: BEER
Publisher: YUZU
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.3, Problem 56P
Determine the maximum load P that can be applied to the brass bar of Prob. 2.55 if the allowable stress in the steel bars is 30 MPa and the allowable stress in the brass bar is 25 MPa.
2.55 Two steel bars (Es = 200 GPa and αs = 11.7 × 10-6/°C) are used to reinforce a brass bar (Eb = 105 GPa, αb = 20.9 × 10-6/°C) that is subjected to a load P = 25 kN. When the steel bars were fabricated, the distance between the centers of the holes that were to fit on the pins was made 0.5 mm smaller than the 2 m needed. The steel bars were then placed in an oven to increase their length so that they would just fit on the pins. Following fabrication, the temperature in the steel bars dropped back to room temperature. Determine (a) the increase in temperature that was required to fit the steel bars on the pins, (b) the stress in the brass bar after the load is applied to it.
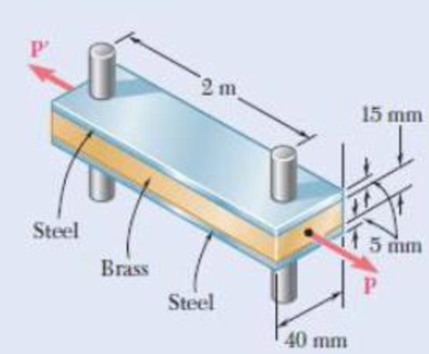
Fig. P2.55
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
At room temperature (20 °C) a 0.8 mm gap exists between the ends of the rods shown. At a later time when the temperature has reached 120 °C, determine (a) the normal stress in the aluminum rod, (b) the change in length of the aluminum rod
4. A rigid block of having a
weight M is suspended by
symmetrically placed rods. Each
copper rod has an area of 1200
sq.mm: E= 125,000 MPa and the
allowable stress is 90 MPa. The
steel rod has an area of 1500
sq.mm; E= 220GPa; and the
allowable stress is 120 Mpa.
Determine the largest weight M
which can be supported by the
rods.
8c = 8s
52 C 280
Copper
160 mm
Pc
Ps
Steel
240 mm
Pc
...initial level
"Tinal level
Copper
160 mm
Question 1: A steel rod is rigidly attached between an aluminum rod and a bronze rod as shown . Axial
loads are applied at the positions indicated. Find the maximum value of P that will not exceed a stress in
steel of 140 MPa, in aluminum of 90 MPa, or in bronze of 100 MPa.
STEEL
A = 400 mm²
ALUMINUM
BRONZE
A = 200 mm²
A = 500 mm²
2P
4P
2.5 m
2.0 m
1.5 m
Chapter 2 Solutions
EBK MECHANICS OF MATERIALS
Ch. 2.1 - A nylon thread is subjected to a 8.5-N tension...Ch. 2.1 - A 4.8-ft-long steel wire of 14 -in.-diameter is...Ch. 2.1 - An 18-m-long steel wire of 5-mm diameter is to be...Ch. 2.1 - Two gage marks are placed exactly 250 mm apart on...Ch. 2.1 - An aluminum pipe must not stretch more than 0.05...Ch. 2.1 - A control rod made of yellow brass must not...Ch. 2.1 - A steel control rod is 5.5 ft long and must not...Ch. 2.1 - A cast-iron tube is used to support a compressive...Ch. 2.1 - A 4-m-long steel rod must not stretch more than 3...Ch. 2.1 - A nylon thread is to be subjected to a 10-N...
Ch. 2.1 - A block of 10-in. length and 1.8 1.6-in. cross...Ch. 2.1 - A square yellow-brass bar must not stretch more...Ch. 2.1 - Rod BD is made of steel (E = 29 106 psi) and is...Ch. 2.1 - The 4-mm-diameter cable BC is made of a steel with...Ch. 2.1 - A single axial load of magnitude P = 15 kips is...Ch. 2.1 - A 250-mm-long aluminum tube (E = 70 GPa) of 36-mm...Ch. 2.1 - The specimen shown has been cut from a...Ch. 2.1 - The brass tube AB (E = 105 GPa) has a...Ch. 2.1 - Both portions of the rod ABC are made of an...Ch. 2.1 - The rod ABC is made of an aluminum for which E =...Ch. 2.1 - For the steel truss (E = 200 GPa) and loading...Ch. 2.1 - For the steel truss (E = 29 106 psi) and loading...Ch. 2.1 - Members AB and BC are made of steel (E = 29 106...Ch. 2.1 - The steel frame (E = 200 GPa) shown has a diagonal...Ch. 2.1 - Link BD is made of brass (E = 105 GPa) and has a...Ch. 2.1 - Members ABC and DEF are joined with steel links (E...Ch. 2.1 - Each of the links AB and CD is made of aluminum (E...Ch. 2.1 - The length of the 332-in.-diameter steel wire CD...Ch. 2.1 - A homogenous cable of length L and uniform cross...Ch. 2.1 - The vertical load P is applied at the center A of...Ch. 2.1 - Denoting by the "engineering strain'' in a...Ch. 2.1 - The volume of a tensile specimen is essentially...Ch. 2.3 - An axial centric force of magnitude P = 450 kN is...Ch. 2.3 - An axial centric force of magnitude P = 450 kN is...Ch. 2.3 - The 4.5-ft concrete post is reinforced with six...Ch. 2.3 - The 4.5-ft concrete post is reinforced with six...Ch. 2.3 - An axial force of 200 kW is applied to the...Ch. 2.3 - The length of the assembly shown decreases by 0.40...Ch. 2.3 - A polystyrene rod consisting of two cylindrical...Ch. 2.3 - Three steel rods (E = 29 106 psi) support an...Ch. 2.3 - Fig. P2.41 2.41 Two cylindrical rods, one of steel...Ch. 2.3 - Solve Prob. 2.41, assuming that rod AC is made of...Ch. 2.3 - Each of the rods BD and CE is made of brass (E =...Ch. 2.3 - The rigid bar AD is supported by two steel wires...Ch. 2.3 - The rigid bar ABC is suspended from three wines of...Ch. 2.3 - The rigid bar AD is supported by two steel wires...Ch. 2.3 - The aluminum shell is fully bonded to the brass...Ch. 2.3 - The aluminum shell is fully bonded to the brass...Ch. 2.3 - The brass shell (b = 11.6 10-6/F) is fully bonded...Ch. 2.3 - The concrete post (Ec = 3.6 106) psi and c = 5.5 ...Ch. 2.3 - A rod consisting of two cylindrical portions AB...Ch. 2.3 - A rod consisting of two cylindrical portions AB...Ch. 2.3 - Fig. P2.52 2.52 A rod consisting of two...Ch. 2.3 - The steel rails of a railroad (rack (Es = 200GPa,...Ch. 2.3 - Two steel bars (Es = 200 GPa and s = 11.7 10-6/C)...Ch. 2.3 - Determine the maximum load P that can be applied...Ch. 2.3 - An aluminum rod (Ea = 70 GPa, a = 23.6 10-6/C)...Ch. 2.3 - Knowing that a 0.02-in. gap exists when the...Ch. 2.3 - Determine (a) the compressive force in the bars...Ch. 2.3 - At room temperature (20C) a 0.5-mm gap exists...Ch. 2.9 - A standard tension test is used to determine the...Ch. 2.9 - A 2-m length of an aluminum pipe of 240-nun outer...Ch. 2.9 - A line of slope 4:10 has been scribed on a...Ch. 2.9 - A 2.75-kN tensile load is applied to a test coupon...Ch. 2.9 - Fig. P2.65 2.65 In a standard tensile test a steel...Ch. 2.9 - The change in diameter of a large steel bolt is...Ch. 2.9 - The brass rod AD is fitted with a jacket that is...Ch. 2.9 - A fabric used in air-inflated structures is...Ch. 2.9 - A 1-in. square was scribed on the side of a large...Ch. 2.9 - The block shown is made of a magnesium alloy for...Ch. 2.9 - The homogeneous plate ABCD is subjected to a...Ch. 2.9 - For a member under axial loading, express the...Ch. 2.9 - In many situations it is known that the normal...Ch. 2.9 - In many situations physical constraints prevent...Ch. 2.9 - The plastic block shown is bonded to a rigid...Ch. 2.9 - The plastic block shown is bonded to a rigid...Ch. 2.9 - Two blocks of rubber with a modulus of rigidity G...Ch. 2.9 - Fig. P2.77 and P2.78 2.78 Two blocks of rubber...Ch. 2.9 - An elastomeric bearing (G = 130 psi) is used to...Ch. 2.9 - 2.80 For the elastomeric bearing In Prob. 2.79...Ch. 2.9 - A vibration isolation unit consists of two blocks...Ch. 2.9 - Prob. 82PCh. 2.9 - Prob. 83PCh. 2.9 - Prob. 84PCh. 2.9 - Prob. 85PCh. 2.9 - A 2.75-kN tensile load is applied to a test coupon...Ch. 2.9 - A vibration isolation support consists of a rod A...Ch. 2.9 - Prob. 88PCh. 2.9 - Prob. 89PCh. 2.9 - Show that for any given material, the ratio G/E of...Ch. 2.9 - Prob. 91PCh. 2.9 - Prob. 92PCh. 2.13 - Knowing that, for the plate shown, the allowable...Ch. 2.13 - Knowing that P = 38 kN, determine the maximum...Ch. 2.13 - A hole is to be drilled in the plate at A. The...Ch. 2.13 - Fig. P2.95 and P2.96 2.96 (a) For P = 13 kips and...Ch. 2.13 - 2.97 Knowing that the hole has a diameter of 9 mm,...Ch. 2.13 - For P = 100 kN, determine the minimum plate...Ch. 2.13 - Prob. 99PCh. 2.13 - A centric axial force is applied to the steel bar...Ch. 2.13 - The cylindrical rod AB has a length L = 5 ft and a...Ch. 2.13 - Fig. P2.101 and P.102 2.102 The cylindrical rod AB...Ch. 2.13 - Rod AB is made of a mild steel that is assumed to...Ch. 2.13 - Prob. 104PCh. 2.13 - Rod ABC consists of two cylindrical portions and...Ch. 2.13 - Prob. 106PCh. 2.13 - Prob. 107PCh. 2.13 - Prob. 108PCh. 2.13 - Each cable has a cross-sectional area of 100 mm2...Ch. 2.13 - Prob. 110PCh. 2.13 - Two tempered-steel bars, each 316 in. thick, are...Ch. 2.13 - Prob. 112PCh. 2.13 - Prob. 113PCh. 2.13 - Prob. 114PCh. 2.13 - Prob. 115PCh. 2.13 - Prob. 116PCh. 2.13 - Prob. 117PCh. 2.13 - Prob. 118PCh. 2.13 - Prob. 119PCh. 2.13 - For the composite bar in Prob. 2.111, determine...Ch. 2.13 - Prob. 121PCh. 2.13 - Bar AB has a cross-sectional area of 1200 mm2 and...Ch. 2.13 - Bar AB has a cross-sectional area of 1200 mm2 and...Ch. 2 - The uniform wire ABC, of unstretched length 2l, is...Ch. 2 - The aluminum rod ABC (E = 10.1 106 psi), which...Ch. 2 - Two solid cylindrical rods are joined at B and...Ch. 2 - Prob. 127RPCh. 2 - Prob. 128RPCh. 2 - Prob. 129RPCh. 2 - A 4-ft concrete post is reinforced with four steel...Ch. 2 - The steel rods BE and CD each have a 16-mm...Ch. 2 - Prob. 132RPCh. 2 - Prob. 133RPCh. 2 - The aluminum test specimen shown is subjected to...Ch. 2 - Prob. 135RP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The rigid beam BC is supported by rods (1) and (2). The cross-sectional area of rod (1) is 9 mm². The cross-sectional area of rod (2) is 14 mm². For a uniformly distributed load of w 4.0 kN/m, determine the length a so that the normal stress is the same in each rod. Assume L = 4.50 m. (1) Answer: a = L W a (2) marrow_forwardA 13-mm-diameter steel (E = 193 GPa) rod (2) is connected to a 27-mm-wide by 10-mm-thick rectangular aluminum (E = 72 GPa) bar (1), as shown. Assume L1 = 0.74 m and L2 = 1.38 m. Determine the force P (in kN rounded to the nearest tenths) required to stretch the assembly 8.1 mm.arrow_forwardThe rigid beam BC is supported by rods (1) and (2). The cross-sectional area of rod (1) is 11 mm². The cross-sectional area of rod (2) is 14 mm2. For a uniformly distributed load of w = 4.1 kN/m, determine the length a so that the normal stress is the same in each rod. Assume L = 5.35 m. A (1) (2) a L. Answer: a = i marrow_forward
- Rigid bar ABC supports a weight of W = 26 kN. Bar ABC is pinned at A and supported at B by rod (1), which has a circular cross section. If the normal stress in rod (1) must be limited to 110 MPa, determine the minimum diameter required for the rod. (1) B C 700 mm 350 mmarrow_forwardAxial loads are applied with rigid bearing plates to the solid cylindrical rods shown. The normal stress in aluminum rod (1) must be limited to 19 ksi, the normal stress in brass rod (2) must be limited to 24 ksi, and the normal stress in steel rod (3) must be limited to 12 ksi. Determine the minimum diameter required for each of the three rods. Assume P = 9 kips, Q = 4 kips, R = 18 kips and S = 21 kips. Calculate the internal force (positive if tensile, negative if compresive) in rod (1). Use a FBD cutting through the rod in the section that includes the free end A.Answer: F1 = ? kips.arrow_forwardAxial loads are applied with rigid bearing plates to the solid cylindrical rods shown. The normal stress in aluminum rod (1) must be limited to 19 ksi, the normal stress in brass rod (2) must be limited to 24 ksi, and the normal stress in steel rod (3) must be limited to 12 ksi. Determine the minimum diameter required for each of the three rods. Assume P = 9 kips, Q = 4 kips, R = 18 kips and S = 21 kips.Calculate the internal force (positive if tensile, negative if compresive) in rod (1). Use a FBD cutting through the rod in the section that includes the free end A.arrow_forward
- 4. A steel rod of 3 cm diameter is enclosed centrally in a hollow copper tube of external diameter 5 cm and internal diameter of 4 cm. The composite bar is then subjected to an axial pull of 45 000 N. If the length of each bar is equal to 150 mm. Determine (i) The stress in the rod and tube (ii) Load carried by each bararrow_forwardThe rigid beam BC is supported by rods (1) and (2). The cross-sectional area of rod (1) is 9 mm². The cross-sectional area of rod (2) is 18 mm². For a uniformly distributed load of w = 2.3 kN/m, determine the length a so that the normal stress is the same in each rod. Assume L = 3.00 m. (1) B Answer: a = i L W a (2) marrow_forwardThe rigid beam BC is supported by rods (1) and (2). The cross-sectional area of rod (1) is 10 mm2. The cross-sectional area of rod (2) is 18 mm2. For a uniformly distributed load of w = 2.4 kN/m, determine the length a so that the normal stress is the same in each rod. Assume L = 5.25 m.arrow_forward
- P- 45° 45° Fig. 2-38arrow_forwardA 13-mm-diameter steel (E = 193 GPa) rod (2) is connected to a 27-mm-wide by 10-mm-thick rectangular aluminum (E = 72 GPa) bar (1), as shown. Assume L1 = 0.74 m and L2 = 1.38 m. Determine the force P (in kN rounded to the nearest tenths) required to stretch the assembly 8.1 mm. (1) L₁ B L2 C P ...arrow_forwardTwo solid cylindrical rods support a load of P = 25 kN as shown. Rod (1) has a diameter of 16 mm, and the diameter of rod (2) is 12 mm. Determine the axial stress in rod (1). 5.6 m 3.8 m (1) 91.1 MPa O 121.0 MPa 62.4 MPa 101.1 MPa O 75.5 MPa B 4.6 m 2 3.3 marrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
EVERYTHING on Axial Loading Normal Stress in 10 MINUTES - Mechanics of Materials; Author: Less Boring Lectures;https://www.youtube.com/watch?v=jQ-fNqZWrNg;License: Standard YouTube License, CC-BY