Introduction To Finite Element Analysis And Design
2nd Edition
ISBN: 9781119078722
Author: Kim, Nam H., Sankar, Bhavani V., KUMAR, Ashok V., Author.
Publisher: John Wiley & Sons,
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2, Problem 26E
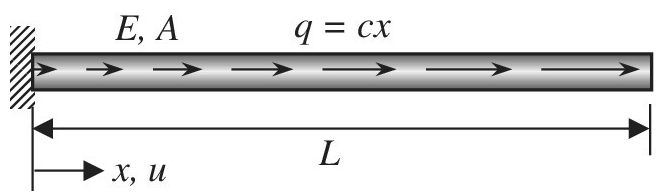
Consider the uniform bar in the figure. Axial load q is linearly distributed along the length of the bar according to
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
My answers are incorrect
Picture
What is the weight of a 5-kg substance in N, kN, kg·m/s², kgf, Ibm-ft/s², and lbf?
The weight of a 5-kg substance in N is 49.05
N.
The weight of a 5-kg substance in kN is
KN.
The weight of a 5-kg substance in kg·m/s² is 49.05
kg-m/s².
The weight of a 5-kg substance in kgf is 5.0 kgf.
The weight of a 5-kg substance in Ibm-ft/s² is 11.02 lbm-ft/s².
The weight of a 5-kg substance in lbf is 11.023
lbf.
Chapter 2 Solutions
Introduction To Finite Element Analysis And Design
Ch. 2 - Answer the following descriptive questions.
a....Ch. 2 - Use the Galerkin method to solve the following...Ch. 2 - Solve the differential equation in problem 2 using...Ch. 2 - Prob. 4ECh. 2 - Using the Galerkin method, solve the following...Ch. 2 - A one-dimensional heat conduction problem can be...Ch. 2 - Solve the one-dimensional heat conduction problem...Ch. 2 - Prob. 8ECh. 2 - Solve the differential equation in problem 8 for...Ch. 2 - Prob. 10E
Ch. 2 - Prob. 11ECh. 2 - Prob. 12ECh. 2 - Using the Galerkin method, calculate the...Ch. 2 - The boundary-value problem for a clamped-clamped...Ch. 2 - The boundary-value problem for a cantilevered beam...Ch. 2 - Prob. 16ECh. 2 - Consider a finite element with three nodes, as...Ch. 2 - A vertical rod of elastic material is fixed at...Ch. 2 - A bar in the figure is under the uniformly...Ch. 2 - Prob. 20ECh. 2 - A tapered bar with circular cross section is fixed...Ch. 2 - The stepped bar shown in the figure is subjected...Ch. 2 - A bar shown in the figure is modeled using three...Ch. 2 - Consider the tapered bar in problem 17. Use the...Ch. 2 - Consider the tapered bar in problem 21. Use the...Ch. 2 - Consider the uniform bar in the figure. Axial load...Ch. 2 - Determine shape functions of a bar element shown...Ch. 2 - Consider a finite element with three nodes, as...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
How is the hydrodynamic entry length defined for flow in a pipe? Is the entry length longer in laminar or turbu...
Fluid Mechanics: Fundamentals and Applications
Represent each force as a Cartesian vector and determine the magnitude and coordinate direction angles of the r...
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
Why are shielded metal arc electrodes often baked just prior to welding?
Degarmo's Materials And Processes In Manufacturing
3.3 It is known that a vertical force of 200 lb is required to remove the nail at C from the board. As the nail...
Vector Mechanics for Engineers: Statics
(Greatest Common Divisor) The greatest common divisor (GCD) of two integers is the largest integer that evenly ...
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
CONCEPT QUESTIONS
15.CQ3 The ball rolls without slipping on the fixed surface as shown. What is the direction ...
Vector Mechanics for Engineers: Statics and Dynamics
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Mych CD 36280 kg. 0.36 givens Tesla truck frailer 2017 Model Vven 96154kph ronge 804,5km Cr Powertrain Across PHVAC rwheel 0.006 0.88 9M² 2 2kW 0.55M ng Zg Prated Trated Pair 20 0.95 1080 kW 1760 Nm 1,2 determine the battery energy required to meet the range when fully loaded determine the approximate time for the fully-loaded truck-trailor to accelerate from 0 to 60 mph while Ignoring vehicle load forcesarrow_forward12-217. The block B is sus- pended from a cable that is at- tached to the block at E, wraps around three pulleys, and is tied to the back of a truck. If the truck starts from rest when ID is zero, and moves forward with a constant acceleration of ap = 0.5 m/s², determine the speed of the block at D the instant x = 2 m. Neglect the size of the pulleys in the calcu- lation. When xƊ = 0, yc = 5 m, so that points C and D are at the Prob. 12-217 5 m yc =2M Xparrow_forwardsolve both and show matlab code auto controlsarrow_forward
- 12-82. The roller coaster car trav- els down the helical path at con- stant speed such that the paramet- ric equations that define its posi- tion are x = c sin kt, y = c cos kt, z = h - bt, where c, h, and b are constants. Determine the mag- nitudes of its velocity and accelera- tion. Prob. 12-82 Narrow_forwardGiven: = refueling Powertran SOURCE EMISSIONS vehide eff eff gasoline 266g co₂/kwh- HEV 0.90 0.285 FLgrid 411ilg Co₂/kWh 41111gCo₂/kWh EV 0.85 0.80 Production 11x10% og CO₂ 13.7 x 10°g CO₂ A) Calculate the breakeven pont (in km driven) for a EV against on HEV in Florida of 0.1kWh/kM Use a drive cycle conversion 5) How efficient would the powertrain of the HEV in this example have to be to break even with an EV in Florida after 150,000 Miles of service (240,000) km Is it plausible to achieve the answer from pert b Consideans the HaXINERY theoretical efficiency of the Carnot cycle is 5020 and there are additional losses of the transMISSION :- 90% efficiency ? c A what do you conclude is the leading factor in why EVs are less emissive than ICE,arrow_forwardsolve autocontrolsarrow_forward
- Problem 3.21P: Air at 100F(38C) db,65F(18C) wb, and sea-level pressure is humidified adiabatically with steam. The steam supplied contains 20 percent moisture(quality of 0.80) at 14.7psia(101.3kpa). The air is humidified to 60 percent relative humidity. Find the dry bulb temperature of the humidified air using (a)chart 1a or 1b and (b) the program PSYCH.arrow_forwardPUNTO 4. calculate their DoF using Gruebler's formula. PUNTO 5. Groundarrow_forwardPUNTO 2. PUNTO 3. calculate their DoF using Gruebler's formula. III IAarrow_forward
- calculate their DoF using Gruebler's formula. PUNTO 6. PUNTO 7. (Ctrl)arrow_forwardA pump delivering 230 lps of water at 30C has a 300-mm diameter suction pipe and a 254-mm diameter discharge pipe as shown in the figure. The suction pipe is 3.5 m long and the discharge pipe is 23 m long, both pipe's materials are cast iron. The water is delivered 16m above the intake water level. Considering head losses in fittings, valves, and major head loss. a) Find the total dynamic head which the pump must supply. b)It the pump mechanical efficiency is 68%, and the motor efficiency is 90%, determine the power rating of the motor in hp.given that: summation of K gate valve = 0.25check valve=390 degree elbow= 0.75foot valve= 0.78arrow_forwardA pump delivering 230 lps of water at 30C has a 300-mm diameter suction pipe and a 254-mm diameter discharge pipe as shown in the figure. The suction pipe is 3.5 m long and the discharge pipe is 23 m long, both pipe's materials are cast iron. The water is delivered 16m above the intake water level. Considering head losses in fittings, valves, and major head loss. a) Find the total dynamic head which the pump must supply. b)It the pump mechanical efficiency is 68%, and the motor efficiency is 90%, determine the power rating of the motor in hp.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Lec21, Part 5, Strain transformation; Author: Mechanics of Materials (Libre);https://www.youtube.com/watch?v=sgJvz5j_ubM;License: Standard Youtube License