Introduction To Finite Element Analysis And Design
2nd Edition
ISBN: 9781119078722
Author: Kim, Nam H., Sankar, Bhavani V., KUMAR, Ashok V., Author.
Publisher: John Wiley & Sons,
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2, Problem 17E
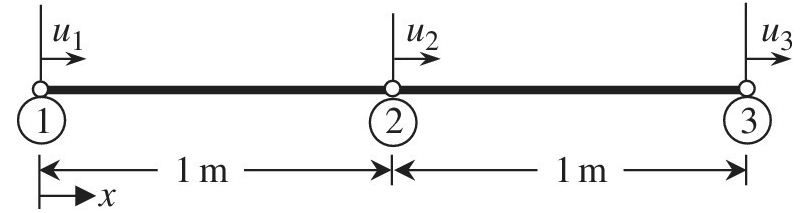
Consider a finite element with three nodes, as shown in the figure. When the solution is approximated using
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Determine by direct integration the moment of inertia of theshaded area at right with respect to the x axis shown.
Determine by direct integration the moment of inertia of theshaded area of the figure with respect to the y axis shown.
For the following MATLAB code, I need to answer a few questions. Can you identify the curves as elliptic functions? Which curves reflect the sn, cn, and dn functions?From the curves, determine the maximum amplitudes and the period corresponding toeach angular velocity component.
clc;
clear all;
I = [500; 125; 425];
w = [0.2; 0.1; 0.2];
rev = 0:0.01:10;
C = eye(3);
% Using ode45 to integrate the KDE and DDE
options = odeset('RelTol',1e-9,'AbsTol',1e-9);
result = ode45(@K_DDE, rev, [w; I; C(:)], options);
v = result.x;
% Extracting information from the ode45 solver
w = result.y(1:3, :);
C_ode = reshape(result.y(7:end, :), [3,3,length(v)]);
plot(v, w)
xlabel('rev')
ylabel('w (rad/s)')
legend('w1', 'w2', 'w3')
% Functions
function dwCdt = K_DDE(~, w_IC)
% Extracting the initial condtions to a variable
w = w_IC(1:3);
I = w_IC(4:6);
C = reshape(w_IC(7:end), [3, 3]);
I1 = I(1);
I2 = I(2);
I3 = I(3);
K1 = -(I3-I2)/I1;
K2 = -(I1-I3)/I2;
K3 = -(I2-I1)/I3;
%…
please show a drawing/image and explain how to properly do the question. thanks
Chapter 2 Solutions
Introduction To Finite Element Analysis And Design
Ch. 2 - Answer the following descriptive questions.
a....Ch. 2 - Use the Galerkin method to solve the following...Ch. 2 - Solve the differential equation in problem 2 using...Ch. 2 - Prob. 4ECh. 2 - Using the Galerkin method, solve the following...Ch. 2 - A one-dimensional heat conduction problem can be...Ch. 2 - Solve the one-dimensional heat conduction problem...Ch. 2 - Prob. 8ECh. 2 - Solve the differential equation in problem 8 for...Ch. 2 - Prob. 10E
Ch. 2 - Prob. 11ECh. 2 - Prob. 12ECh. 2 - Using the Galerkin method, calculate the...Ch. 2 - The boundary-value problem for a clamped-clamped...Ch. 2 - The boundary-value problem for a cantilevered beam...Ch. 2 - Prob. 16ECh. 2 - Consider a finite element with three nodes, as...Ch. 2 - A vertical rod of elastic material is fixed at...Ch. 2 - A bar in the figure is under the uniformly...Ch. 2 - Prob. 20ECh. 2 - A tapered bar with circular cross section is fixed...Ch. 2 - The stepped bar shown in the figure is subjected...Ch. 2 - A bar shown in the figure is modeled using three...Ch. 2 - Consider the tapered bar in problem 17. Use the...Ch. 2 - Consider the tapered bar in problem 21. Use the...Ch. 2 - Consider the uniform bar in the figure. Axial load...Ch. 2 - Determine shape functions of a bar element shown...Ch. 2 - Consider a finite element with three nodes, as...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- For the four-bar- linkage shown in the following figure. BC=68mm, CD=100mm, AD=120mm. Determine the range of AB to make it a crank-rocker mechanism. B Darrow_forwardall of those 4 fi 1)Draw kinematic diagram: 2)DOF: 3)type/name of mechanism 4)evolution:arrow_forward7.4 Impeller viscometer The rheology of a Penicillium chrysogenum broth is examined using an impeller viscometer. The density of the cell suspension is approximately 1000 kg m³. Samples of broth are stirred under laminar conditions using a Rushton turbine of diameter 4 cm in a glass beaker of diameter 15 cm. The average shear rate generated by the impeller is greater than the stirrer speed by a factor of about 10.2. When the stirrer shaft is attached to a device for measuring torque and rotational speed, the following results are recorded. Stirrer speed (s¹) Torque (Nm) 0.185 3.57 × 10-6 0.163 3.45 × 10-6 0.126 3.31 x 10-6 0.111 3.20×10-6 Can the rheology be described using a power-law model? If so, evaluate K and n.arrow_forward
- (read image)arrow_forward(read image) Answer Providedarrow_forwardThis is part B Part A's question and answer was find moment of inertia (Ix = 3.90×10^5) and radius of gyration (kx = 21.861) Determine the centroid ( x & y ) of the I-section, Calculate the moment of inertia of the section about itscentroidal x & y axes. How or why is this result different fromthe result of a previous problem?arrow_forward
- Determine by direct integration the moment of inertia of theshaded area of figure with respect to the y axis shownarrow_forwardConsider the feedback controlled blending system shown below, which is designed to keep theoutlet concentration constant despite potential variations in the stream 1 composition. The density of all streamsis 920 kg/m3. At the nominal steady state, the flow rates of streams 1 and 2 are 950 and 425 kg/min,respectively, the liquid level in the tank is 1.3 m, the incoming mass fractions are x1 = 0.27, x2 = 0.54. Noticethe overflow line, indicating that the liquid level remains constant (i.e. any change in total inlet flow ratetranslates immediately to the same change in the outlet flow rate). You may assume the stream 1 flowrate andthe stream 2 composition are both constant. Use minutes as the time unit throughout this problem. Identify any controlled variable(s) (CVs), manipulated variable(s) (MVs),and disturbance variable(s) (DVs) in this problem. For each, explain how you know that’show it is classified.CVs: ___________, MVs: _____________, DVs: ______________ b) Draw a block diagram…arrow_forwardA heat transfer experiment is conducted on two identical spheres which are initially at the same temperature. The spheres are cooled by placing them in a channel. The fluid velocity in the channel is non-uniform, having a profile as shown. Which sphere cools off more rapidly? Explain. V 1arrow_forward
- My ID# 016948724 last 2 ID# 24 Last 3 ID# 724 Please help to find the correct answer for this problem using my ID# first write le line of action and then help me to find the forces {fx= , fy= mz= and for the last find the moment of inertial about the show x and y axes please show how to solve step by steparrow_forwardMy ID# 016948724 last 2 ID# 24 Last 3 ID# 724 Please help to find the correct answer for this problem using my ID# first write le line of action and then help me to find the forces and the tension {fx= , fy= mz=arrow_forwardMy ID# 016948724 last 2 ID# 24 Last 3 ID# 724 Please help to find the correct answer for this problem using my ID# first write le line of action and then help me to find the forces {fx= , fy= mz=arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Unit Conversion the Easy Way (Dimensional Analysis); Author: ketzbook;https://www.youtube.com/watch?v=HRe1mire4Gc;License: Standard YouTube License, CC-BY