
Concept explainers
The rotating parts of a hydroelectric power plant having power capacity W have a rotational synchronous speed it. The weight of the rotating parts (the hydroturbine and its electric generator) is supported in a thrust bearing having amulet form between D and d diameters as sketched the thrust hearing is operated with a very thin oil film of thickness e and dynamic viscosity. It is armed that the oil is a Newtonian fluid and the velocity is approximated as linear in the hearing. Calculate the ratio of lost power in the thrust heating to the produced power in the hydraulic power plant. Use
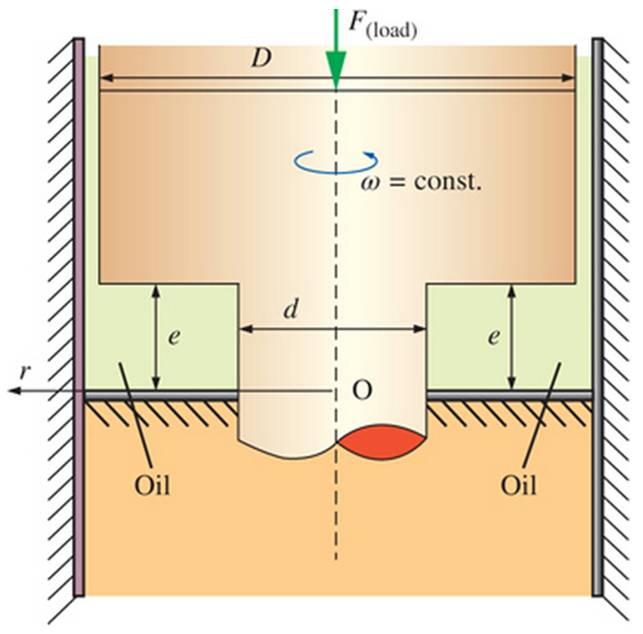
The ratio of lost power in the thrust bearing.
Answer to Problem 127P
The ratio of lost power in the thrust bearing is
Explanation of Solution
Given information:
The larger diameter of the bearing is
Write the expression for the area in differential form.
Here, the area of the plant is
Write the expression for the radius of the smaller bearing.
Here, the radius of the smaller bearing is
Write the expression for the radius of the larger bearing.
Here, the radius of the larger bearing is
Write the expression for the volume of the plant in differential form.
Here, the volume of the plant is
Write the expression for the angular velocity.
Here, the speed of the plant is
Write the expression for the shear stress due to viscosity.
Here, the shear stress due to viscosity is
Write the expression for the force due to shear stress.
Here, the force due to shear stress is
Write the expression for the power loss due to viscosity of oil.
Here, the power loss is
Write the expression for the net power produced.
Here, the net power produced is
Write the expression for the ratio of power loss.
Here, the ratio of power loss is
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Integrate Equation (XIII) under the lower limit
Substitute
Integrate Equation (XIV) under the lower limit
Substitute
Substitute
Integrate Equation (XVI) under the lower limit
Substitute
Substitute
Conclusion:
The ratio of lost power in the thrust bearing is
Want to see more full solutions like this?
Chapter 2 Solutions
Fluid Mechanics: Fundamentals and Applications
- Problem 3.21P: Air at 100F(38C) db,65F(18C) wb, and sea-level pressure is humidified adiabatically with steam. The steam supplied contains 20 percent moisture(quality of 0.80) at 14.7psia(101.3kpa). The air is humidified to 60 percent relative humidity. Find the dry bulb temperature of the humidified air using (a)chart 1a or 1b and (b) the program PSYCH.arrow_forwardPUNTO 4. calculate their DoF using Gruebler's formula. PUNTO 5. Groundarrow_forwardPUNTO 2. PUNTO 3. calculate their DoF using Gruebler's formula. III IAarrow_forward
- calculate their DoF using Gruebler's formula. PUNTO 6. PUNTO 7. (Ctrl)arrow_forwardA pump delivering 230 lps of water at 30C has a 300-mm diameter suction pipe and a 254-mm diameter discharge pipe as shown in the figure. The suction pipe is 3.5 m long and the discharge pipe is 23 m long, both pipe's materials are cast iron. The water is delivered 16m above the intake water level. Considering head losses in fittings, valves, and major head loss. a) Find the total dynamic head which the pump must supply. b)It the pump mechanical efficiency is 68%, and the motor efficiency is 90%, determine the power rating of the motor in hp.given that: summation of K gate valve = 0.25check valve=390 degree elbow= 0.75foot valve= 0.78arrow_forwardA pump delivering 230 lps of water at 30C has a 300-mm diameter suction pipe and a 254-mm diameter discharge pipe as shown in the figure. The suction pipe is 3.5 m long and the discharge pipe is 23 m long, both pipe's materials are cast iron. The water is delivered 16m above the intake water level. Considering head losses in fittings, valves, and major head loss. a) Find the total dynamic head which the pump must supply. b)It the pump mechanical efficiency is 68%, and the motor efficiency is 90%, determine the power rating of the motor in hp.arrow_forward
- The tensile 0.2 percent offset yield strength of AISI 1137 cold-drawn steel bars up to 1 inch in diameter from 2 mills and 25 heats is reported as follows: Sy 93 95 101 f 97 99 107 109 111 19 25 38 17 12 10 5 4 103 105 4 2 where Sy is the class midpoint in kpsi and fis the number in each class. Presuming the distribution is normal, determine the yield strength exceeded by 99.0% of the population. The yield strength exceeded by 99.0% of the population is kpsi.arrow_forwardSolve this problem and show all of the workarrow_forwardI tried to go through this problem but I don't know what I'm doing wrong can you help me?arrow_forward
- Generate the kinematic diagram of the following mechanisms using the given symbols. Then, draw their graphs and calculate their degrees of freedom (DoF) using Gruebler's formula. PUNTO 2. PUNTO 3. !!!arrow_forwardCreate a schematic representation of the following mechanisms using the given symbols and draw their graphs. Then, calculate their degrees of freedom (DoF) using Gruebler's formula. PUNTO 6. PUNTO 7.arrow_forwardhow the kinematic diagram of the following mechanisms would be represented using the given symbols? PUNTO 0. PUNTO 1. °arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





