
Concept explainers
(a)
Interpretation:
The percentage of atoms having velocity within
Concept introduction:
The probability distribution function of the velocities of the gas molecules in each dimension is given by
The Maxwell-Boltzmann distribution is shown below.
This distribution depends on the mass of the particle and absolute temperature.
Answer to Problem 19.73E
The percentage of atoms having a velocity within
Explanation of Solution
The given temperature is
The molar mass of the helium gas is
The graph of
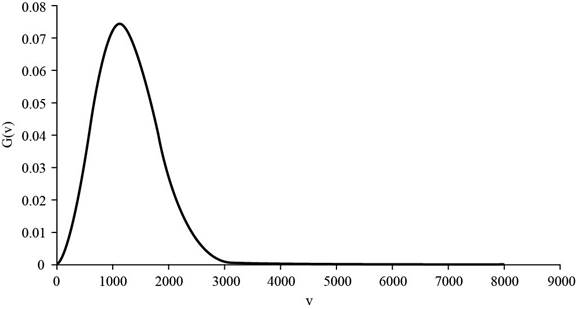
Figure 1
The formula to calculate the root-mean-square speed is given below.
Where,
•
•
•
Substitute the values the value of the molar mass of helium,
The corresponding value of the percentage of atoms having

Figure 2
Therefore, the percentage of atoms having velocity within
The percentage of atoms having velocity within
(b)
Interpretation:
The percentage of atoms having velocity within
Concept introduction:
The probability distribution function of the velocities of the gas molecules in each dimension is given by
The Maxwell-Boltzmann distribution is given by,
This distribution depends on the mass of the particle and absolute temperature.
Answer to Problem 19.73E
The percentage of atoms having velocity within
Explanation of Solution
The given temperature is
The molar mass of the helium gas is
The graph of
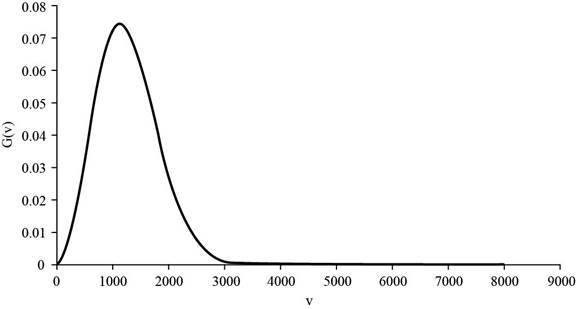
Figure 1
The formula to calculate the most probable speed is given below as,
Where,
•
•
•
Substitute the values the value of the molar mass of helium,
The corresponding value of the percentage of atoms having
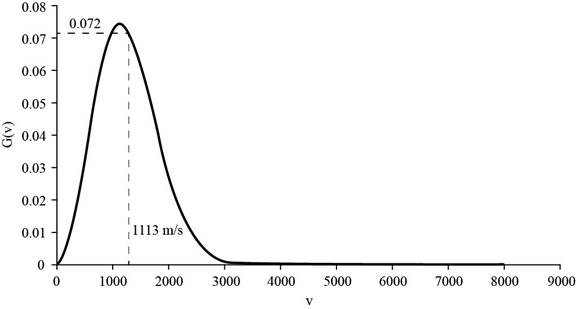
Figure 3
Therefore, the percentage of atoms having velocity within
The percentage of atoms having velocity within
(c)
Interpretation:
The percentage of atoms having velocity within
Concept introduction:
The probability distribution function of the velocities of the gas molecules in each dimension is given by
The Maxwell-Boltzmann distribution is given by,
This distribution depends on the mass of the particle and absolute temperature.
Answer to Problem 19.73E
The percentage of atoms having velocity within
Explanation of Solution
The given temperature is
The molar mass of the helium gas is
The graph of
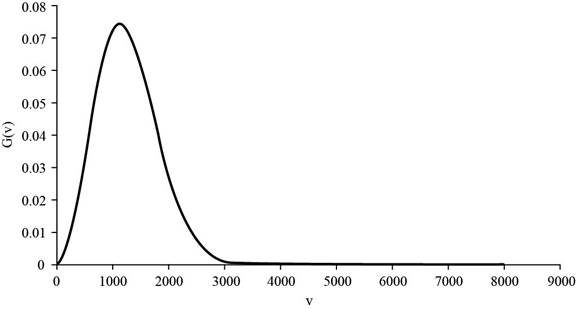
Figure 1
The formula to calculate the mean speed is given below as,
Where,
•
•
•
Substitute the values the value of molar mass of helium,
The corresponding value of percentage of atoms having
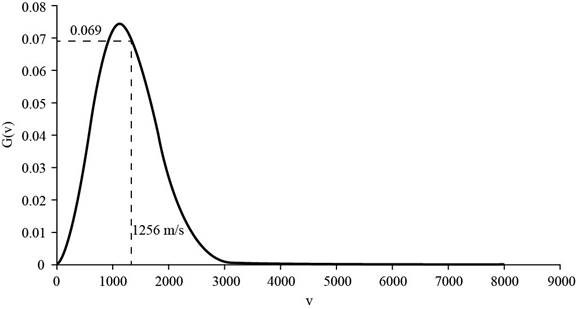
Figure 4
Therefore, the percentage of atoms having velocity within
The percentage of atoms having velocity within
The percentage of atoms having velocity within
Therefore, all the percentages have a relative same value.
The percentage of atoms having velocity within
Want to see more full solutions like this?
Chapter 19 Solutions
Physical Chemistry
- pls help asaparrow_forwardpls help asaparrow_forward9. Consider the following galvanic cell: Fe (s) | Fe(NO3)2 (aq) || Sn(NO3)2 (aq) | Sn (s) a. Write an equation for the half reactions occurring at the anode and cathode. b. Calculate the standard cell potential Show all of your work. c. Draw and label the galvanic cell, including the anode and cathode, direction of electron flow, and direction of ion migration.arrow_forward
- pls help asaparrow_forward11. Use the equation below to answer the following questions: 2 Al(s) + 3 Cd(NO3)2 (aq) → 2 Al(NO3)3 (aq) + 3 Cd(s) a. What is the net ionic equation for the reaction? b. Which species is a spectator ion in this reaction? Define a spectator ion. c. Identify the oxidizing agent and the reducing agent.arrow_forwardpls help asaparrow_forward
- 22arrow_forwardPLEASE READ!!! I DONT WANT EXAMPLES, I DONT WANT WORDS OR PARAGRAPHS FOR THE MECHANISM!!! THANKS First image: QUESTION 6. I have to show, with ARROWS and STRUCTURES, the mechanism of the reaction at the bottom. Also I have to show by mecanism why the reaction wouldn't work if the alcohol was primary. I also tried to draw the mechanism, tell me what to change. Please note that its an AMIDE thats formed not an AMINE the nitrogen has ONE hydrogen and one Phenyl-C-Phenyl. I already asked for this mechanism and got as a final product ...-NH2 not whats shown on the picture, thank you Ths second part. QUESTION 3. I just need a way to synthesize the lactone A, I already started please continue from where I left it Second image: I simply need the products, substrates or reagents, thank youarrow_forwardIndicate how to prepare a 10% sodium hydroxide (NaOH) solution to a slightly alkaline pH.arrow_forward
 Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
 Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage LearningChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage LearningChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co





