Chapter 18.2, Problem 18.104P

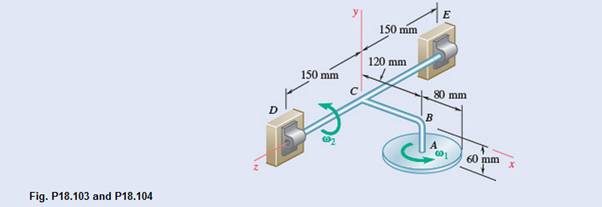
A 2.5-kg homogeneous disk of radius 80 mm rotates at the constant rate ${\omega }_1=50$ rad/s with respect to arm ABC, which is welded to a shaft DCE. Knowing that at the instant shaft DCE has an angular velocity ${\omega }_2=\left(12\text{rad}/\text{s}\right)\text{k}$ and an angular acceleration $a_2=\left(8\text{rad}/{\text{s}}^2\right)\text{k}$ , determine (a) the couple that must be applied to shaft DCE to produce that acceleration, (b) the corresponding dynamic reactions at D and E.

  

To determine

(a)

The couple applied to shaft to produce acceleration.

Answer to Problem 18.104P

The couple applied to shaft to produce acceleration is $0.392\text{N}\cdot \text{m}$ .

Explanation of Solution

Given information:

Mass of homogeneous disk is $2.5\text{Kg}$, angular velocity of disk in y-direction is $50\text{rad}/\text{s}$, radius of the disk is $80\text{mm}$, and length of $DC$ member is $150\text{mm}$.

The figure is represented below.

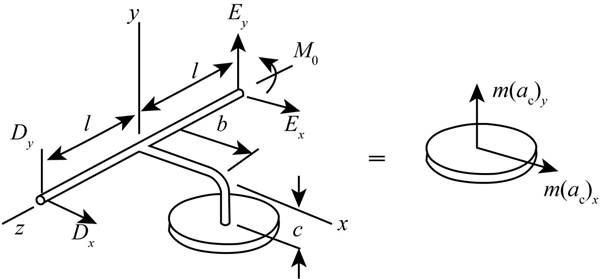
Figure (1)

Write the expression for the angular velocity of disk in x direction.

${\omega }_x=0$   ....... (1)

Write the expression for the total angular velocity of the disk $A$.

$\omega ={\omega }_x\cdot i+{\omega }_y\cdot j{+}_z{\omega }_z\cdot k$   ....... (2)

Here ${\omega }_x$ is angular velocity of disk in x-direction, ${\omega }_y$ is angular velocity of disk in y-direction, ${\omega }_z$ is angular velocity of disk in z-direction.

Substitute, $0$ for ${\omega }_x$, ${\omega }_1$ for ${\omega }_y$ and ${\omega }_1$ for ${\omega }_z$ in equation (2)

$\omega ={\omega }_{1}j+{\omega }_{2}k$   ....... (3)

Write the expression for the angular momentum about point $A$.

${\text{H}}_A={\overline{I}}_x{\omega }_x\cdot i+{\overline{I}}_y{\omega }_y\cdot j+{\overline{I}}_z{\omega }_z\cdot k$   ....... (4)

Here, mass moment of inertia about the x-axis is ${\overline{I}}_x$, mass moment of inertia about the y-axis is ${\overline{I}}_y$, mass moment of inertia about the z-axis is ${\overline{I}}_z$, angular velocity of disk about x axis is ${\omega }_x$, angular velocity of disk about y axis is ${\omega }_y$ .and angular velocity of disk about z axis is ${\omega }_z$.

Substitute $0$ for ${\omega }_x$, ${\omega }_1$ for ${\omega }_y$, and ${\omega }_2$ for ${\omega }_z$ .in Equation (4).

$\begin{array}{c}{\text{H}}_A={\overline{I}}_x\times 0\times \cdot i+{\overline{I}}_y{\omega }_1\cdot j+{\overline{I}}_z{\omega }_2\cdot k\\ {\text{H}}_A={\overline{I}}_y{\omega }_1\cdot j+{\overline{I}}_z{\omega }_{2}k\end{array}$   ....... (6).

Write the expression for angular velocity in vector form of shaft $DCE$ and $CBA$.

$\Omega ={\omega }_{2}k$.   ........ (7)

Write the expression for rate of angular velocity of the reference frame $A_{xyz}$.

${\left({\text{<mover accent="’true'"><mo>H</mo><mo>˙</mo></mover>}}_A\right)}_{xyz}={\overline{I}}_y{\dot{\omega }}_1\cdot j+{\overline{I}}_z{\dot{\omega }}_2\cdot k$   ....... (8)

Here, ${\dot{\omega }}_1$ is rate of angular velocity in y-direction and ${\dot{\omega }}_2$ is rate of angular velocity in z-direction.

Write the expression for rate of total angular velocity.

${\text{<mover accent="’true'"><mo>H</mo><mo>˙</mo></mover>}}_A={\left(\text{<mover accent="’true'"><mo>H</mo><mo>˙</mo></mover>}\right)}_{Ax\text{'}y\text{'}z\text{'}}+\Omega \times {\text{H}}_A$   ....... (9)

Substitute $\left({\overline{I}}_y{\omega }_1\cdot j+{\overline{I}}_z{\omega }_{2}k\right)$ for ${\text{H}}_A$, ${\overline{I}}_y{\dot{\omega }}_1\cdot j+{\overline{I}}_z{\dot{\omega }}_2\cdot k$ for ${\left({\text{<mover accent="’true'"><mo>H</mo><mo>˙</mo></mover>}}_A\right)}_{xyz}$ and ${\omega }_{2}k$ for $\Omega$ in Equation (9).

${\text{<mover accent="’true'"><mo>H</mo><mo>˙</mo></mover>}}_A={\overline{I}}_y{\dot{\omega }}_1\cdot j+{\overline{I}}_z{\dot{\omega }}_2\cdot k+{\omega }_{2}k\times \left(\left({\overline{I}}_y{\omega }_1\cdot j+{\overline{I}}_z{\omega }_{2}k\right)\right)$   ....... (10)

Write the expression for Matrix multiplication of the vector product for Equation (10).

$\begin{array}{c}{\text{<mover accent="’true'"><mo>H</mo><mo>˙</mo></mover>}}_A=\left({\overline{I}}_y{\dot{\omega }}_1\cdot j+{\overline{I}}_z{\dot{\omega }}_2\cdot k\right)+{\overline{I}}_z{\omega }_1{\omega }_{2}i\\ =-{\overline{I}}_y{\omega }_1{\omega }_{2}i+{\overline{I}}_y{\dot{\omega }}_1\cdot j+{\overline{I}}_z{\dot{\omega }}_2\cdot k\end{array}$   ....... (11)

Write the expression for the mass moment of inertia about the y-direction.

${\overline{I}}_y=\frac{1}{2}m{r}^2$   ....... (12)

Here mass of the disk is $m$ and radius of the disk is $r$.

Write the expression for the mass moment of inertia about the z- direction.

${\overline{I}}_z=\frac{1}{4}m{r}^2$   ....... (13)

Substitute $\frac{1}{2}m{r}^2$ for ${\overline{I}}_y$ and $\frac{1}{4}m{r}^2$ for ${\overline{I}}_z$ in Equation (9).

${\text{<mover accent="’true'"><mo>H</mo><mo>˙</mo></mover>}}_A=-\frac{1}{2}m{r}^2{\omega }_1{\omega }_{2}i+\frac{1}{2}m{r}^2{\dot{\omega }}_1\cdot j+\frac{1}{4}m{r}^2{\dot{\omega }}_2\cdot k$   ....... (14)

Write the expression for the velocity of mass centre of the disk.

$v_A={\omega }_{2}k\times r_{A/C}$   ....... (15)

Here, velocity of mass centre is $v_A$ and distance between $C$ and $A$ is $r_{A/C}$.

Write the expression for $r_{A/C}$.

$r_{A/C}=\left(bi-cj\right)$   ....... (16)

Here, horizontal distance is $b$ and vertical distance is $c$.

Substitute $\left(bi-cj\right)$ for $r_{A/C}$ in equation (15)

$v_A={\omega }_{2}k\times \left(bi-cj\right)$ (17)

Write the expression for the matrix multiplication of the vector product for Equation (17).

$v_A=c{\omega }_{2}i+b{\omega }_{2}k$   ....... (18)

Write the expression for the acceleration of the mass centre of the disk.

$a_A={\dot{\omega }}_{2}k\times r_{A/C}+{\omega }_{2}k\times v_A$   ....... (19)

Substitute $\left(bi-cj\right)$ for $r_{A/C}$ and ${\omega }_{2}k\times \left(bi-cj\right)$ for $v_A$

$a_A={\dot{\omega }}_{2}k\times \left(bi-cj\right)+{\omega }_{2}k\times {\omega }_{2}k\times \left(bi-cj\right)$   ....... (20)

Write the expression for the matrix multiplication of the vector product for Equation (20).

$a_A=\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)i+\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)j$   ....... (21)

Write the expression for the the sum of the forces acting on the system.

$F={\text{D}}_{x}i+{\text{D}}_{y}j+E_{x}i+E_{y}j$   ....... (22)

Here, force at $D$ in x-direction is $D_x$, force at $D$ in -direction is $D_y$. force at $E$ in x-direction is $E_x$, and force at $E$ in y-direction is $E_y$.

Write the expression for the force in terms of mass and acceleration.

$F=m{a}_A$   ....... (23)

Substitute ${\text{D}}_{x}i+{\text{D}}_{y}j+E_{x}i+E_{y}j$ for $F$ in Equation (18).

${\text{D}}_{x}i+{\text{D}}_{y}j+E_{x}i+E_{y}j\text{=m}{\text{a}}_A$   ....... (24)

Substitute $\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)i+\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)j$ for $a_A$ in Equation (24)

$\begin{array}{c}{\text{D}}_{x}i+{\text{D}}_{y}j+E_{x}i+E_{y}j\text{=m}\left[\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)i+\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)j\right]\\ \left({\text{D}}_x+E_x\right)i+\left({\text{D}}_y+E_y\right)j=\text{m}\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)i+\text{m}\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)j\end{array}$   ....... (25)

Compare the coefficients of the unit vector of $i$ on both side of Equation (25).

${\text{D}}_x+E_x=\text{m}\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)$   ........ (26)

Compare the coefficients of the unit vector of $i$ on both side of Equation.

${\text{D}}_y{\text{+E}}_y=\text{m}\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)$   ....... (27)

Write the expression for the rate of angular momentum about $E$.

${\dot{H}}_E={\dot{H}}_A+r_{A/E}\times m{a}_A$   ....... (28)

Here, distance of $E$ with respect to $A$ is $r_{A/E}$.

Write the expression for $r_{A/E}$ in vector form.

$r_{A/E}=bi-cj+lk$   ....... (29)

Here distance from point $A$ to $E$ in figure is $l$.

Substitute $-\frac{1}{2}m{r}^2{\omega }_1{\omega }_{2}i+\frac{1}{2}m{r}^2{\dot{\omega }}_1\cdot j+\frac{1}{4}m{r}^2{\dot{\omega }}_2\cdot k$ for ${\dot{H}}_A$, $bi-cj+lk$ for $r_{A/E}$ and $\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)i+\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)j$ for $a_A$ in Equation(28).

${\dot{H}}_E=\left(\begin{array}{l}-\frac{1}{2}m{r}^2{\omega }_1{\omega }_{2}i\\ +\frac{1}{2}m{r}^2{\dot{\omega }}_1\cdot j\\ +\frac{1}{4}m{r}^2{\dot{\omega }}_2\cdot k\end{array}\right)+\frac{1}{4}m{r}^2{\dot{\omega }}_2\cdot k+\left(bi-cj+lk\right)\times m\left(\begin{array}{l}\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)i\\ +\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)j\end{array}\right)$   ....... (30)

Write the expression for the matrix multiplication for vector product for equation (30).

$\begin{array}{c}{\dot{H}}_E=\left[\begin{array}{c}-\frac{1}{2}m{r}^2\times {\omega }_1{\omega }_{2}i+\frac{1}{2}m{r}^2\times {\dot{\omega }}_1\cdot j\\ +\frac{1}{4}m{r}^2\times {\dot{\omega }}_2\cdot k+\left(-lm\right)\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)i\\ +lm\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)j+bm\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)k\\ +cm\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)k\end{array}\right]\\ {\dot{H}}_D=\left[\begin{array}{c}m\left(-\frac{1}{2}{r}^2{\omega }_1{\omega }_2-bl{\dot{\omega }}_2-cl{\omega }_2^2\right)i\\ +m\left(\frac{1}{4}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_1-bl{\omega }_2^2\right){\dot{\omega }}_{2}j\\ +m\left(\frac{1}{4}{r}^2+b^2+c^2\right){\dot{\omega }}_{2}k\end{array}\right]\end{array}$   ....... (31)

Write the expression for the moment about $E$

$M_E=M_{0}k+2lk\times \left(D_{x}i+D_{y}j\right)$   ....... (32)

Here, moment couple when system is at rest is $M_0$.

Write the expression for the matrix multiplication for the vector product for equation (32).

$M_E=-2l{D}_{y}i+2l{D}_{x}j+M_{0}k$   ....... (33)

The sum of the moment at $D$ is equal to the rate of change of angular momentum at $E$.

$M_E={\dot{H}}_D$   ....... (34)

Substitute $M_E=-2l{D}_{y}i+2l{D}_{x}j+M_{0}k$ for $M_E$ in equation (25).

$\left[\begin{array}{l}-2l{D}_{y}i\\ +2l{D}_{x}j\\ +M_{0}k\end{array}\right]=\left[\begin{array}{c}m\left(-\frac{1}{2}{r}^2{\omega }_1{\omega }_2-bl{\dot{\omega }}_2-cl{\omega }_2^2\right)i\\ +m\left(\frac{1}{4}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_2-bl{\omega }_2^2\right)j\\ +m\left(\frac{1}{4}{r}^2+b^2+c^2\right){\dot{\omega }}_{2}k\end{array}\right]$   ....... (30)

Compare the coefficients of the unit vector of $k$ on both side of Equation (30).

$M_0=m\left(\frac{1}{4}{r}^2+b^2+c^2\right){\dot{\omega }}_2$   ....... (31)

Calculation:

Substitute values of $2.5\text{kg}$ for $m$, $\left(80\text{mm}\right)$ for $r$, $\left(120\text{mm}\right)$ for $b$, $60\text{mm}$ for $c$ and $8\text{rad}/{\text{s}}^2$ for ${\dot{\omega }}_2$ in Equation (31).

$\begin{array}{c}{M}_0=2.5\text{kg}\left(\frac{1}{4}{\left(80\text{mm}\right)}^2+{\left(120\text{mm}\right)}^2+{\left(60\text{mm}\right)}^2\right)\left(8\text{rad}/{\text{s}}^2\right)\\ M_0=2.5\text{kg}\left(\begin{array}{l}\frac{1}{4}{\left(80\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)}^2\\ +{\left(120\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)}^2\\ +{\left(60\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)}^2\end{array}\right)\left(8\text{rad}/{\text{s}}^2\right)\\ =0.392\text{N}\cdot \text{m}\end{array}$

Thus value of couple $M_0$ is $0.392\text{N}\cdot \text{m}$.

Conclusion:

The couple applied to shaft to produce acceleration is $0.392\text{N}\cdot \text{m}$.

To determine

(b)

The dynamic reaction at $D$

The dynamic reaction at $E$.

Answer to Problem 18.104P

The dynamic reactions at $D$ is $\left(-21\text{N}\right)i+\left(28\text{N}\right)j$.

The dynamic reactions at $E$ is $\left(-21\text{N}\right)i+\left(-4\text{N}\right)j$.

Explanation of Solution

Given information:

Compare the coefficients of the unit vector of $j$ on both side of Equation (30).

$\begin{array}{c}2l{D}_x=m\left(\frac{1}{4}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_2-bl{\omega }_2^2\right)\\ D_x=\frac{m}{2l}\left(\frac{1}{4}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_2-bl{\omega }_2^2\right)\end{array}$   ....... (32).

Compare the coefficients of the unit vector of $i$ on both side of Equation (30).

$\begin{array}{c}-2l{D}_y=m\left(-\frac{1}{2}{r}^2{\omega }_1{\omega }_2-bl{\dot{\omega }}_2-cl{\omega }_2^2\right)\frac{\pi }{2}\\ D_y=\frac{m}{2l}\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2+bl{\dot{\omega }}_2+cl{\omega }_2^2\right)\end{array}$   ....... (33)

Substitute $\frac{m}{2l}\left(\frac{1}{4}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_2-bl{\omega }_2^2\right)$ for $D_x$ in Equation (21).

$\begin{array}{l}\left[\begin{array}{l}\frac{m}{2l}\left(\frac{1}{4}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_2-bl{\omega }_2^2\right)\\ +E_x\end{array}\right]=\text{m}\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)\\ E_x=\text{m}\left(c{\dot{\omega }}_2-b{\omega }_2^2\right)-\left[\frac{m}{2l}\left(\frac{1}{4}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_2-bl{\omega }_2^2\right)\right]\\ E_x=\frac{m}{2l}\left(-\frac{1}{2}{r}^2{\dot{\omega }}_1+cl{\dot{\omega }}_2-bl{\omega }_2^2\right)\end{array}$   ....... (34)

Substitute $\frac{m}{2l}\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2+bl{\dot{\omega }}_2+cl{\omega }_2^2\right)$ for $D_y$ in Equation (22).

$\begin{array}{l}\left[\begin{array}{l}\frac{m}{2l}\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2+bl{\dot{\omega }}_2+cl{\omega }_2^2\right)\\ +E_y\end{array}\right]=\text{m}\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)\\ E_y=\text{m}\left(b{\dot{\omega }}_2+c{\omega }_2^2\right)-\left[\frac{m}{2l}\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2+bl{\dot{\omega }}_2+cl{\omega }_2^2\right)\right]\\ E_y=\frac{m}{2l}\left(-\frac{1}{2}{r}^2{\omega }_1{\omega }_2+bl{\dot{\omega }}_2+cl{\omega }_2^2\right)\end{array}$   ....... (35)

Write the expression for the angular velocity in terms of time in y-direction.

${\omega }_2=\left(12\text{rad}/\text{s}\right)k$   ....... (36)

Write the expression for the angular velocity in terms of time in y-direction

${\alpha }_2=\left(8\text{rad}/{\text{s}}^2\right)k$ ...... (37)

Calculation:

Substitute values of $2.5\text{kg}$ for $m$, $\left(80\text{mm}\right)$ for $r$, $\left(120\text{mm}\right)$ for $b$, $60\text{mm}$ for $c$, $\left(150\text{mm}\right)$ for $l$, $50\text{rad}/\text{s}$ for ${\omega }_1$, $0$ for ${\dot{\omega }}_1$, $12\text{rad}/\text{s}$ for ${\omega }_2$ ,and $8\text{rad}/{\text{s}}^2$ for ${\dot{\omega }}_2$ in Equation (34).

$\begin{array}{l}{D}_x=\frac{2.5\text{kg}}{2\left(150\text{mm}\right)}\left(\begin{array}{l}\frac{1}{4}{\left(80\text{mm}\right)}^2\times 0\\ +\left(60\text{mm}\right)\left(150\text{mm}\right)\left(8\text{rad}/{\text{s}}^2\right)\\ -\left(120\text{mm}\right)\left(150\text{mm}\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)\\ D_x=\left[\begin{array}{l}\frac{2.5\text{kg}}{2\left(150\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)}\\ \times \left(\begin{array}{l}\frac{1}{4}{\left(80\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)}^2\times 0\\ +\left(60\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\left(150\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\left(8\text{rad}/{\text{s}}^2\right)\\ -\left(120\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\left(150\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)\end{array}\right]\\ D_x=-21\text{N}\end{array}$

Substitute values of $2.5\text{kg}$ for $m$, $\left(80\text{mm}\right)$ for $r$, $\left(120\text{mm}\right)$ for $b$, $60\text{mm}$ for $c$, $\left(150\text{mm}\right)$ for $l$, $50\text{rad}/\text{s}$ for ${\omega }_1$, $12\text{rad}/\text{s}$ for ${\omega }_2$ ,and $8\text{rad}/{\text{s}}^2$ for ${\dot{\omega }}_2$ in Equation (32).

$D_y=\frac{2.5\text{kg}}{2\left(150\text{mm}\right)}\times \left(\begin{array}{l}\frac{1}{2}{\left(80\text{mm}\right)}^2\left(50\text{rad}/\text{s}\right)\left(12\text{rad}/\text{s}\right)\\ +\left(120\text{mm}\right)\left(150\text{mm}\right)\left(8\text{rad}/{\text{s}}^2\right)\\ +\left(60\text{mm}\right)\left(150\text{mm}\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)$

$D_y=\frac{2.5\text{kg}}{2\left(150\text{mm}\right)}\times \left(\begin{array}{l}\frac{1}{2}{\left(80\text{mm}\right)}^2\left(50\text{rad}/\text{s}\right)\left(12\text{rad}/\text{s}\right)\\ +\left(120\text{mm}\right)\left(150\text{mm}\right)\left(8\text{rad}/{\text{s}}^2\right)\\ +\left(60\text{mm}\right)\left(150\text{mm}\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)$

$D_y=\frac{2.5\text{kg}}{2\left(150\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)}\times \left(\begin{array}{l}\frac{1}{2}{\left(80\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)}^2\left(50\text{rad}/\text{s}\right)\left(12\text{rad}/\text{s}\right)\\ +\left(120\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\left(150\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\left(8\text{rad}/{\text{s}}^2\right)\\ +\left(60\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\left(150\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)$

$D_y=28\text{N}$

Hence, dynamic reaction at $D$ is $\left(-21\text{N}\right)i+\left(28\text{N}\right)j$.

Substitute values of $2.5\text{kg}$ for $m$, $\left(80\text{mm}\right)$ for $r$, $\left(120\text{mm}\right)$ for $b$, $60\text{mm}$ for $c$, $\left(150\text{mm}\right)$ for $l$, $50\text{rad}/\text{s}$ for ${\omega }_1$, $12\text{rad}/\text{s}$ for ${\omega }_2$ ,and $8\text{rad}/{\text{s}}^2$ for ${\dot{\omega }}_2$ in Equation (32).

$\begin{array}{l}{E}_x=\frac{2.5\text{kg}}{2\left(150\text{mm}\right)}\left(\begin{array}{l}-\frac{1}{2}{\left(80\text{mm}\right)}^2\times 0\\ +\left(60\text{mm}\right)\left(150\text{mm}\right)\times 8\text{rad}/{\text{s}}^2\\ -\left(120\text{mm}\right)\left(150\text{mm}\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)\\ E_x=\frac{2.5\text{kg}}{2\left(150\text{mm}\right)}\left(\begin{array}{l}-\frac{1}{2}{\left(80\text{mm}\right)}^2\times 0\\ +\left(60\text{mm}\right)\left(150\text{mm}\right)\times 8\text{rad}/{\text{s}}^2\\ -\left(120\text{mm}\right)\left(150\text{mm}\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)\\ E_x=-21\text{N}\end{array}$

Substitute values of $2.5\text{kg}$ for $m$, $\left(80\text{mm}\right)$ for $r$, $\left(120\text{mm}\right)$ for $b$, $60\text{mm}$ for $c$, $\left(150\text{mm}\right)$ for $l$, $50\text{rad}/\text{s}$ for ${\omega }_1$, $12\text{rad}/\text{s}$ for ${\omega }_2$ ,and $8\text{rad}/{\text{s}}^2$ for ${\dot{\omega }}_2$ in Equation (32).

$\begin{array}{l}{E}_y=\frac{2.5\text{kg}}{2\left(150\text{mm}\right)}\left(\begin{array}{l}-\frac{1}{2}{\left(80\text{mm}\right)}^2\left(50\text{rad}/\text{s}\right)\left(12\text{rad}/\text{s}\right)\\ +\left(120\text{mm}\right)\left(150\text{mm}\right)\left(8\text{rad}/{\text{s}}^2\right)\\ +\left(60\text{mm}\right)\left(150\text{mm}\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)\\ E_y=\frac{2.5\text{kg}}{2\left(150\text{mm}\right)}\left(\begin{array}{l}-\frac{1}{2}{\left(80\text{mm}\right)}^2\left(50\text{rad}/\text{s}\right)\left(12\text{rad}/\text{s}\right)\\ +\left(120\text{mm}\right)\left(150\text{mm}\right)\left(8\text{rad}/{\text{s}}^2\right)\\ +\left(60\text{mm}\right)\left(150\text{mm}\right){\left(12\text{rad}/\text{s}\right)}^2\end{array}\right)\\ E_y=-4\text{N}\end{array}$

Hence, dynamic reaction at $E$ is $\left(21\text{N}\right)i+\left(-4\text{N}\right)j$

Conclusion:

The dynamic reactions at $D$ is $\left(-21\text{N}\right)i+\left(28\text{N}\right)j$.

The dynamic reactions at $E$ is $\left(-21\text{N}\right)i+\left(-4\text{N}\right)j$.