Chapter 18.2, Problem 18.77P

To determine

(a)

The couple ${\text{M}}_0$.

Answer to Problem 18.77P

The couple ${\text{M}}_0$ is $247.48\times {10}^{-4}\text{N}\cdot \text{m}$.

Explanation of Solution

Given information:

The total mass is $600\text{g}$, the distance between the bearing is $150\text{mm}$ and the angular acceleration is $\left(12\text{rad}/{\text{s}}^{\text{2}}\right)k$.

Write the expression for the sum of the moment acting on the body along x -direction.

$\sum M_x=-I_{xz}\alpha +I_{yz}{\omega }^2$ ...... (I)

Here, the product of the moment of the inertia of $xz$ plane is $I_{xz}$, the product of the mass moment of the inertia of $yz$ plane is $I_{yz}$, angular velocity is $\omega$ and the angular acceleration is $\alpha$.

Write the expression for the sum of the moment acting on the body along y -direction.

$\sum M_y=-I_{yz}\alpha -I_{xz}{\omega }^2$ ...... (II)

Write the expression for the sum of the moment acting on the body along z -direction.

$\sum M_z=I_z\alpha$ ...... (III)

Here, the moment of the inertia along the z -direction is $I_z$.

Draw the diagram for the for the sheet metal component.

Figure-(1)

Write the expression for the area of the section 1 shown in the Figure-(1).

$A_1=\frac{1}{2}{b}^2$

Here, the constant dimension is $b$.

Write the expression for the area of the section 2 shown in the Figure-(1).

$A_2=\frac{1}{2}{b}^2$

Write the expression for the area of the section 3 shown in the Figure-(1).

$A_3=2b^2$ ...... (IV)

Write the expression for the total area of the sheet.

$A=A_1+A_2+A_3$ ...... (V)

Substitute $\frac{1}{2}{b}^2$ for $A_1$, $\frac{1}{2}{b}^2$ for $A_2$ and $2b^2$ for $A_3$ in Equation (IV).

$\begin{array}{c}A=\frac{1}{2}{b}^2+\frac{1}{2}{b}^2+2b^2\\ =b^2+2b^2\\ =3b^2\end{array}$ ...... (VI)

Write the expression of mass per unit area of the system.

$\rho =\frac{m}{A}$ ....... (VII)

Here, the mass of the sheet metal component is $m$.

Write the expression for the variation of the $y$ coordinate of section 1 in Figure-(1).

$y=\frac{b}{2}-z$ ….... (VIII)

Here, the coordinate of the considered point is $z$.

The below figure represent the schematic diagram of the elemental strip of section 1.

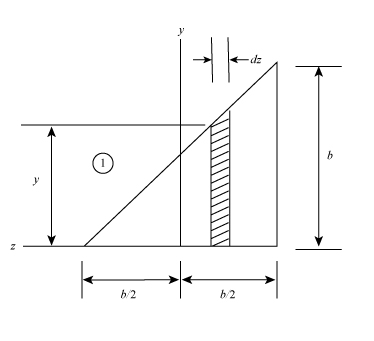
  Figure-(2)

Write the expression for the distance of the centroid of the element from the $z$ -axis in Figure-(2).

$\left(d_z\right)=\sqrt{b^2+\frac{y^2}{4}}$ ...... (IX)

Write the expression for the mass of the elemental strip.

$dm=\rho ydz$ ...... (X)

Here, the area of the elemental strip is $ydz$.

Write the expression for the moment of inertia of the element with respect to z- axis.

$d{I}_z=\rho \left(\frac{13}{24}{b}^3-\frac{1}{3}{z}^3+\frac{b}{2}{z}^2-\frac{5}{4}{b}^{2}z\right)dz$ ...... (XI)

Write the expression for the moment of the inertia of the section 1.

${\left(I_z\right)}_1=\frac{7}{12}\rho b^4$ ...... (XII)

Write the expression for the product of moment of inertia of the plane $xz$ for the section 1.

${\left(I_{xz}\right)}_1=\frac{1}{12}\rho b^4$ ...... (XIII)

Write the expression for the product of moment of inertia of the plane $yz$ for the section 1.

${\left(I_{yz}\right)}_1=-\frac{1}{24}\rho b^4$ ...... (XIV)

Write the expression for the variation of the $y$ coordinate of section 2 in Figure-(1).

$y=z-\frac{b}{2}$ ….... (XV)

The below figure represent the schematic diagram of the elemental strip of section 2.

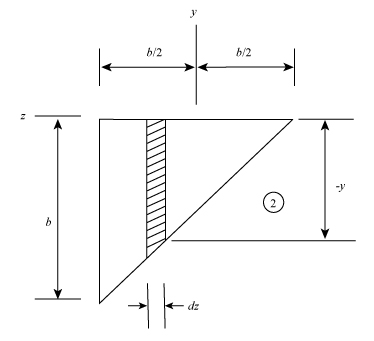
Figure-(3)

Write the expression for the mass of the elemental strip of section 2.

$dm=-\rho ydz$ ...... (XVI)

Write the expression for the moment of the inertia of the section 2.

${\left(I_z\right)}_2=\frac{7}{12}\rho b^4$ ...... (XVII)

Write the expression for the product of moment of inertia of the plane $xz$ for the section 2.

${\left(I_{xz}\right)}_2=\frac{1}{12}\rho b^4$ ...... (XVIII)

Write the expression for the product of moment of inertia of the plane $yz$ for the section 2.

${\left(I_{yz}\right)}_2=-\frac{1}{24}\rho b^4$ ...... (XIX)

Write the expression of mass per unit area of the section3 in Figure-(1).

$\rho =\frac{m_3}{A_3}$ ....... (XX)

Here, the mass of the rectangular sheet metal component is $m_3$.

Write the expression for the moment of the inertia of the section 3.

${\left(I_z\right)}_3=\frac{1}{12}{m}_3{\left(2b\right)}^2$ ...... (XXI)

The product moment of the inertia for the plane $yz$ and $xz$ of the section 3 of Figure-(1) is zero due to symmetry.

Write the expression for the moment of the inertia of the whole system.

$I_z={\left(I_z\right)}_1+{\left(I_z\right)}_2+{\left(I_z\right)}_3$ ...... (XXII)

Write the expression for the product of moment of inertia of the whole system.

$I_{xz}={\left(I_{xz}\right)}_1+{\left(I_{xz}\right)}_2+{\left(I_{xz}\right)}_3$ ...... (XXIII)

Write the expression for the product of moment of inertia of the whole system.

$I_{yz}={\left(I_{yz}\right)}_1+{\left(I_{yz}\right)}_2+{\left(I_{yz}\right)}_3$ ...... (XXIV)

Draw the diagram for the system to shows the action of forces on the system.

Figure-(4)

Here, the reaction on the point $A$ along the $x$ -direction is $A_x$, the reaction on the point $A$ along the $y$ -direction is $A_y$, the reaction on the point $B$ along the $x$ -direction is $B_x$ and the reaction on the point $B$ along the $y$ -direction is $B_y$.

Calculation:

Substitute $75\text{mm}$ for $b$ in Equation (VI).

$\begin{array}{c}A=3{\left(75\text{mm}\right)}^2\\ =3{\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^2\\ =1.687\times {10}^{-2}{\text{m}}^{\text{2}}\end{array}$

Substitute $1.687\times {10}^{-2}{\text{m}}^{\text{2}}$ for $A$ and $600\text{g}$ for $m$ in Equation (VII).

$\begin{array}{c}\rho =\frac{600\text{g}}{1.687\times {10}^{-2}{\text{m}}^{\text{2}}}\\ =\frac{600\text{g}\left(\frac{1\text{kg}}{1000\text{g}}\right)}{1.687\times {10}^{-2}{\text{m}}^{\text{2}}}\\ =\frac{0.6\text{kg}}{1.687\times {10}^{-2}{\text{m}}^{\text{2}}}\\ =35.55\text{kg}/{\text{m}}^{\text{2}}\end{array}$

Substitute $35.55\text{kg}/{\text{m}}^{\text{2}}$ for $\rho$ and $75\text{mm}$ for $b$ in Equation (XII).

$\begin{array}{c}{\left(I_z\right)}_1=\frac{7}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\right)}^4\\ =\frac{7}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^4\\ =\left(0.583\right)\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right)\left(3.164\times {10}^{-5}{\text{m}}^4\right)\\ =6.562\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $35.55\text{kg}/{\text{m}}^{\text{2}}$ for $\rho$ and $75\text{mm}$ for $b$ in Equation (XVII).

$\begin{array}{c}{\left(I_z\right)}_1=\frac{7}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\right)}^4\\ =\frac{7}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^4\\ =\left(0.583\right)\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right)\left(3.164\times {10}^{-5}{\text{m}}^4\right)\\ =6.562\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $75\text{mm}$ for $b$ in Equation (IV).

$\begin{array}{c}{A}_3=2{\left(75\text{mm}\right)}^2\\ =2{\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^2\\ =1.125\times {10}^{-2}{\text{m}}^{\text{2}}\end{array}$

Substitute $1.125\times {10}^{-2}{\text{m}}^{\text{2}}$ for $A_3$ and $35.55\text{kg}/{\text{m}}^{\text{2}}$ for $\rho$ in Equation (XX).

$\begin{array}{l}35.55\text{kg}/{\text{m}}^{\text{2}}=\frac{m_3}{1.125\times {10}^{-2}{\text{m}}^{\text{2}}}\\ m_3=\left(1.125\times {10}^{-2}{\text{m}}^{\text{2}}\right)\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right)\\ m_3=0.3339\text{kg}\\ m_3\approx 0.4\text{kg}\end{array}$

Substitute $0.4\text{kg}$ for $m_3$ and $75\text{mm}$ for $b$ in Equation (XXI).

$\begin{array}{c}{\left(I_z\right)}_3=\frac{1}{12}\left(\text{0}\text{.4}\text{kg}\right){\left(2\left(\text{75}\text{mm}\right)\right)}^2\\ =\frac{1}{12}\left(\text{0}\text{.4}\text{kg}\right){\left(2\left(\text{75}\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)\right)}^2\\ =\left(0.833\right)\left(\text{0}\text{.4}\text{kg}\right)\left(\text{0}\text{.0225}{\text{m}}^2\right)\\ =7.5\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $7.5\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for ${\left(I_z\right)}_3$, $6.562\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for ${\left(I_z\right)}_2$ and $6.562\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for ${\left(I_z\right)}_1$ in Equation

$\begin{array}{c}{I}_z=\left(6.562\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)+\left(6.562\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)+\left(7.5\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\\ =\left(6.562+6.562+7.5\right){10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\\ =20.624\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $20.624\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for $I_z$, $12\text{rad}/{\text{s}}^{\text{2}}$ for $\alpha$ and ${\text{M}}_0$ for $\sum M_z$ in Equation (III).

$\begin{array}{c}{\text{M}}_0=\left(20.624\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\left(12\text{rad}/{\text{s}}^{\text{2}}\right)\\ =247.48\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}/{\text{s}}^2\left(\frac{1\text{N}}{1\text{kg}\cdot \text{m}/{\text{s}}^{\text{2}}}\right)\\ =247.48\times {10}^{-4}\text{N}\cdot \text{m}\end{array}$

Conclusion:

The couple ${\text{M}}_0$ is $247.48\times {10}^{-4}\text{N}\cdot \text{m}$.

To determine

(b)

The dynamic reactions at $A$.

The dynamic reactions at $B$.

Answer to Problem 18.77P

The dynamic reactions at $A$ is $\left(74.96\times {10}^{-4}\text{N}\right)i+\left(149.92\times {10}^{-4}\text{N}\right)j$ .

The dynamic reactions at $B$ is $-\left(74.96\times {10}^{-4}\text{N}\right)i-\left(149.92\times {10}^{-4}\text{N}\right)j$ .

Explanation of Solution

Write the expression for the dynamic reaction at point $A$.

$A=A_{x}i+A_{y}j$ ...... (XXV)

Write the expression for the dynamic reaction at point $B$.

$B=B_{x}i+B_{y}j$ ...... (XXVI)

Write the expression for the reaction forces along the y- direction.

$A_y=-B_y$ ...... (XXVII)

Write the expression for the reaction forces along the x- direction.

$A_x=-B_x$ ...... (XXVIII)

Write the expression for the sum of the moment acting on the body along x -direction.

$\sum M_x=-c{A}_y$

Here, distance between the point $A$ and $B$ is $c$ .,

Write the expression for the sum of the moment acting on the body along y -direction.

$\sum M_y=c{A}_x$

Calculation:

Substitute $35.55\text{kg}/{\text{m}}^{\text{2}}$ for $\rho$ and $75\text{mm}$ for $b$ in Equation (XIII).

$\begin{array}{c}{\left(I_{xz}\right)}_1=\frac{1}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\right)}^4\\ =\frac{1}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^4\\ =\left(0.833\right)\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right)\left(3.164\times {10}^{-5}{\text{m}}^4\right)\\ =9.37\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $35.55\text{kg}/{\text{m}}^{\text{2}}$ for $\rho$ and $75\text{mm}$ for $b$ in Equation (XVIII).

$\begin{array}{c}{\left(I_{xz}\right)}_2=\frac{1}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\right)}^4\\ =\frac{1}{12}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^4\\ =\left(0.833\right)\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right)\left(3.164\times {10}^{-5}{\text{m}}^4\right)\\ =9.37\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $35.55\text{kg}/{\text{m}}^{\text{2}}$ for $\rho$ and $75\text{mm}$ for $b$ in Equation (XIV).

$\begin{array}{c}{\left(I_{yz}\right)}_1=-\frac{1}{24}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\right)}^4\\ =-\frac{1}{24}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^4\\ =-\left(0.0416\right)\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right)\left(3.164\times {10}^{-5}{\text{m}}^4\right)\\ =-4.68\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $35.55\text{kg}/{\text{m}}^{\text{2}}$ for $\rho$ and $75\text{mm}$ for $b$ in Equation (XIX).

$\begin{array}{c}{\left(I_{yz}\right)}_2=-\frac{1}{24}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\right)}^4\\ =-\frac{1}{24}\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right){\left(75\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)\right)}^4\\ =-\left(0.0416\right)\left(35.55\text{kg}/{\text{m}}^{\text{2}}\right)\left(3.164\times {10}^{-5}{\text{m}}^4\right)\\ =-4.68\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $9.37\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}$ for ${\left(I_{xz}\right)}_2$, $9.37\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}$ for ${\left(I_{xz}\right)}_1$ and $0$ for ${\left(I_{xz}\right)}_3$ in Equation (XXIII).

$\begin{array}{c}{I}_{xz}=\left(9.37\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\right)+\left(9.37\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\right)+0\\ =1.874\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $-4.68\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}$ for ${\left(I_{yz}\right)}_2$, $-4.68\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}$ for ${\left(I_{yz}\right)}_1$ and $0$ for ${\left(I_{yz}\right)}_3$ in Equation (XXIV).

$\begin{array}{c}{I}_{yz}=\left(-4.68\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\right)+\left(-4.68\times {10}^{-5}\text{kg}\cdot {\text{m}}^{\text{2}}\right)+0\\ =-0.937\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\end{array}$

Substitute $-c{A}_y$ for $\sum M_x$, $1.874\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for $I_{xz}$, $-0.937\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for $I_{yz}$, $12\text{rad}/{\text{s}}^{\text{2}}$ for $\alpha$ and $0$ for $\omega$ in Equation (I).

$\begin{array}{l}-c{A}_y=-\left(1.874\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\left(12\text{rad}/{\text{s}}^{\text{2}}\right)+\left(-0.937\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\left(0\right)\\ -c{A}_y=-\left(1.874\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\left(12\text{rad}/{\text{s}}^{\text{2}}\right)+0\\ A_y=\frac{22.48\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}/{\text{s}}^{\text{2}}}{c}\end{array}$ … (XXIX)

Substitute $150\text{mm}$ for $c$ in Equation (XXIX).

$\begin{array}{c}{A}_y=\frac{22.48\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}/{\text{s}}^{\text{2}}}{150\text{mm}}\\ =\frac{22.48\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}/{\text{s}}^{\text{2}}\left(\frac{1\text{N}}{1\text{kg}\cdot \text{m}/{\text{s}}^{\text{2}}}\right)}{150\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)}\\ =\frac{22.48\times {10}^{-4}\text{N}\cdot \text{m}}{0.150\text{m}}\\ =149.92\times {10}^{-4}\text{N}\end{array}$

Substitute $-c{A}_x$ for $\sum M_y$, $1.874\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for $I_{xz}$, $-0.937\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}$ for $I_{yz}$, $12\text{rad}/{\text{s}}^{\text{2}}$ for $\alpha$ and $0$ for $\omega$ in Equation (II).

$\begin{array}{l}c{A}_x=-\left(-0.937\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\left(12\text{rad}/{\text{s}}^{\text{2}}\right)-\left(1.874\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\left(0\right)\\ c{A}_x=\left(0.937\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}\right)\left(12\text{rad}/{\text{s}}^{\text{2}}\right)-0\\ A_x=\frac{11.24\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}/{\text{s}}^{\text{2}}}{c}\end{array}$ … (XXX)

Substitute $150\text{mm}$ for $c$ in Equation (XXX).

$\begin{array}{c}{A}_x=\frac{11.24\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}/{\text{s}}^{\text{2}}}{150\text{mm}}\\ =\frac{11.24\times {10}^{-4}\text{kg}\cdot {\text{m}}^{\text{2}}/{\text{s}}^{\text{2}}\left(\frac{1\text{N}}{1\text{kg}\cdot \text{m}/{\text{s}}^{\text{2}}}\right)}{150\text{mm}\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)}\\ =\frac{11.24\times {10}^{-4}\text{N}\cdot \text{m}}{0.150\text{m}}\\ =74.96\times {10}^{-4}\text{N}\end{array}$

Substitute $74.96\times {10}^{-4}\text{N}$ for $A_x$ and $149.92\times {10}^{-4}\text{N}$ for $A_y$ in Equation (XXV).

$A=\left(74.96\times {10}^{-4}\text{N}\right)i+\left(149.92\times {10}^{-4}\text{N}\right)j$

Substitute $149.92\times {10}^{-4}\text{N}$ for $A_y$ in Equation (XXVII).

$B_y=-149.92\times {10}^{-4}\text{N}$

Substitute $74.96\times {10}^{-4}\text{N}$ for $A_x$ in Equation (XXVIII).

$B_x=-74.96\times {10}^{-4}\text{N}$

Substitute $-74.96\times {10}^{-4}\text{N}$ for $B_x$ and $-149.92\times {10}^{-4}\text{N}$ for $B_y$ in Equation (XXVI).

$\begin{array}{c}B=\left(-74.96\times {10}^{-4}\text{N}\right)i+\left(-149.92\times {10}^{-4}\text{N}\right)j\\ =-\left(74.96\times {10}^{-4}\text{N}\right)i-\left(149.92\times {10}^{-4}\text{N}\right)j\end{array}$

Conclusion:

The dynamic reactions at $A$ is $\left(74.96\times {10}^{-4}\text{N}\right)i+\left(149.92\times {10}^{-4}\text{N}\right)j$ .

The dynamic reactions at $B$ is $-\left(74.96\times {10}^{-4}\text{N}\right)i-\left(149.92\times {10}^{-4}\text{N}\right)j$ .