Precalculus: Graphical, Numerical, Algebraic Common Core 10th Edition
10th Edition
ISBN: 9780134673301
Author: Waits, Foley, Kennedy, Bock Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Expert Solution & Answer
Chapter 1.7, Problem 51E
Solution
(a)
To find: The scatter graph of given data.
The graph is given
Given information:
| Time(min) | Temperature | Time (L2) | Temperature |
| 1 | 184.3 | 11 | 140 |
| 2 | 178.5 | 12 | 136.1 |
| 3 | 173.5 | 13 | 133.5 |
| 4 | 168.6 | 14 | 130.5 |
| 5 | 164.0 | 15 | 127.9 |
| 6 | 159.2 | 16 | 125 |
| 7 | 155.1 | 17 | 122.8 |
| 8 | 151.8 | 18 | 119.9 |
| 9 | 147 | 19 | 117.2 |
| 10 | 143.7 | 20 | 115.2 |
Graph of time from L1 and temperature from L2 is given below.
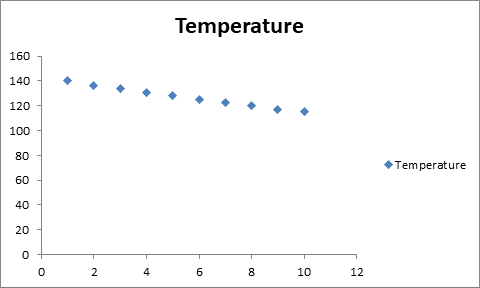
(b)
To find: Store L2-72 and find L3.
The table is given
Given information:
| L3 Time | temperature |
| 21 | 68 |
| 22 | 64.1 |
| 23 | 61.5 |
| 24 | 68.5 |
| 25 | 55.9 |
| 26 | 53 |
| 27 | 50.8 |
| 28 | 47.9 |
| 29 | 45.2 |
| 30 | 43.2 |
(c)
To find: Find the exponential regression for L3.
The exponential regression for L3 is y=73.71⋅(0.9485)x
Given information:
| L3 Time | temperature |
| 21 | 68 |
| 22 | 64.1 |
| 23 | 61.5 |
| 24 | 68.5 |
| 25 | 55.9 |
| 26 | 53 |
| 27 | 50.8 |
| 28 | 47.9 |
| 29 | 45.2 |
| 30 | 43.2 |
The curve to be fitted is y=abx taking logarithm on both sides, we get
log10(y)=log10(a)+xlog10(b)
y=a+bx where Y=log10(y), A=log10(a),B=log10(b)
which linear in Y,x
So the corresponding normal equations are
∑Y=nA+B∑x
∑xY=A∑x+B∑x2
The values are calculated using the following table
| x | y | Y=log10(y) | x2 | x·Y |
| 1 | 68 | 1.8325 | 1 | 1.8325 |
| 2 | 64.1 | 1.8069 | 4 | 3.6137 |
| 3 | 61.5 | 1.7889 | 9 | 5.3666 |
| 4 | 68.5 | 1.8357 | 16 | 7.3428 |
| 5 | 55.9 | 1.7474 | 25 | 8.7371 |
| 6 | 53 | 1.7243 | 36 | 10.3457 |
| 7 | 50.8 | 1.7059 | 49 | 11.941 |
| 8 | 47.9 | 1.6803 | 64 | 13.4427 |
| 9 | 45.2 | 1.6551 | 81 | 14.8962 |
| 10 | 43.2 | 1.6355 | 100 | 16.3548 |
| --- | --- | --- | --- | --- |
| ∑x=55 | ∑y=558.1 | ∑Y=17.4124 | ∑x2=385 | ∑x· Y=93.8731 |
Substituting these values in the normal equations
10A+55B=17.4124
55A+385B=93.8731
Use elimination method we obtain A=1.8676,B=-0.023
∴a=antilog10(A)=antilog10(1.8676)=73.7191 and b=antilog10(B)=antilog10(-0.023)=0.9485
Now substituting this values in the equation is y=abx , we get y=73.71⋅(0.9485)x
Chapter 1 Solutions
Precalculus: Graphical, Numerical, Algebraic Common Core 10th Edition
Ch. 1.1 - Prob. 1QRCh. 1.1 - Prob. 2QRCh. 1.1 - Prob. 3QRCh. 1.1 - Prob. 4QRCh. 1.1 - Prob. 5QRCh. 1.1 - Prob. 6QRCh. 1.1 - Prob. 7QRCh. 1.1 - Prob. 8QRCh. 1.1 - Prob. 9QRCh. 1.1 - Prob. 10QR
Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10ECh. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.2 - Prob. 1QRCh. 1.2 - Prob. 2QRCh. 1.2 - Prob. 3QRCh. 1.2 - Prob. 4QRCh. 1.2 - Prob. 5QRCh. 1.2 - Prob. 6QRCh. 1.2 - Prob. 7QRCh. 1.2 - Prob. 8QRCh. 1.2 - Prob. 9QRCh. 1.2 - Prob. 10QRCh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.3 - Prob. 1QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 4QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 6QRCh. 1.3 - Prob. 7QRCh. 1.3 - Prob. 8QRCh. 1.3 - Prob. 9QRCh. 1.3 - Prob. 10QRCh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - In Exercises 112, each graph is a slight variation...Ch. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.4 - Prob. 1QRCh. 1.4 - Prob. 2QRCh. 1.4 - Prob. 3QRCh. 1.4 - Prob. 4QRCh. 1.4 - Prob. 5QRCh. 1.4 - Prob. 6QRCh. 1.4 - Prob. 7QRCh. 1.4 - Prob. 8QRCh. 1.4 - Prob. 9QRCh. 1.4 - Prob. 10QRCh. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.5 - Prob. 1QRCh. 1.5 - Prob. 2QRCh. 1.5 - Prob. 3QRCh. 1.5 - Prob. 4QRCh. 1.5 - Prob. 5QRCh. 1.5 - Prob. 6QRCh. 1.5 - Prob. 7QRCh. 1.5 - Prob. 8QRCh. 1.5 - Prob. 9QRCh. 1.5 - Prob. 10QRCh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - In Exercises 1322, find a formula for f1x . Give...Ch. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.6 - Prob. 1QRCh. 1.6 - Prob. 2QRCh. 1.6 - Prob. 3QRCh. 1.6 - Prob. 4QRCh. 1.6 - Prob. 5QRCh. 1.6 - Prob. 6QRCh. 1.6 - Prob. 7QRCh. 1.6 - Prob. 8QRCh. 1.6 - Prob. 9QRCh. 1.6 - Prob. 10QRCh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.7 - Prob. 1QRCh. 1.7 - Prob. 2QRCh. 1.7 - Prob. 3QRCh. 1.7 - Prob. 4QRCh. 1.7 - Prob. 5QRCh. 1.7 - Prob. 6QRCh. 1.7 - Prob. 7QRCh. 1.7 - Prob. 8QRCh. 1.7 - Prob. 9QRCh. 1.7 - Prob. 10QRCh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - In Exercises 110, write a mathematical expression...Ch. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - In Exercises 1114, choose a variable and write a...Ch. 1.7 - Prob. 15ECh. 1.7 - In Exercises 1520, write the specified quantity as...Ch. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - In Exercises 2136, write an equation for the...Ch. 1.7 - Finding the Model and Solving Water is stored in a...Ch. 1.7 - Prob. 38ECh. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Prob. 46ECh. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Prob. 51ECh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - In Exercises 5964, write the specified quantity as...Ch. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 67RECh. 1 - Prob. 68RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- (3) (20 points) Let F(x, y, z) = (y, z, x²z). Define E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}. (a) (2 points) Calculate the divergence V. F. (b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that the triple integral √ (V · F) dV = √ 2²(1. = x²(1 − x² - y²) dA. Earrow_forward(2) (22 points) Let F(x, y, z) = (x sin y, cos y, ―xy). (a) (2 points) Calculate V. F. (b) (6 points) Given a vector field is everywhere defined with V G₁(x, y, z) = * G2(x, y, z) = − G3(x, y, z) = 0. 0 0 F(x, y, z) = (F₁(x, y, z), F₂(x, y, z), F(x, y, z)) that F = 0, let G = (G1, G2, G3) where F₂(x, y, y, t) dt - √ F³(x, t, 0) dt, * F1(x, y, t) dt, t) dt - √ F Calculate G for the vector field F(x, y, z) = (x sin y, cos y, -xy).arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √(x + y) A R R = {(x, y) | 25 < x² + y² ≤ 36, x < 0} Hint: The integral and Region is defined in rectangular coordinates.arrow_forward
- Find the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). R - 1 · {(r,0) | 1 ≤ r≤ 5,½π≤ 0<1π}. Hint: Be sure to convert to Polar coordinates. Use the correct differential for Polar Coordinates.arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √2(x+y) dA R R = {(x, y) | 4 < x² + y² < 25,0 < x} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardHW: The frame shown in the figure is pinned at A and C. Use moment distribution method, with and without modifications, to draw NFD, SFD, and BMD. B I I 40 kN/m A 3 m 4 marrow_forwardLet the region R be the area enclosed by the function f(x)= = 3x² and g(x) = 4x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in the region R, find the volume of the solid. You may use a calculator and round to the nearest thousandth. y 11 10 9 00 8 7 9 5 4 3 2 1 -1 -1 x 1 2arrow_forward
- Let the region R be the area enclosed by the function f(x) = ex — 1, the horizontal line y = -4 and the vertical lines x = 0 and x = 3. Find the volume of the solid generated when the region R is revolved about the line y = -4. You may use a calculator and round to the nearest thousandth. 20 15 10 5 y I I I | I + -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 -5 I -10 -15 I + I I T I I + -20 I + -25 I I I -30 I 3.5 4 xarrow_forwardplease show all the workarrow_forwardplease show all the workarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Introduction to experimental design and analysis of variance (ANOVA); Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=vSFo1MwLoxU;License: Standard YouTube License, CC-BY