Chapter 17, Problem 11E

A “half-sinusoidal” waveform is shown in Fig. 17.31, which is the output of a half-wave rectifier used to help convert a sinusoidal input to dc. Find the Fourier series representation and plot the signal and Fourier series representation for n = 10 terms.

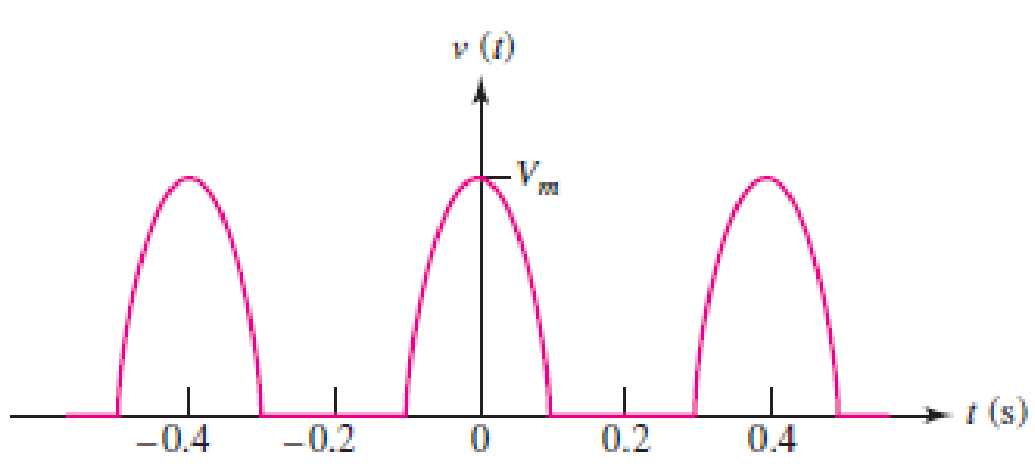
■ FIGURE 17.31

To determine

Find the Fourier series coefficients $a_0$, $a_n$, and $b_n$, and plot the signal and Fourier representation for $n=10$.

Answer to Problem 11E

The values of the Fourier series coefficients $a_0$, $a_n$, and $b_n$ is determined, and the signal $v\left(t\right)$ is sketched as shown in Figure 1.

Explanation of Solution

Given data:

Refer to Figure 17.31 in the textbook.

Formula used:

Write the general expression for Fourier series expansion.

$f\left(t\right)=a_0+{\displaystyle \sum _{n=1}^{\infty }\left(a_n\cos n{\omega }_{0}t+b_n\sin n{\omega }_{0}t\right)}$        (1)

Write the general expression for Fourier series coefficient $a_0$.

$a_0=\frac{1}{T}{\displaystyle {\int }_0^{T}f\left(t\right)}dt$        (2)

Write the general expression for Fourier series coefficient $a_n$.

$a_n=\frac{2}{T}{\displaystyle {\int }_0^{T}f\left(t\right)\cos n{\omega }_{0}t}dt$        (3)

Write the general expression for Fourier series coefficient $b_n$.

$b_n=\frac{2}{T}{\displaystyle {\int }_0^{T}f\left(t\right)\sin n{\omega }_{0}t}dt$        (4)

Write the expression to calculate the fundamental angular frequency.

${\omega }_0=\frac{2\pi }{T}=2\pi f_0$        (5)

Here,

$T$ is the period of the function.

Calculation:

In the given Figure 17.31, the time period is $T=0.4$.

The function $v\left(t\right)$ for the given waveform is,

$v\left(t\right)=\{\begin{array}{l}{V}_m\cos 5\pi t,-0.1\le t\le 0.1\\ 0,0.1\le t\le 0.3\end{array}$        (6)

Substitute 0.4 for T in equation (5) to find ${\omega }_0$.

${\omega }_0=\frac{2\pi }{0.4}$

${\omega }_0=5\pi$        (7)

Applying equation (6) in equation (2) to find $a_0$ as follows,

$\begin{array}{c}{a}_0=\frac{1}{0.4}{\displaystyle {\int }_0^{0.4}v\left(t\right)}dt\\ =\frac{1}{0.4}\left[{\displaystyle {\int }_{-0.1}^{0.1}{V}_m\cos 5\pi t}dt+{\displaystyle {\int }_{0.1}^{0.3}\left(0\right)}dt+\right]\\ =\frac{V_m}{0.4}{\left[\frac{\sin 5\pi t}{5\pi }\right]}_{-0.1}^{0.1}\\ =\frac{V_m}{0.4}\left[\frac{\sin 5\pi \left(0.1\right)}{5\pi }-\frac{\sin 5\pi \left(-0.1\right)}{5\pi }\right]\\ =\frac{V_m}{0.4}\left[\frac{1+1}{5\pi }\right]\end{array}$

Simplify the above equation as follows,

$a_0=\frac{V_m}{\pi }$

For half wave symmetry and even symmetry,

For all values of ‘n’, $b_n=0$.

Applying equation (6) in equation (3) to find the value of coefficient $a_n$.

$a_n=\frac{2}{0.4}{\displaystyle {\int }_0^{0.4}v\left(t\right)\cos n{\omega }_{0}t}dt$

$a_n=\frac{2V_m}{0.4}\left[{\displaystyle {\int }_{-0.1}^{0.1}\cos \left(5\pi t\right)\cos \left(5\pi nt\right)}dt\right]\left\{\because {\omega }_0=5\pi \right\}$        (8)

Consider the function,

$x={\displaystyle \int \cos \left(5\pi t\right)\cos \left(5\pi nt\right)dt}$

Consider,

$u=5\pi t$

On differentiating the above expression,

$\begin{array}{l}\frac{du}{dt}=5\pi \\ dt=\frac{du}{5\pi }\end{array}$

Equation (8) will be follows,

$x=\frac{1}{5\pi }{\displaystyle \int \cos \left(u\right)\cos \left(nu\right)du}$        (9)

In the above equation, consider,

$\begin{array}{c}y={\displaystyle \int \cos \left(u\right)\cos \left(nu\right)du}\\ ={\displaystyle \int \frac{\cos \left(nu+u\right)+\cos \left(nu-u\right)}{2}}du\left\{\because \cos \left(x\right)\cos \left(y\right)=\frac{1}{2}\left[\cos \left(y+x\right)+\cos \left(y-x\right)\right]\right\}\\ ={\displaystyle \int \frac{\cos \left(\left(n+1\right)u\right)+\cos \left(\left(n-1\right)u\right)}{2}}du\end{array}$

By applying linearity,

$y=\frac{1}{2}{\displaystyle \int \cos \left(\left(n+1\right)u\right)du}+\frac{1}{2}{\displaystyle \int \cos \left(\left(n-1\right)u\right)}du$        (10)

In equation (10),

consider,

$m={\displaystyle \int \cos \left(\left(n+1\right)u\right)du}$        (11)

Let,

$\begin{array}{l}v=\left(n+1\right)u\\ \frac{dv}{du}=\left(n+1\right)\\ du=\frac{dv}{n+1}\end{array}$

Equation (11) will be as follows,

$\begin{array}{c}m=\frac{1}{n+1}{\displaystyle \int \cos \left(v\right)dv}\\ =\frac{\sin \left(v\right)}{n+1}\\ =\frac{\sin \left(\left(n+1\right)u\right)}{n+1}\left\{\because v=\left(n+1\right)u\right\}\end{array}$

Similarly, in equation (10),

consider,

$l={\displaystyle \int \cos \left(\left(n-1\right)u\right)du}$        (12)

Let,

$\begin{array}{l}v=\left(n-1\right)u\\ \frac{dv}{du}=\left(n-1\right)\\ du=\frac{dv}{n-1}\end{array}$

Equation (12) will be as follows,

$\begin{array}{c}l=\frac{1}{n-1}{\displaystyle \int \cos \left(v\right)dv}\\ =\frac{\sin \left(v\right)}{n-1}\\ =\frac{\sin \left(\left(n-1\right)u\right)}{n-1}v=\left(n-1\right)u\end{array}$

Substitute the values of m and l in equation (10) as follows,

$\begin{array}{c}y=\frac{1}{2}\left[\frac{\sin \left(\left(n+1\right)u\right)}{n+1}+\frac{\sin \left(\left(n-1\right)u\right)}{n-1}\right]\\ =\frac{\sin \left(\left(n+1\right)u\right)}{2\left(n+1\right)}+\frac{\sin \left(\left(n-1\right)u\right)}{2\left(n-1\right)}\end{array}$

Substitute the value of y in equation (9) as follows,

$\begin{array}{c}x=\frac{1}{5\pi }\left[\frac{\sin \left(\left(n+1\right)u\right)}{2\left(n+1\right)}+\frac{\sin \left(\left(n-1\right)u\right)}{2\left(n-1\right)}\right]\\ =\frac{\sin \left(\left(n+1\right)u\right)}{10\pi \left(n+1\right)}+\frac{\sin \left(\left(n-1\right)u\right)}{10\pi \left(n-1\right)}\\ =\frac{\sin \left(5\pi \left(n+1\right)t\right)}{10\pi \left(n+1\right)}+\frac{\sin \left(5\pi \left(n-1\right)t\right)}{10\pi \left(n-1\right)}\left\{\because u=5\pi t\right\}\end{array}$

Therefore,

$\begin{array}{c}{\displaystyle \int \cos \left(5\pi t\right)\cos \left(5\pi nt\right)dt}=\frac{\sin \left(5\pi \left(n+1\right)t\right)}{10\pi \left(n+1\right)}+\frac{\sin \left(5\pi \left(n-1\right)t\right)}{10\pi \left(n-1\right)}\\ =\frac{\left(n-1\right)\sin \left(5\pi \left(n+1\right)t\right)+\left(n+1\right)\sin \left(5\pi \left(n-1\right)t\right)}{10\pi \left(n^2-1\right)}\end{array}$

On applying the limits,

$\begin{array}{c}{\displaystyle {\int }_{-0.1}^{0.1}\cos \left(5\pi t\right)\cos \left(5\pi nt\right)}dt={\left[\frac{\left(n-1\right)\sin \left(5\pi \left(n+1\right)t\right)+\left(n+1\right)\sin \left(5\pi \left(n-1\right)t\right)}{10\pi \left(n^2-1\right)}\right]}_{-0.1}^{0.1}\\ =\left[\frac{\left(n-1\right)\sin \left(5\pi \left(n+1\right)\left(0.1\right)\right)+\left(n+1\right)\sin \left(5\pi \left(n-1\right)\left(0.1\right)\right)}{10\pi \left(n^2-1\right)}\right]\\ -\left[\frac{\left(n-1\right)\sin \left(5\pi \left(n+1\right)\left(-0.1\right)\right)+\left(n+1\right)\sin \left(5\pi \left(n-1\right)\left(-0.1\right)\right)}{10\pi \left(n^2-1\right)}\right]\\ =\left[\frac{\left(n-1\right)\sin \left(\frac{n\pi +\pi }{2}\right)+\left(n+1\right)\sin \left(\frac{n\pi -\pi }{2}\right)}{10\pi \left(n^2-1\right)}\right]\\ -\left[\frac{-\left(n-1\right)\sin \left(\frac{n\pi +\pi }{2}\right)-\left(n+1\right)\sin \left(\frac{n\pi -\pi }{2}\right)}{10\pi \left(n^2-1\right)}\right]\\ =\left[\frac{\left(n-1\right)\sin \left(\frac{n\pi +\pi }{2}\right)+\left(n+1\right)\sin \left(\frac{n\pi -\pi }{2}\right)}{10\pi \left(n^2-1\right)}\right]+\\ \left[\frac{\left(n-1\right)\sin \left(\frac{n\pi +\pi }{2}\right)+\left(n+1\right)\sin \left(\frac{n\pi -\pi }{2}\right)}{10\pi \left(n^2-1\right)}\right]\end{array}$

Simplify the equation as follows,

$\begin{array}{c}{\displaystyle {\int }_{-0.1}^{0.1}\cos \left(5\pi t\right)\cos \left(5\pi nt\right)}dt=\frac{2\left[\left(n-1\right)\sin \left(\frac{n\pi +\pi }{2}\right)+\left(n+1\right)\sin \left(\frac{n\pi -\pi }{2}\right)\right]}{10\pi \left(n^2-1\right)}\\ =\frac{2\left[\left(n-1\right)\sin \left(\frac{n\pi }{2}+\frac{\pi }{2}\right)+\left(n+1\right)\sin \left(\frac{n\pi }{2}-\frac{\pi }{2}\right)\right]}{10\pi \left(n^2-1\right)}\\ =\frac{2\left[\left(n-1\right)\cos \left(\frac{n\pi }{2}\right)-\left(n+1\right)\cos \left(-\frac{n\pi }{2}\right)\right]}{10\pi \left(n^2-1\right)}\left\{\begin{array}{l}\because \sin \left(90+\theta \right)=\cos \theta ,\\ \sin \left(-\theta \right)=-\sin \theta \end{array}\right\}\\ =\frac{2\left[n\cos \left(\frac{n\pi }{2}\right)-\cos \left(\frac{n\pi }{2}\right)-\left(n+1\right)\cos \left(-\frac{n\pi }{2}\right)\right]}{10\pi \left(n^2-1\right)}\end{array}$

Simplify the equation as follows,

$\begin{array}{c}{\displaystyle {\int }_{-0.1}^{0.1}\cos \left(5\pi t\right)\cos \left(5\pi nt\right)}dt=\frac{2\left[n\cos \left(\frac{n\pi }{2}\right)-\cos \left(\frac{n\pi }{2}\right)-\left(n+1\right)\cos \left(\frac{n\pi }{2}\right)\right]}{10\pi \left(n^2-1\right)}\left\{\because \cos \left(-\theta \right)=\cos \theta \right\}\\ =\frac{2\left[n\cos \left(\frac{n\pi }{2}\right)-\cos \left(\frac{n\pi }{2}\right)-n\cos \left(\frac{n\pi }{2}\right)-\cos \left(\frac{n\pi }{2}\right)\right]}{10\pi \left(n^2-1\right)}\\ =\frac{2\left[-2\cos \left(\frac{n\pi }{2}\right)\right]}{10\pi \left(n^2-1\right)}\\ =\frac{-2\cos \left(\frac{n\pi }{2}\right)}{5\pi \left(n^2-1\right)}\end{array}$

Substitute the value of ${\displaystyle {\int }_{-0.1}^{0.1}\cos \left(5\pi t\right)\cos \left(5\pi nt\right)}dt$ in equation (8) as follows,

$\begin{array}{c}{a}_n=\frac{2V_m}{0.4}\left[\frac{-2\cos \left(\frac{n\pi }{2}\right)}{5\pi \left(n^2-1\right)}\right]\\ =\frac{-2V_m\cos \left(\frac{n\pi }{2}\right)}{\pi \left(n^2-1\right)}\end{array}$

$a_n=\frac{2V_m}{\pi }\frac{\cos \left(\frac{n\pi }{2}\right)}{\left(1-n^2\right)}\left(n\ne 1\right)$

Substitute the value of $a_0$, $a_n$, and $b_n$ in equation (1) as follows,

$\begin{array}{c}v\left(t\right)=\frac{V_m}{\pi }+{\displaystyle \sum _{n=1}^{\infty }\left(\left(\frac{2V_m}{\pi }\right)\left(\frac{\cos \left(\frac{n\pi }{2}\right)}{1-n^2}\right)\cos n{\omega }_{0}t+0\right)}\\ =\frac{V_m}{\pi }+{\displaystyle \sum _{n=1}^{\infty }\left(\left(\frac{2V_m}{\pi }\right)\left(\frac{\cos \left(\frac{n\pi }{2}\right)}{1-n^2}\right)\cos 5n\pi t\right)}\end{array}$

Representing through $n=10$,

$\begin{array}{c}v(t)=\frac{V_m}{\pi }+\frac{V_m}{2}\cos 5\pi t+\frac{2V_m}{3\pi }\cos 10\pi t-\frac{2V_m}{15\pi }\cos 20\pi t+\frac{2V_m}{35\pi }\cos 30\pi t\\ -\frac{2V_m}{63\pi }\cos 40\pi t+\frac{2V_m}{99\pi }\cos 50\pi t\end{array}$

By considering $V_m=1\text{V}$, the above equation will be as follows,

$\begin{array}{c}v(t)=\frac{1}{\pi }+\frac{1}{2}\cos 5\pi t+\frac{2}{3\pi }\cos 10\pi t-\frac{2}{15\pi }\cos 20\pi t+\frac{2}{35\pi }\cos 30\pi t\\ -\frac{2}{63\pi }\cos 40\pi t+\frac{2}{99\pi }\cos 50\pi t\end{array}$

Matlab code for the signal $v(t)$ is shown below:

t=linspace(-0.6,0.6,1000); % vector for time over 1000 points.

Vm=1;

v0=Vm/(pi); % constant.

for i=1:1000;

sum=0; 

     sum=sum+ 0.5*cos(5*pi*t(i)) + (2/(3*pi))*cos(10*pi*t(i)) - (2/(15*pi))*cos(20*pi*t(i)) + (2/(35*pi))*cos(30*pi*t(i)) - (2/(63*pi))*cos(40*pi*t(i)) + (2/(99*pi))*cos(50*pi*t(i));

vt(i)=v0+sum;

end

plot(t,vt)

xlabel('Time t in seconds')

ylabel('Voltage value')

title('Fourier representation of voltage signal v(t)')

Matlab output:

The Fourier representation of voltage signal $v\left(t\right)$ is shown in Figure 1.

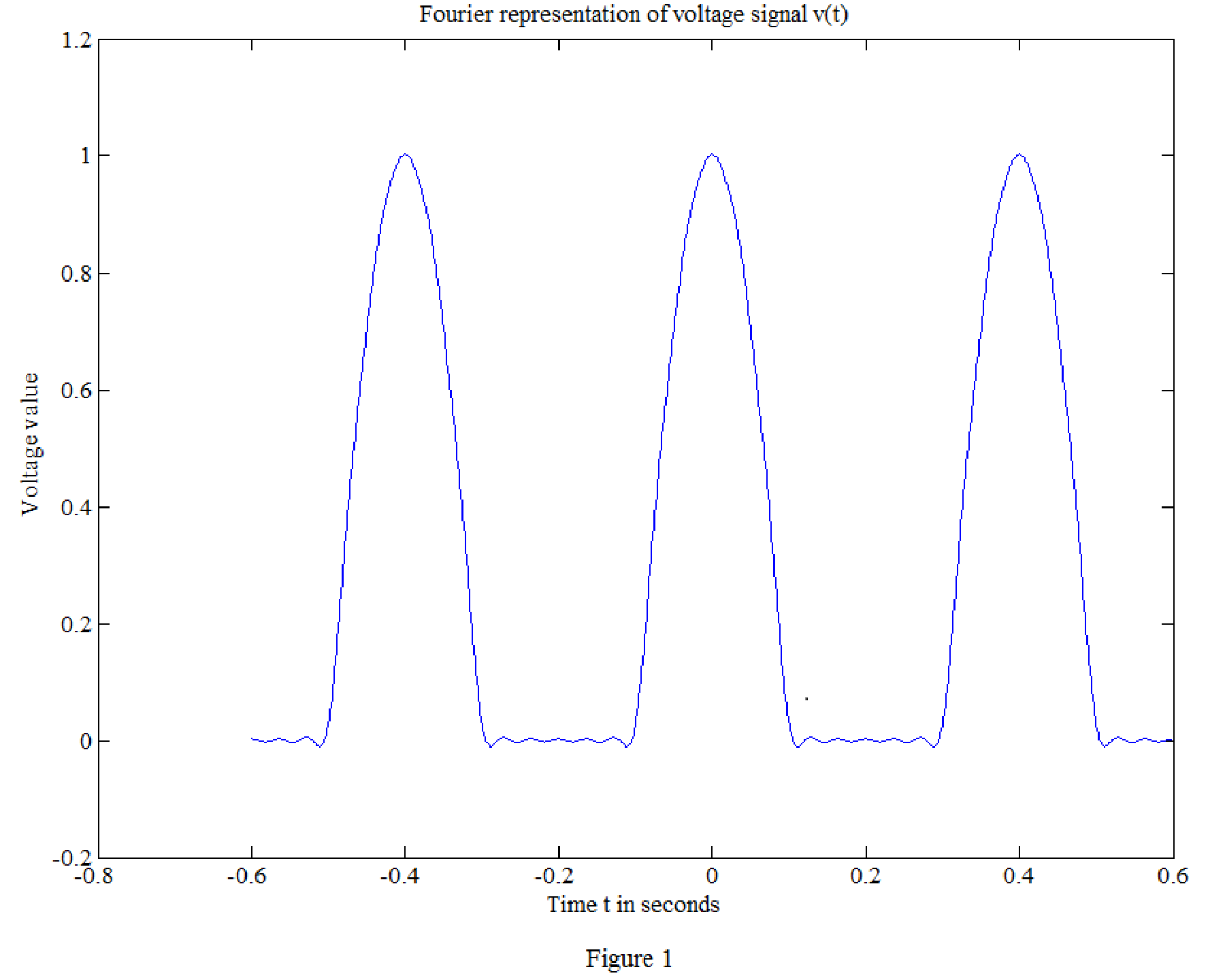
Conclusion:

Thus, the values of the Fourier series coefficients $a_0$, $a_n$, and $b_n$ is determined, and the signal $v\left(t\right)$ is sketched as shown in Figure 1.