Chapter 16.2, Problem 16.141P

Two rotating rods in the vertical plane are connected by a slider block P of negligible mass. The rod attached at A has a weight of 1.6 1b and a length of 8 in. Rod BP weighs 2 lb and is 10 in. long and the friction between block P and AE is negligible. The motion of the system is controlled by a couple M applied to rod BP. Knowing that rod BP has a constant angular velocity of 20 rad/s clockwise, determine (a) the couple M, (b) the components of the force exerted on AE by block P.

To determine

(a)

Find a couple of M.

Answer to Problem 16.141P

The couple of M=5.82Ib.in

Explanation of Solution

Given information:

The attached rod A weight is=1.6Lb

And length is=8in.

Rod BP weighs=2Lb

Length is=10in.

Explanation:

First consider the unit vector along the axis of X and Y direction.

So, we have to find the vertical distance from point P and point A(y).

$\begin{array}{l}y=\left[\left(10\right)\frac{1}{12}\right]\sin {30}^0\\ =0.4166ft\end{array}$

Determine the horizontal distance from point A to B(X)

$\begin{array}{l}x=\left[\left(10\right)\frac{1}{12}\right]\cos {30}^0\\ =0.7216ft\end{array}$

Here we take the coordinate points as (0,-0.4166ft)

Then the position of the vector $r_{P/A}=-\left(0.4166ft\right)j$

Coordinate points of the point P with the point B is (-0.7216ft,-0.4166ft)

Then the position vector is $r_{P/B}=-\left(0.7216ft\right)i-\left(0.4166ft\right)j$

Then the coordinate points with the point P and point E as (0,-8/12ft)

Position vector is $r_{P/E}=-\left(0.6666ft\right)j$

Here, the unit vector k as angular direction in clock wise as negative and it is positive when counter clockwise.

Angular velocity of the rod BP in vector form is,

$-\left(20rad/s\right)k$

Velocity of the rod BP is,

$\begin{array}{l}{v}_p={\omega }_{BP}{r}_{P/B}\\ v_p=\left[-\left(20rad/s\right)k\right]\left[-\left(0.7216ft\right)i-\left(0.4166ft\right)j\right]\\ =\left(14.432ft/s\right)\left(k\times i\right)+\left(8.3333ft/s\right)\left(k\times j\right)\\ =\left(14.432ft/s\right)j+\left(8.3333ft/s\right)\left(-i\right)\\ =\left(14.432ft/s\right)j-\left(8.3333ft/s\right)i----(1)\end{array}$

Formulate the velocity equation of point P

$\begin{array}{l}{v}_p=\left({\omega }_{AE}k\right)\left[-\left(0.4166ft\right)j\right]+uj\\ =-\left(0.4166{\omega }_{AE}\right)\left(k\times j\right)+uj\\ =-\left(0.4166{\omega }_{AE}\right)\left(-i\right)+uj\\ =\left(0.4166{\omega }_{AE}\right)i+uj---(2)\end{array}$

Compare the I terms from equation (1) And (2)

$\begin{array}{l}{\omega }_{AE}=-\frac{8.3333ft/s}{0.4166}\\ =-20rad/s\end{array}$

Compare the equation (1) and (2) for j terms

$u=\left(14.432ft/s\right)$

So, the angular acceleration is zero.

Formulate the acceleration of the rod BP

$\begin{array}{l}{a}_p=\left[\left({\alpha }_{BP}\right)\left(r_{P/B}\right)\right]-{\omega }_{BP}^2{r}_{P/B}\\ a_p=\left\{\left(0\right)\times \left(-0.7216ft\right)i-\left(0.4166ft\right)j-{\left(-\left(20rad/s\right)k\right)}^2\left(-\left(0.7216ft\right)i-\left(0.4166ft\right)j\right)\right\}\\ =0-\left(400\right)\left(-\left(0.7216ft\right)i-\left(0.4166ft\right)j\right)\\ =\left(288.68ft/s^2\right)i+\left(166.67ft/s^2\right)j---\left(3\right)\end{array}$

Find the acceleration of the point P to the point E

$\begin{array}{l}{a}_{p^1}=\left[\left({\alpha }_{AE}\right)\left(r_{P/A}\right)\right]-{\omega }_{AE}^2{r}_{P/A}\\ a_{p^{\text{'}}}=\left\{\left({\alpha }_{AE}k\right)\times \left(-0.4166ft\right)j-\left(0.4166ft\right)j-{\left(-\left(20rad/s\right)k\right)}^2\left[-\left(0.4166ft\right)j\right]\right\}\\ =-\left(0.4166{\alpha }_{AE}\right)\left(k\times j\right)-\left(400\right)\left[-\left(0.4166ft\right)j\right]\\ =-\left(0.4166{\alpha }_{AE}\right)\left(-i\right)+\left(166.67ft/s^2\right)j\\ =0.4166{\alpha }_{AE}i+\left(166.67ft/s^2\right)j\end{array}$

Formulate the acceleration at the point P

$a_p=a_{p^{\text{'}}}+a_{p/AE}+2{\omega }_{BP}\times v_{p/AE}$

Substitute the above values

$\begin{array}{l}{a}_P=0.4166{\alpha }_{AE}i+\left(166.67\right)j+0+2\left[-\left(20rad/s\right)k\right]\left(14.1338j\right)\\ =0.4166{\alpha }_{AE}i+\left(166.67\right)j-\left(577.352\right)\left(k\times j\right)\\ =0.4166{\alpha }_{AE}i+\left(166.67\right)j-\left(577.352\right)\left(-i\right)\\ =0.4166{\alpha }_{AE}i+\left(166.67\right)j+\left(277.352\right)i----(4)\end{array}$

Based on equations (3) and (4), we get,

$\begin{array}{l}\left(288.68\right)=0.4164{\alpha }_{AE}+\left(577.352\right)\\ 0.4164{\alpha }_{AE}=-288.672\\ {\alpha }_{AE}=-692.8rad/s^2\end{array}$

Find the mass of the rod AE

$\begin{array}{l}{m}_{AE}=\frac{W_{AE}}{g}\\ m_{AE}=\frac{1.6}{32.2}\\ =0.0496Ib.s^2/ft\end{array}$

Then the moment of inertial of the rod AE is

$\begin{array}{l}{I}_{AE}=\frac{m_{AE}{I}_{AE}^2}{12}\\ I_{AE}=\frac{0.0496\times 8in.\frac{1ft}{12in.}}{12}\\ =1.8403\times {10}^{-3}Ib.s^2.ft\end{array}$

Similarly find the mass of the rod BP

$\begin{array}{l}{m}_{BP}=\frac{W_{BP}}{g}\\ m_{BP}=\frac{2Ib}{32.2ft/s^2}\\ =0.0621Ib.s^2/ft\end{array}$

Then the moment of inertial of the rod BP is,

$\begin{array}{l}{I}_{BP}=\frac{m_{BP}{I}_{BP}^2}{12}\\ I_{BP}=\frac{0.0621\times 10in.\frac{1ft}{12in.}}{12}\\ =3.5944\times {10}^{-3}Ib.s^2.ft\end{array}$

Here, the mass of the centers of rod AE and BP are to be considered as G and H

Then the reference for point G with point A as (0,-4/12ft).

Here, the position vector is −(0.3333ft)j.

Similarly, the point H with point B as the reference as (-0.7216ft,-0.4166ft) position vector is −(0.7216ft)i-(0.4166ft)j.

Acceleration of the point G is get by

$a_G={\alpha }_{AE}{r}_{G/A}-{\omega }_{AE}^2{r}_{G/A}$

$\begin{array}{l}{a}_G=\left[\left(-692.8rad/s^2\right)k\right]\left[-\left(0.3333ft\right)j\right]-{\left[\left(-20rad/s\right)k\right]}^2\left[-\left(0.3333ft\right)j\right]\\ =\left(230.93ft/s^2\right)\left(k\times j\right)+\left(133.32ft/s^2\right)j\\ =\left(230.93ft/s^2\right)\left(-i\right)+\left(133.32ft/s^2\right)j\\ =-\left(230.93ft/s^2\right)\left(i\right)+\left(133.32ft/s^2\right)j\end{array}$

Find the acceleration at point H

$\begin{array}{l}{a}_H={\alpha }_{BP}{r}_{H/B}-{\omega }_{BP}^2{r}_{H/B}\\ a_H=\left\{(0)\left[-\left(0.7216\right)i-\left(0.4166\right)j\right]-{\left[\left(-20rad/s\right)k\right]}^2\left[-\left(0.7216\right)i-\left(0.4166\right)j\right]\right\}\\ =0+\left(288.64ft/s^2\right)i+\left(166.64ft/s^2\right)j\\ =\left(288.64ft/s^2\right)i+\left(166.64ft/s^2\right)j\end{array}$

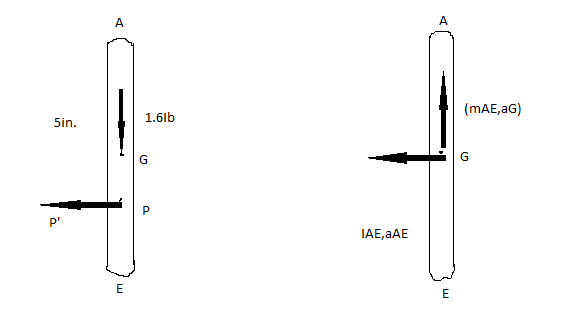
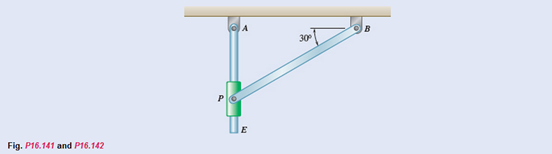
Considering the above diagram take the moment about point A

$\begin{array}{l}{r}_{P/A}\times \left(-\overline{P}i\right)=I_{AE}{\alpha }_{AE}+r_{G/A}\times \left(m_{AE}{a}_G\right)\\ -\left(\frac{5}{12}\right)j\times \left(-\overline{P}i\right)=\left\{\left(1.8403\times {10}^{-3}\right)\left(\left(-692.8\right)k\right)+\left(-\left(\frac{4}{12}\right)j\right)\times \left(0.0496\right)\left[-\left(230.93\right)i+\left(133.32\right)j\right]\right\}\\ (0.4166\overline{P})(j\times i)=-1.2750k+(3.8249)(j\times i)-(2.2042)(j\times i)\\ 0.4166\overline{P}k=-1.2750k-3.8249k-(2.2042)(0)\\ 0.4166\overline{P}k=-1.2750k-3.8249k\\ 0.4166\overline{P}=1.2750+3.8249\\ \overline{P}=12.240Ib\end{array}$

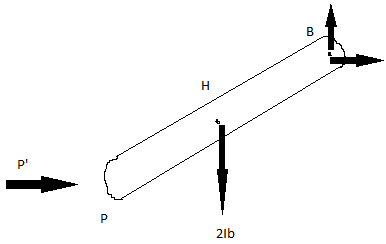
Based on above figure consider the moment about point B

$\left\{\left(-\left(\frac{5}{12}\right)j\right)\times \overline{P}i+\left(-\left(0.3608\right)i-\left(0.2083\right)j\right)\times \left(-2j\right)+Mk\right\}=\left\{\left(-\left(0.3608\right)i-\left(0.2083\right)j\right)\times \left[\left(0.0621\right)\left(\left(288.6\right)i+\left(166.64\right)j\right)+\left(3.5944\times {10}^{-3}\right)\left(0\right)\right]\right\}$

$\begin{array}{l}\left[-0.4166\overline{P}\left(j\times i\right)+\left(0.7216\right)\left(i\times j\right)+Mk\right]=\left\{\left(-\left(0.3608\right)i-\left(0.2083\right)j\right)\times \left[\left(\left(17.930\right)i+\left(10.352\right)j\right)+0\right]\right\}\\ \left\{0.4166\overline{P}k+\left(0.7216\right)k+Mk\right\}=-3.7354k+3.735k---(5)\end{array}$

Substitute the values

$\begin{array}{l}\left\{0.4166\overline{P}k+\left(0.7216\right)k+Mk\right\}=-3.7354k+3.735k\\ 5.1+0.7216+M=0\\ M=-5.82Ib.ft\end{array}$

The magnitude of the couple applied on the rod is BP. It is considered as 5.82Ib.ft acts in a clockwise direction.

To determine

(b)

Find the force exerted on rod AE.

Answer to Problem 16.141P

The force exerted by rod AE is F=12.240Ib

Explanation of Solution

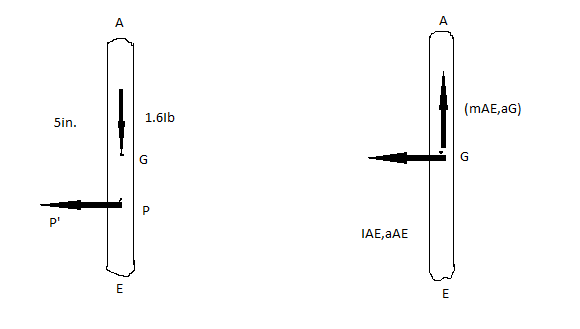
Considering the above diagram take the moment about point A

$\begin{array}{l}{r}_{P/A}\times \left(-\overline{P}i\right)=I_{AE}{\alpha }_{AE}+r_{G/A}\times \left(m_{AE}{a}_G\right)\\ -\left(\frac{5}{12}\right)j\times \left(-\overline{P}i\right)=\left\{\left(1.8403\times {10}^{-3}\right)\left(\left(-692.8\right)k\right)+\left(-\left(\frac{4}{12}\right)j\right)\times \left(0.0496\right)\left[-\left(230.93\right)i+\left(133.32\right)j\right]\right\}\\ (0.4166\overline{P})(j\times i)=-1.2750k+(3.8249)(j\times i)-(2.2042)(j\times i)\\ 0.4166\overline{P}k=-1.2750k-3.8249k-(2.2042)(0)\\ 0.4166\overline{P}k=-1.2750k-3.8249k\\ 0.4166\overline{P}=1.2750+3.8249\\ \overline{P}=12.240Ib\end{array}$

The force exerted by rod AE by block P is 12.240Ib. It is acted upon the left direction.