
Concept explainers
Solve Prob. 16.35, assuming that the couple M is applied to disk A.
i.
The angular acceleration of gear A.
Answer to Problem 16.36P
Angular acceleration of gear A = 6.057 rad/s2
Explanation of Solution
Given:
Mass of Gear A,ma = 9 kg
radius of gyration of gear A,
Mass of gear B, mb = 9 kg
radius of gyration of gear B,
Mass of Gear C,mc = 3 kg
radius of gyration of gear C,
Magnitude of Couple applied on gear A, M = 5N-m
Concept used:
Mass moment of acceleration is given by-
The tangential force acting on a gear will provide the angular acceleration to the gear. Therefore,
The free body diagram of the three gears is as following-
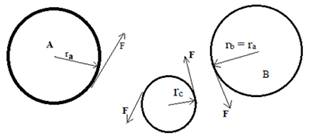
Calculation:
The tangential component of two gears in mesh will be equal, therefore,
Since,
For gear B,
Since, gear a A and B are of same size, therefore because of symmetry, gear C will exert same force on gear B as on gear A.
For gear C,
For gear A,
Angular acceleration of gear A,
Conclusion:
Angular acceleration of gear A = 6.057 rad/s2
ii.
The tangential force that gear A exerts on gear C.
Answer to Problem 16.36P
Force exerted by gear C on gear A = 11.278 N
Explanation of Solution
Given:
Mass of Gear A,ma = 9 kg
radius of gyration of gear A,
mass of gear B, mb = 9 kg
radius of gyration of gear B,
mass of Gear C,mc = 3 kg
radius of gyration of gear C,
Magnitude of Couple applied on gear A, M = 5N-m
Concept used:
Mass moment of acceleration is given by-
The tangential force acting on a gear will provide the angular acceleration to the gear. Therefore,
The free body diagram of the three gears is as following-

Calculation:
Angular acceleration of gear A = 6.057 rad/s2
The tangential component of two gears in mesh will be equal, therefore,
Since,
For gear B,
Since gear a A and B are of same size, therefore because of symmetry, gear C will exert same force on gear B as on gear A.
For gear C,
Angular acceleration of gear A,
Tangential force on gear A, on gearC-
Conclusion:
Force exerted by gear C on gear A = 11.278 N
Want to see more full solutions like this?
Chapter 16 Solutions
VECTOR MECH...,DYNAMICS(LOOSE)-W/ACCESS
- Please sovle this for me and please don't use aiarrow_forwardPlease sovle this for me and please don't use aiarrow_forward3. The cold-drawn AISI 1040 steel bar shown in the figure is subjected to a completely reversed axial load fluctuating between 28 kN in compression to 28 kN in tension. Estimate the fatigue factor of safety based on achieving infinite life (using Goodman line) and the yielding factor of safety. If infinite life is not predicted, estimate the number of cycles to failure. 25 mm + 6-mm D. 10 mmarrow_forward
- CORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE 1. The truss shown is supported by hinge at A and cable at E.Given: H = 4m, S = 1.5 m, α = 75⁰, θ = 33⁰.Allowable tensile stress in cable = 64 MPa.Allowable compressive stress in all members = 120 MPaAllowable tensile stress in all members = 180 MPa1.Calculate the maximum permissible P, in kN, if the diameter of the cable is 20 mm.2.If P = 40 kN, calculate the required area (mm2) of member BC.3. If members have solid square section, with dimension 15 mm, calculate the maximum permissible P (kN) based on the allowable strength of member HI.ANSWERS: (1) 45.6 kN; (2) 83.71 mm2; (3) 171.76 kNarrow_forwardCORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE 2: A wire 4 meters long is stretched horizontally between points 4 meters apart. The wire is 25 mm2 in cross-section with a modulus of elasticity of 200 GPa. A load W placed at the center of the wire produces a sag Δ.1.Calculate the tension (N) in the wire if sag Δ = 30 mm.2.Calculate the magnitude of W, in N, if sag Δ = 54.3 mm.3. If W is 60 N, what is the sag (in mm)?ANSWERS: (1) 562 N, (2) 100 N, (3) 45.8 Narrow_forwardCORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE 4 : A cable and pulley system at D is used to bring a 230-kg pole (ACB) to a vertical position as shown. The cable has tensile force T and is attached at C. The length of the pole is 6.0 m, the outer diameter is d = 140 mm, and the wall thickness t = 12 mm. The pole pivots about a pin at A. The allowable shear stress in the pin is 60 MPa and the allowable bearing stress is 90 MPa. The diameter of the cable is 8 mm.1.Find the minimum diameter (mm) of the pin at A to support the weight of the pole in the position shown.2.Calculate the elongation (mm) of the cable CD.3.Calculate the vertical displacement of point C, in mm.ANSWERS: (1) 6 mm, (2) 1.186 mm, (3) 1.337 mm--arrow_forward
- 1. Derive an expression for H(w) filter or bandpass/reject filter. = for the circuit below. Qualitatively determine if it's a high/lowpass L ell R ww Voarrow_forward2. Obtain the transfer function, H(w) = 0 for the circuit below for R₁ = 1 kQ2, R2 = 10 kQ, and Vi C = 1 μF. What role, if any, does the capacitor play? Explain. R₁ R2 + C + Voarrow_forwardCORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE 3 (15 points): A 12-meter-long precast pile segment is to be lifted from a trailer down to the ground and then set in place prior to driving by a crane.1. If two slings are to be used in lifting the pile to the ground, at what distance from the ends must the slings be placed for minimum bending due to its own weight?2. At what distance from the ends must the slings be placed for minimum shear due to its own weight?3. Using one sling to set the pile in a vertical position before driving at what distance from one end must the sling be placed for minimum bending due to its own weight?ANSWERS: (1) 2.48 m, (2) 3.00 m, (3) 3.51 marrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
